【代码随想录+力扣hot100】双指针
文章目录
- 27. 移除元素
-
-
- 思路:
- 代码:
-
- 26. 删除有序数组中的重复项
-
- 代码:
-
- 思路一:重复元素必相邻
- 思路二:从第一个位置开始考虑快慢指针
- 977.有序数组的平方
-
-
- 思路:
- 代码:
-
- 283. 移动零
-
- 代码:
-
- 思路1:直接快慢指针
- 思路2:1次遍历(快排)
- 844.比较含退格的字符串
-
- 代码:参考题解理解
-
- 思路一:从后向前双指针
- 思路二:模拟栈
- 344.翻转字符串
-
-
- 代码:
-
- 151. 反转字符串中的单词
-
- 代码:
-
- 思路一:
- 思路二:
- 206.反转链表
-
-
- 思路:
-
- 19. 删除链表的倒数第 N 个结点
-
-
- 思路:
-
- 面试题 02.07. 链表相交
-
-
- 思路:
- 代码
-
- 142.环形链表II
-
-
- 思路:
- 代码:
-
- 15. 三数之和
-
-
- 思路:双指针
- 代码:
-
- 18. 四数之和
-
-
- 思路:
- 代码:
-
- 11. 盛最多水的容器
-
-
- 思路:
- 代码:
-
- 42.接雨水
-
-
- 思路一:单调栈(没看)
- 思路二:接雨水
- 代码:
-
27. 移除元素
思路:
快指针依次向后移动。
当遇到满足条件的情况时,快指针给慢指针赋值,慢指针向后移动一个位置,相当于指向了下一次要复制的地方,所以slow的位置是有效数据的后一个,如有效数据为2时,slow=2,前面0,1位置的数组有有效数据。slow=len。
代码:
class Solution {
public int removeElement(int[] nums, int val) {
int slow=0;
for(int fast=0;fast<nums.length;fast++){
if(nums[fast]!=val){
nums[slow]=nums[fast];
slow++;
}
}
System.out.println(slow);
return slow;
}
}
26. 删除有序数组中的重复项
代码:
思路一:重复元素必相邻
则慢指针slow从0开始,快指针fast从1开始,每次slow和fast进行判断。
如果slow和fast相同,说明重复,此时fast向右移动。
如果slow和fast不相同,说明不重复,则把fast位置的值赋值给slow+1的位置,之后slow和fast同时向右移动,再比较新的slow和fast是否重复。
则最后slow会移动到有效数组的最后一位,一共有slow+1个有效数字
如图:

class Solution {
public int removeDuplicates(int[] nums) {
int slow=0;
// 重复元素一定相邻
for(int fast=1;fast<nums.length;fast++){
if(nums[fast]!=nums[slow]){
nums[slow+1]=nums[fast];
slow++;
}
}
return slow+1;
}
}
思路二:从第一个位置开始考虑快慢指针
以112为例,slow fast从1开始,也就是从第二个1开始考虑
第一个循环fast=1(
所以相当于slow一直指向有效数据的后一个位置,代表slow是数组的长度
class Solution {
public int removeDuplicates(int[] nums) {
int slow=1;
for(int fast=1;fast<nums.length;fast++){
if(nums[fast]!=nums[fast-1]){
nums[slow]=nums[fast];
slow++;
}
}
return slow;
}
}
977.有序数组的平方
思路:
双指针左右计算谁的平方大,大的放入新数组,指针向左或向右移动。
注意:边界计算应包括left==right
代码:
class Solution {
public int[] sortedSquares(int[] nums) {
int left=0;
int n=nums.length;
int right=n-1,id=n-1;
int[] res = new int[n];
while(left<=right){
int l=nums[left]*nums[left];
int r=nums[right]*nums[right];
if(l<=r){
res[id--]=r;
right--;
}else{
res[id--]=l;
left++;
}
}
return res;
}
}
283. 移动零
代码:
思路1:直接快慢指针
非零赋值给slow的位置,后面位置用0填充
class Solution {
public void moveZeroes(int[] nums) {
int slow=0;
for(int fast=0;fast<nums.length;fast++){
if(nums[fast]!=0){
nums[slow]=nums[fast];
slow++;
}
}
for(int i=slow;i<nums.length;i++){
nums[i]=0;
}
// return nums;
}
}
思路2:1次遍历(快排)
这里参考了快速排序的思想,快速排序首先要确定一个待分割的元素做中间点 x,然后把所有小于等于 x 的元素放到 x 的左边,大于 x 的元素放到其右边。
这里我们可以用 0 当做这个中间点,把不等于 0(注意题目没说不能有负数)的放到中间点的左边,等于 0 的放到其右边。
这的中间点就是 0 本身,所以实现起来比快速排序简单很多,我们使用两个指针fast 和 slow,只要 nums[fast]!=0,我们就交换 nums[fast] 和 nums[slow]
请对照动态图来理解:

class Solution {
public void moveZeroes(int[] nums) {
int slow=0;
for(int fast=0;fast<nums.length;fast++){
if(nums[fast]!=0){
int temp=nums[slow];
nums[slow]=nums[fast];
nums[fast]=temp;
slow++;
}
}
}
}
844.比较含退格的字符串
代码:参考题解理解
题解链接 力扣
思路一:从后向前双指针
当然还可以有使用 O(1) 的空间复杂度来解决该问题。
同时从后向前遍历S和T(i初始为S末尾,j初始为T末尾),记录#的数量,模拟消除的操作,如果#用完了,就开始比较S[i]和S[j]。

class Solution {
public boolean backspaceCompare(String S, String T) {
//设置两个指针的位置,定义跳过次数机会变量
int i = S.length() - 1, j = T.length() - 1;
int skipS = 0, skipT = 0;
while (i >= 0 || j >= 0) {
//现在可以看成i后面的都是与j后面的一样,此时i往前面寻找下一个要比较的数,看看是否和j等等要找的数字一样
while (i >= 0) {
//如果i是井号跳过次数+1,就不用拿井号前面那个数字比较,通过这个循环来找下一个比较的数
if (S.charAt(i) == '#') {
skipS++;
i--;
} else if (skipS > 0) {
skipS--;
i--;
}
//如果找到了下一个要比较的数字,那你就break,去看看指针j怎么找的
else {
break;
}
}
//此时j往前面寻找下一个要比较的数,看看是否和i刚刚要找的数字一样
while (j >= 0) {
if (T.charAt(j) == '#') {
skipT++;
j--;
} else if (skipT > 0) {
skipT--;
j--;
} else {
break;
}
}
//如果i和j没越过边界,那就看看i,j所指向的值是否相等
if (i >= 0 && j >= 0) {
//不等返回false
if (S.charAt(i) != T.charAt(j)) {
return false;
}
}
//这里能够进去代表i或者j有一个或者两个越界了,
//那什么情况会进入?假如现在你的i和j后面的数字都比较过了,都是相等的‘
//但如果i找不到下一位的时候,找不到了,并且j能够找到下一个要比较的数字的时候,就证明两个数组不相等,返回false
else {
if (i >= 0 || j >= 0) {
return false;
}
}
i--;
j--;
}
return true;
}
}
思路二:模拟栈
class Solution {
public boolean backspaceCompare(String s, String t) {
StringBuilder ssb = new StringBuilder();
StringBuilder tsb = new StringBuilder();
for(char c:s.toCharArray()){
if(c!='#'){
ssb.append(c);
}else if(ssb.length()>0){
ssb.deleteCharAt(ssb.length()-1);
}
}
for(char c:t.toCharArray()){
if(c!='#'){
tsb.append(c);
}else if(tsb.length()>0){
tsb.deleteCharAt(tsb.length()-1);
}
}
return ssb.toString().equals(tsb.toString());
}
}
344.翻转字符串
代码:
class Solution {
public void reverseString(char[] s) {
int left=0;
int right=s.length-1;
while(left<right){
char temp=s[left];
s[left]=s[right];
s[right]=temp;
left++;
right--;
}
// return
}
}
151. 反转字符串中的单词
代码:
思路一:
用库
class Solution {
public String reverseWords(String s) {
String[] s1=s.split(" ");
StringBuilder stringBuilder = new StringBuilder();
for(int i=s1.length-1;i>=0;i--){
// System.out.println(s1[i]);
if(!s1[i].equals("")){
stringBuilder.append(" " + s1[i]);
}
}
return stringBuilder.toString().trim();// 去除空白
}
}
思路二:
双指针实现
class Solution {
public String reverseWords(String s) {
char[] chars = s.toCharArray();
//1.去除首尾以及中间多余空格
chars = removeExtraSpaces(chars);
//2.整个字符串反转
reverse(chars, 0, chars.length - 1);
//3.单词反转
reverseEachWord(chars);
return new String(chars);
}
public char[] removeExtraSpaces(char[] chars) {
int slow=0;
for(int fast=0;fast<chars.length;fast++){
//先用fast移除空格
if(chars[fast]!=' '){
//再用slow加空格,除第一个单词外,单词末尾要加空格
//手动控制空格,给单词之间添加空格。slow != 0说明不是第一个单词,需要在单词前添加空格。
if(slow!=0){
chars[slow++]=' ';
}
// fast遇到空格或遍历到字符串末尾,
//补上该单词,遇到空格说明单词结束。
// while(chars[fast]!=' '&&fast
while(fast<chars.length&&chars[fast]!=' '){
chars[slow++]=chars[fast++];
}
}
}
char[] newChars = new char[slow];
System.arraycopy(chars,0,newChars,0,slow);//把chars的元素复制给newchars 长度为slow
return newChars;
}
//双指针实现指定范围内字符串反转,可参考字符串反转题解
public void reverse(char[] chars,int left,int right){
while(left<right){
char temp=chars[left];
chars[left]=chars[right];
chars[right]=temp;
right--;
left++;
}
}
public void reverseEachWord(char[] chars){
int slow=0;
//end <= s.length() 这里的 = ,是为了让 end 永远指向单词末尾后一个位置,这样 reverse 的实参更好设置
for(int fast=0;fast<=chars.length;fast++){
// end 每次到单词末尾后的空格或串尾,开始反转单词
if(fast==chars.length||chars[fast]==' '){
reverse(chars,slow,fast-1);
slow=fast+1;
}
}
}
}
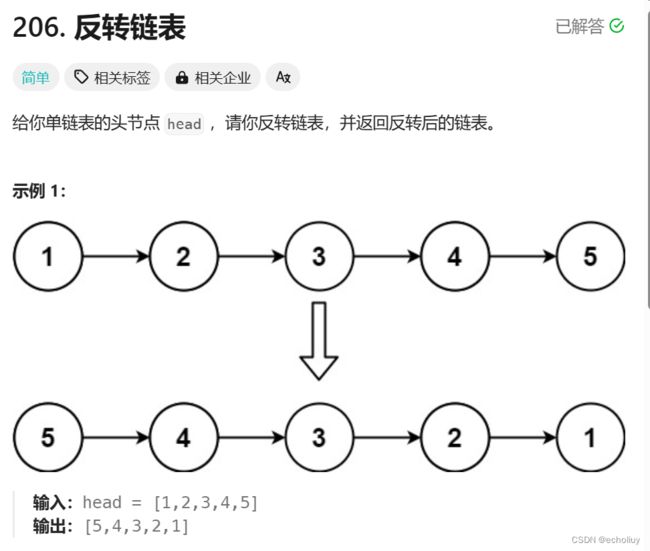
206.反转链表
思路:
注意:先把cur赋值给p,再把cur.text赋值给p。则,在cur≠null的最后一个位置时,p移动到了cur的位置,cur移动到了null,此时循环终止。则p成为了链表的新head。
class Solution {
public ListNode reverseList(ListNode head) {
ListNode cur=head;
ListNode p=null;
while(cur!=null){
ListNode temp=cur.next;
cur.next=p;
p=cur;
cur=temp;
// p=cur;
}
return p;
}
}
19. 删除链表的倒数第 N 个结点
思路:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy=new ListNode(0,head);
ListNode fast=dummy;
ListNode slow=dummy;
for(int i=0;i<=n;i++){
fast=fast.next;
}
while(fast!=null){
fast=fast.next;
slow=slow.next;
}
slow.next=slow.next.next;
return dummy.next;
}
}
面试题 02.07. 链表相交
思路:
代码
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode a=headA;
ListNode b=headB;
while(a!=b){
if(a!=null){
a=a.next;
}else{
a=headB;
}
if(b!=null){
b=b.next;
}else{
b=headA;
}
}
return a;
}
}
142.环形链表II
思路:
-
判断链表是否有环
可以使用快慢指针法,分别定义 fast 和 slow 指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环。
-
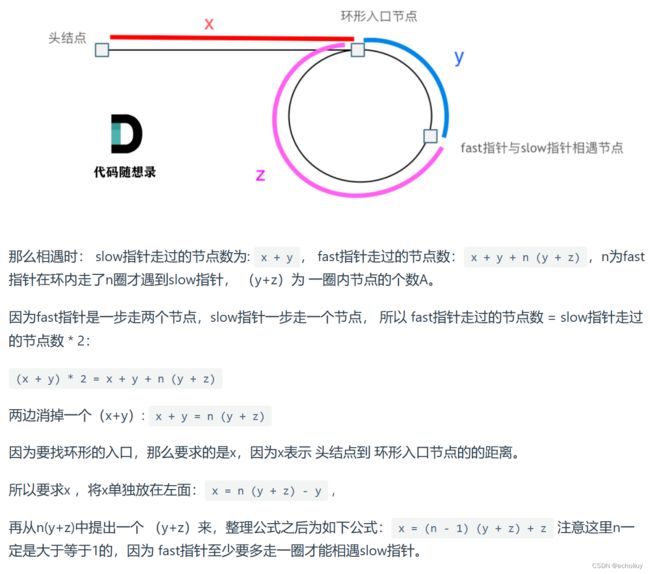
如果有环,如何找到这个环的入口
先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了。
当 n为1的时候,公式就化解为 x = z,
这就意味着,从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是 环形入口的节点。
也就是在相遇节点处,定义一个指针index1,在头结点处定一个指针index2。
让index1和index2同时移动,每次移动一个节点, 那么他们相遇的地方就是 环形入口的节点。
代码:
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast=head;
ListNode slow = head;
//设快指针是慢指针速度的2倍
// while(fast!=slow){
// 循环条件是fast没走到空
while(fast!=null&&fast.next!=null){
fast=fast.next.next;
slow=slow.next;
//如果快慢指针相遇了,说明有环
if(fast==slow){
ListNode index1=head;
ListNode index2=fast;
while(index1!=index2){
index1=index1.next;
index2=index2.next;
}
return index1;
}
}
return null;
}
}
15. 三数之和
思路:双指针
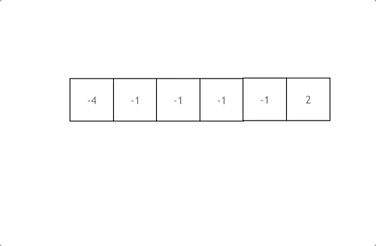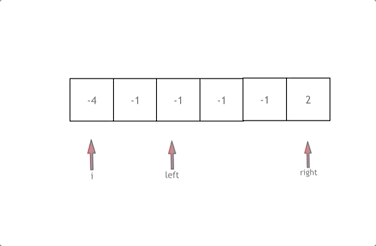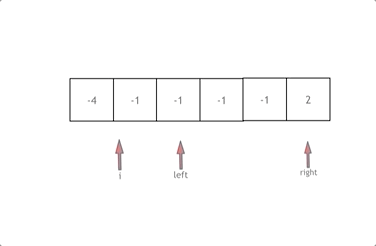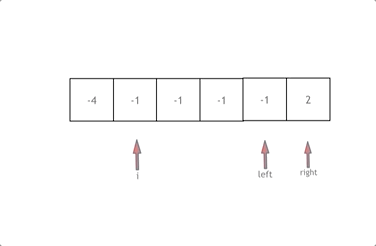
拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
时间复杂度:O(n^2)。
代码:
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
// 三元组 ijk
// List result = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
// 对数组重新排序,可以使用双指针
Arrays.sort(nums);
for(int i=0;i<nums.length;i++){
// 去重
// while(i0&&nums[i]==nums[i-1]){
// i++;
// //应该跳过这次循环
// // continue;
// }
if(i>0&&nums[i]==nums[i-1]){
continue;
}
int left=i+1;
int right=nums.length-1;
while(left<right){
int sum=nums[i]+nums[left]+nums[right];
if(sum==0){
result.add(Arrays.asList(nums[i],nums[left],nums[right]));
//left right去重
while(left<right&&nums[left]==nums[left+1])left++;
while(left<right&&nums[right]==nums[right-1])right--;
//如果找到了向内收缩
right--;
left++;
}else if(sum<0){
left++;
}else{
right--;
}
// //left right去重
// while(left
// while(left
}
}
return result;
}
}
18. 四数之和
思路:
ij left right四个指针。考虑外部两层的去重。
代码:
注意:j循环和i循环是都是在第一个初始值的后面去判断 前一个和后一个的区别。
同时,因为数组是增长的,所以可以对i直接做剪枝。
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
for(int i=0;i<nums.length;i++){
// 因为数组递增,所以如果数组大于目标值而且已经为正数的话,后面不用计算了
// 没有这个循环会超时
if(nums[i]>target&&nums[i]>0){
return res;
}
// 去重
if(i>0&&nums[i]==nums[i-1]){
continue;
}
for(int j=i+1;j<nums.length;j++){
if(j>i+1&&nums[j]==nums[j-1]){
continue;
}
int left=j+1;
int right=nums.length-1;
while(left<right){
int sum=nums[i]+nums[j]+nums[left]+nums[right];
if(sum==target){
res.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right]));
//left right去重
while(left<right&&nums[left]==nums[left+1])left++;
while(left<right&&nums[right]==nums[right-1])right--;
//如果找到了向内收缩
right--;
left++;
}else if(sum<target){
left++;
}else{
right--;
}
}
}
}
return res;
}
}
11. 盛最多水的容器
思路:
代码:
class Solution {
public int maxArea(int[] height) {
int left=0;
int right=height.length-1;
int s=0;
while(left<right){
// s=Math.max(s,(right-left)*Math.min(height[left],height[right]));
//短板收缩
if(height[left]<=height[right]){
s=Math.max(s,(right-left)*height[left]);
left++;
}else{
s=Math.max(s,(right-left)*height[right]);
right--;
}
}
return s;
}
}
42.接雨水
思路一:单调栈(没看)
思路二:接雨水
灵神题解
代码:
class Solution {
public int trap(int[] height) {
int length = height.length;
if (length <= 2) return 0;
int[] maxLeft = new int[length];
int[] maxRight = new int[length];
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i< length; i++) {
maxLeft[i] = Math.max(height[i], maxLeft[i-1]);
// System.out.println("左边柱子"+maxLeft[i]);
}
// 记录每个柱子右边柱子最大高度
maxRight[length - 1] = height[length - 1];
for(int i = length - 2; i >= 0; i--) {
maxRight[i] = Math.max(height[i], maxRight[i+1]);
// System.out.println("边右柱子"+maxRight[i]);
}
// 求和
int sum = 0;
for (int i = 0; i < length; i++) {
int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
// System.out.println(i+":left:"+maxLeft[i]+"Right"+maxRight[i]+"-height"+height[i]+"--countt:"+count);
if (count > 0) sum += count;
}
return sum;
}
}