【深度视觉】第三章：卷积网络诞生前：卷积、边缘、纹理、图像分类等

五、卷积网络诞生前：卷积、边缘、纹理、图像分类、卷积核的设计等

前面第一章里面，已经讲过一点机器视觉的诞生史，但那都太久远，我觉得非常有必要把近期视觉发展的研究成果，也聊清楚，这对深入理解卷积网络是如何工作的非常有意义。

在计算机视觉中，我们要处理图片就意味着，我们只要改变像素的取值即可改变图片。而如果我们要让计算机从图片中获取人类的语义信息，就需要计算这些图片的数字，并从中发现和提取数值规律，来解释和跨越人类和计算机之间的“语义鸿沟”，也就是要建立从像素到语义的映射关系。

而这个问题的难点在于：比如视角、光照、尺度、遮挡、形变(几何性变)、背景杂波(比如白色北极熊在北极)、类内变形(不同的椅子)、运动模糊、类别繁多。

当时的解决方法是从人类的视角驱动的范式，比如基于规则的分类方法，就是通过硬编码的方式，抽取图像的一些特征，用这些特征和目标进行匹配。比如抽取GIST特征(就是一个频率的特征)、边缘检测(边缘特征)、角点等关键点特征去对比来做识别。这就是传统视角的研究内容。这部分内容你看我的博客 宝贝儿好-CSDN博客 中的opencv系列就可以有非常深入的理解了。直到深度学习出现，才出现了以数据驱动的图像分类范式，比如机器学习、深度学习，就是通过数据找规律。

1、卷积计算的诞生史

在深度学习之前，科研工作者就已经积累了大量的图像处理技术，比如调节明暗度、对比度、饱和度等，比如进行几何变形，比如提取图像中的线条、边缘、轮廓等，比如提取图像中的关键点、角点、特征点等，比如上下采样、直方图、傅里叶变换、求梯度等等非常非常多的、非常非常巧妙的图像处理技巧。这些在我的opencv里面都有详细通俗的介绍，你看完后会有会心一笑的释怀，也会惊叹科研工作者们在跨越语义鸿沟做出的各种努力。

其中，在科学家研究如何检测图像边缘这一任务时，科学家们想了很多方法，其中最常用的一个方法就是用图像梯度来做边缘检测。比如自动驾驶里面，我们至少要做的一个工作就是道路的边缘检测，只有正确的检测到道路的边缘我们的车才会行驶在道路上而不是开到马路牙子外。或者从另一个角度解释，我们做边缘检测不是让人眼去欣赏一张道路图片里面的道路边缘的，我们正确检测出一张图像的边缘是为了让模型更好的去认识这张图片中的道路。所以精确的边缘检测可以帮助模型很好的识别这是道路还是道路外面，从而做出正确的反馈——指导汽车正确行使。也所以边缘研究是非常重要的，边缘是跨越图像语义的第一步。

就是当我们匹配出物体的边缘，基本是个什么物体我们就大致知道了：

上图中，我们只要抓取图像中的边缘，这种少数像素点，就可以知道图像是什么意思，第一张图就是一个人，而且还是位女士，第二张图就是一个瓶子。
此外，我们还对边缘进行分类，分类的目的就是为了更加细节的提取图像的语义信息。比如对于瓶子，我们重点提取的就是表面法向不连续的边，对于颜色不连续、光照不连续我们就可以忽略，也可以知道这就是一个瓶子。当然如果我们想知道这个瓶子是否在桌面上，那我们就要重点看光照不连续的边，因为这个边可以让我们判断瓶子是否在桌面上。比如对于左边的女士，我们提取到眼睛鼻子嘴巴就大概率是个动物吧。

这就是边缘，而对边缘的检测，最早的就是用图像梯度来做边缘检测。

下面我们看看图像梯度计算的数学过程：

A处是微积分中的梯度计算公式。它的几何意义就是，当自变量x或者y在各自的方向上改变一点点，函数值z随之改变了多少。导数值不仅表示大小还有方向的意思。当我们把导数的概念引入图像处理中，我们就简化成当公式B：像素点在x轴或者y轴跳动一步，就是移动一个像素点，我们像素值的改变量，在计算机视觉领域我们把这个改变量叫做梯度。
而这个梯度可视化后就是C图，C图的第一行是图片的像素数据，黄色就是每个像素点的梯度值。而这个梯度值说白了，它就是图像中左右像素点或者上下像素点之间的差值嘛，就是做了个差分而已。但是这个差值是有意义的！你看，梯度值越大就表示这个像素点左右或者上下像素之间的差值越大，而差值越大越说明这个像素点是图像中的边缘信息。所以，我们提取了图像中的梯度，就是提取了图像的边缘，就是达到了图像边缘检测的任务目标了！那我们只要把差值大于某个阈值的像素点都留下来，把小于阈值的像素点都变0，不就是是一张只有图像边缘的图片了嘛，真是美哉。后来鼎鼎大名的Canny边缘检测就是一种一阶微分算子检测算法。

这里想再强调一下的是，图像的梯度除了有大小(差值)，还有方向的：

上面的差分求导也可以用卷积操作来完成：

但是，人们又发现一个问题，这种相邻像素之间做差分的做法太粗暴，也不考虑一下周边近邻像素的影响。于是人们又想出了卷积计算，就是把临域像素也考虑进来，用各式各样的卷积核kernel对原图像进行卷积操作，其中最著名的是sobel算子、scharr算子、laplacian算子。这里抛砖引玉，就只看一下sobel算子：

哇！这不就是卷积核和卷积计算嘛！是滴！而且有没有发现，它的计算其实就是两个矩阵对应位置相乘再加和嘛，这是不是还非常符合GPU底层的计算逻辑！所以卷积操作有了硬件的加持，就更香了。那时的人们就是削尖脑袋想怎么设计出更牛、更强的卷积核来提取图像中更高级的语义，已经不满足只提取边缘了。所以你学了opencv后，你会发现那时期出现了各式各样款型的卷积核，当然那时还不叫卷积核，那时叫滤波器，因为这个计算逻辑是从物理学中引进的，但也有叫算子的，因为这个卷积核在数学中人们一般称为算子，而图像工作者更愿意称它为模板，因为这个称呼是传统图像研究的思路。所以那时出现了高通滤波、低通滤波、均值滤波，方框滤波，高斯滤波，中值滤波，双边滤波。。。一时间滤波器满天飞。。。关于滤波核的性质、特点等也是总结了很多结论，下面简单展示几个重要的知识点，我认为这些都是非常有助于你以后理解卷积网络本质的点：

（1）简单滤波核展示：

可见，除了边缘提取，还有去噪、平移、平滑、锐化、纹理表示等等神奇的效果。但是上面的卷积核还是太简单，后面人们就重点开始研究高斯滤波核：

（2）高斯滤波核

这里重点把高斯滤波核单独拿出来讲，不仅是因为高斯核可以根据邻域像素与中心点的远近程度分配权重，而且高斯滤波核还有其他一些很牛掰的性质：

• 如何生成高斯核

生成高斯核的计算公式自然就是二元正态分布公式。要生成高斯核，首先要确定你想生成什么尺寸、以及标准差是多少，比如上图的5x5尺寸、标准差=1的高斯核，就是一个5行5列的数组，数组中的数字按行、按列都是标准差=1，那最中间的那个位置的坐标就是(0,0)，把(0,0)当作x,y，把标准差=1，带入高斯公式，就得到中间位置的数值了。同理，以中间位置为坐标原点，向右向上是正方形，把各个位置的坐标和标准差带入就得到各个位置上的数值了。最后一步就是一定要记得对所有权重进行归一化。一定要归一化，否则所有行所有列之和大于1或者小于1，卷积出来的图像要么是全白的，要么是都黑了一个度，这是不行的。只有归一化后，我和我周围的像素卷积后，才不会改变像素的范围。

• 不同的高斯核尺寸、标准差对卷积效果的影响：

可见：
相同尺寸的情况下，方差越大的卷积核，卷积操作后，对图像的平滑就越厉害；方差越小的卷积核对图像平滑就轻微。因为方差越小，说明数据越集中，那中间的数值分布就越多，中间的值就越大，中间值越大卷积时，中间像素点的权值就越大，周围像素点的权值就越小，那卷积后每个像素的值就越和自己原来的值相似。总之，一句话，方差越大，平滑效果越明显。

方差相同尺寸不同时：方差相同就表示两个核的所有位置上的数值大小是一样的，但是高斯核最后一步是归一化，所以当你核的尺寸较大时，归一化后所有数值就相对变小了。所以方差相同，尺寸越大平滑效果越明显，尺寸越小平滑效果越轻微。

小结：大方差或者大尺寸卷积核的平滑能力强；小方差或者小尺寸卷积核平滑能力弱；

经验法则：将卷积核的半窗宽度设置为3δ，最终卷积模板尺寸为2x3δ+1。例如：标准差设置成1，卷积模板宽度=2x3x1+1=7。
因为正态分布中，约有99.7%的数据分布在均值±3σ的范围内，就是说如果一组数据符合正态分布，那么大约有99.7%的数据将位于平均值左右6σ的范围内。所以当我们这样设计的卷积核，都几乎不用归一化了，所有数字之和都几乎是1了。而且超过±3σ范围后，计算出来的数值都几乎是0了，大量黑边的卷积核，黑边也没有什么意义的。

高斯卷积核的意义：去除图像中的“高频”成分(低通滤波器)。图像中的噪声、边缘都是高频。所以高斯卷积核是过滤高频信号，让低频信号通过，所以也叫低通滤器。

• 高斯卷积核的性质：两个高斯卷积核卷积后得到的还是高斯卷积核。

使用多次小方差卷积核连续卷积，可以得到与大方差卷积核相同的结果。
使用标准差为δ的高斯核进行两次卷积，与使用标准差为√2δ的高斯核，进行一次卷积相同。
一个二维的高斯核可以分解成两个一维高斯核的操作。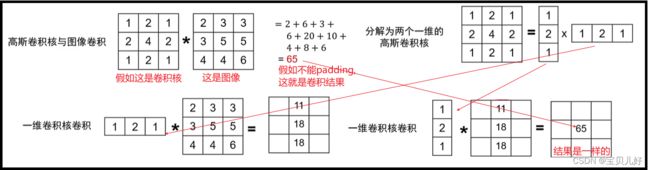

这种拆解的意义就在于可以降低计算复杂度。如果做一次乘法就是一次计算，那么一个mxm卷积核卷积操作一次的计算量就是m^2,如果对一个nxn的图像进行卷积，那计算复杂度就是O(n^2 * m^2)。如果把mxm卷积核分解成两个m卷积核，计算复杂度就是O(n^2 * m)。计算量降低了很多。
所以后面我们学卷积网络的时候，可以把大卷积核，比如5x5的卷积核，拆解为两个小卷积核，比如两个3x3的卷积核，做两次卷积操作，其效果是一样的，但计算量就下降很多。
而且我们还可以把比如7x7的卷积核直接拆解成两个1x7和7x1的卷积核，计算量就更低了。

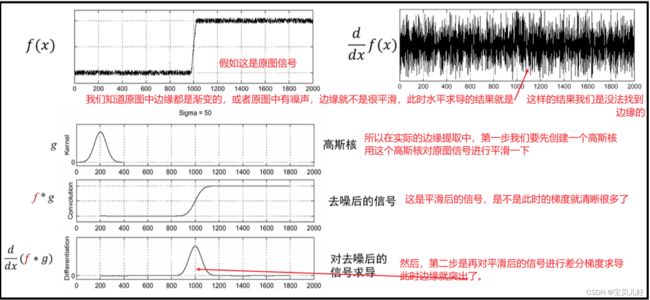
• 高斯一阶偏导卷积核

在实际的边缘提取中，我们都是按照上述两步骤来操作的。但是上面两步都是可以通过卷积核进行卷积操作完成的。而且卷积核的卷积操作又有结合性和交换性，所以上面的步骤我们可以一步到位：

上图中间的模板就叫高斯一阶偏导模板，就是说我们可以先把这个模板做好，然后图像信号来了，直接用这个模板卷积图像信号就可以提取图像的边缘了，这样更快。所以高斯偏导模板集平滑功能和求导(差分)功能于一身。下面可视化看看这个模板：

高斯一阶偏导核如何生成？自然是先人为指定标准差δ了，然后通过2x3δ+1确定窗口尺寸，然后通过二元高斯函数生成各个数值，然后再归一化，然后再水平求导(差分)就是垂直方向上的核了，如果垂直方向求导就是水平方向上的边缘核了。
所以，高斯一阶偏导核也就是只有一个超参数δ，下面我们看看δ是如何影响边缘信息的提取的：

可见，方差越小提取的边缘信息越清晰；方差越大，边缘的细节信息越不清，提取的都是轮廓的边缘信息了。
所以，我们可以通过调整模板方差来提取图像的不同信息。如果我们想提取人的轮廓信息，就用大方差的高斯偏导核；如果我们想提取人脸的眼睛鼻子眉毛等细节信息就用小方差的高斯偏导核。

小结高斯核：
消除高频成分，所以也叫低通滤波器。
卷积核中的权值不可为负数。
权值总合为1，恒定区域不受卷积影响。

小结高斯一阶偏导核：
高斯核的导数。
卷积核中的权值可以为负。
权值总合是0，恒定区域无响应。
高对比度点的响应值大。

此时，你再去理解大名鼎鼎的Canny边缘检测就不难理解了，详细步骤参考我的opencv系列中专门有一个章节讲Canny边缘检测。

至此，以上都是卷积操作的一系列研究成果。迈向跨越语义鸿沟的第一步：边缘检测，我们是已经做到了很好，继续往前走就是纹理表示。一个物体之所以是这个物体就是它自己独特的纹理，比如人脸之所以是人脸，是因为它有自己独特的、固定的眼睛鼻子嘴巴等这些基元。而纹理也是分类的前奏。所以下一步开始研究纹理。

2、纹理基元

不管是规则纹理还是生活中的随机纹理，我都可以将纹理看出物体的特有的特征或者属性。物体和物体之所以不同，很大程度上就是因为不同的物体拥有不同的纹理基元。比如上图2中的点点就是一种纹理基元，上图6中的横条纹也是一种纹理基元，那我们如何能提取这些不同的基元呢？只有提取到不同的基元，是不是就可以根据不同的基元进行物体分类了！

• 纹理基元的表示

前面讲边缘的时候，说过不同的卷积核可以提取不同方向的边缘，那我是不是可以用一组卷积核来表示某种基元？于是基于卷积核组的纹理表示方法诞生了：

最开始我们是上图A中的方法，使用的都是一个卷积核来提取特征。凡是在原图中，上下垂直方向的梯度变化很大的区域，经过这个卷积核卷积后，这个区域的响应值就很大。也就是一个核只能提取和它对应的特征，那我是不是可以制作一组卷积核，提取一组的特征？！对，就是B图，人们设计了一组卷积核，其中前六个核都是各个方向的高斯一阶偏导核，第七个核是斑点或者圆形基元的模板。我们现在用这一组卷积核分别对原图进行卷积，这样就提取了原图的七种特征！此时生成的特征图就是(7,原图像素个数)这样的一个数据，可以说这个数据就是提取了原图7种不同特征后的7个特征图数据。比如第一张特征图r1，就是重点响应原图中有没有水平边缘的特征图。上图中我们红框框住的地方就是水平线明显的地方，那特征图r1也是在响应位置有较大数值，而其他位置由于没有很大的响应，数值就很小。同理其他特征图。 此时这个(7,原图像素个数)就表示我们提取了原图中的和模板匹配的纹理信息了，而且纹理的相对位置都是一一对应的。

但是，这样的特征表示结果也太大了，数据不好处理。而且我也只是想提取不同的特征，也没必要去记住这些特征在原图中的位置信息，我只需要关注哪种基元对应的纹理，以及这种纹理出现的频率即可，所以此时我们就可以用每个特征图的均值来表示这个特征即可，就是C图。这就大大简化了数据量，我们只要7个数值就表示原图的7个特征！我们就可以根据特征进行分类了！比如上图C中，如果r1横的值比较大，就说明原图中有大量的水平边，如果r4横大，就说明原图中有大量的垂直边。所以我们只要这7个向量就可以表示原图了。

如果还不理解，就看下图再理解一遍：

上图的纹理表示ABC都是均值的结果，就是分别有7个元素的三个数组。以图像1为例，图像1里面的基元都是圆点，所以这样的基元只有第七个卷积核对它有响应，其他卷积核几乎没响应，所以这组卷积核组卷积完毕得到的7个均值数组中，就只有第七个卷积核的结果是最大的，所以第7个均值最大，就是最亮的，所以纹理表示C数组就是图像1的卷积结果。其他图像同理。

可见：
左边的纹理是我们人类的识别逻辑，右边的纹理表示(一组向量)就是计算机的识别逻辑，我们把人类的语义和计算机的数值映射起来了。也是我们用数字把纹理表示出来了。
这个卷积核组的思路就是：利用卷积核组提取图像中的纹理基元；利用基元的统计信息来表示图像中的纹理。
也可以说，利用卷积核组对图像进行卷积操作，获得了对应位置的特征响应，这些特征响应构成了特征响应图。然后我们再利用这些特征响应图的某种统计信息来表示图像中的纹理。
更粗暴的说，就是我们用卷积核组提取了图像的特征；用特征的统计信息表示了图像。

纹理基元是一个物体和其他物体不同的基本元素！我们人类可以根据不同的基元进行物体与物体之间的分类。那计算机就可以根据特征的统计信息进行分类了。
我们把人类认识的基元和计算机认识的特征统计关联起来了，就是将基元和特征统计之间建立了映射，此时计算机的分类就可以帮助人类分类了。

• 特征提取

上述提取图像特征的关键就在于如何设计很适合的卷积核组了。就是设计怎样的核尺寸、核方向，来检测图像中的边缘、条形以及点状等纹理基元。

上图的48个卷积核组就是，卷积网络架构诞生以前，我们人为设计的卷积核组。
这48个卷积核组中，检测边缘信息的有18个核，都是高斯一阶偏导核，可以检测6个方向的边缘，而且可以有3种δ，就是可以检测3种粒度的边缘。
有18个检测条状基元的卷积核，也是有6种检测方向，有3种检测颗粒度。
有12个检测点状基元的卷积核，其中前8个检测的是中间暗周围亮的点状基元，后4个卷积核检测的中间亮周围暗的点状基元。

人们把这48个卷积核分别和原图进行卷积操作，就得到48张特征相应图，然后分别把这48张特征响应图求均值，就得到一个48维的向量，我们就可以用这个48维向量来表示原图了。

这里再解释一遍：如果暂时不考虑padding，那么可以说这48张特征图的数据个数是和原图是一样的！但是，这48张特征图中的0值非常多，是一个稀疏矩阵，因为假如原图中有一条水平线，那对这条水平线有响应的肯定只有上图最左侧的3个边缘核最敏感，其他核是不敏感的，所以只有那3个核有很大的响应。原图水平线位置上，被卷积48次后，只有3次是有强响应的，其他45次的响应都是几乎接近0。也所以当我们只想知道原图中是否有水平线这种基元的时候，我们只需用均值表示即可，也没必要用一个(48,原图像素点个数)这么大的一个稀疏矩阵来表示。

从这个角度看，你就不难理解后面我们将要学习的RNN的经典架构中，为什么都是卷积+池化的操作。如果说卷积都是提取特征的，那么池化是对特征进行统计的。所以RNN中的池化操作的重要性就类比于DNN中的激活层。

3、将深度学习引入图片分类领域
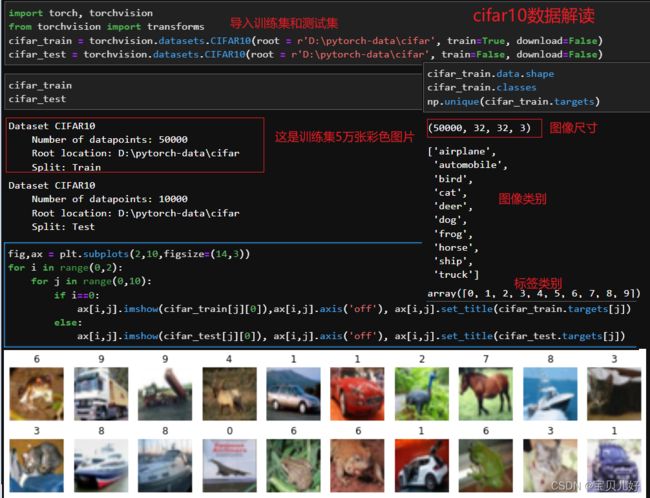
时间飞奔到2010年前后，深度学习大火了。就是前面我讲的DNN系列，全连接神经网络，就是它火了。图像研究学者自然也不会熟视无睹，把DNN引入图像分类，继续踏上跨越语义鸿沟的艰难历程。下面先给大家展示一下当时人们如何用DNN来对CIFA10数据集进行线性分类。

第一步：cifar10数据解读和加载

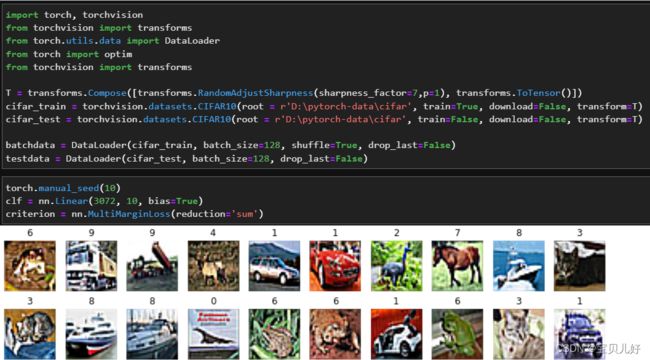
第二步：用DNN创建一个单层线性分类器:
这里并非是展示什么分类器强大，这里主要是串联一下卷积网络诞生过程中的一些重要节点，所以这里我用DNN建立一个单层的线性分类器：

第三步：确定损失函数：
上面我们已经创建了分类器，也就是当有一张图片X输入clf，正向传播后就有10个得分f。当我有一个batch张图片输入clf，正向传播后就有(batch,10)个输出，就是batch行10列的输出矩阵。

下面我们就需要一个损失函数，这个损失函数可以定量的度量模型的预测结果和样本标签之间的差异程度。而且这个损失函数还可以搭建模型性能与模型参数之间的桥梁，指导模型参数优化。更官方的话就是：损失函数是一个函数，用于度量给定分类器的预测值和真实值之间的不一致程度，其输出通常是一个非负实值。这个非负实值可以作为反馈信号来对分类器参数进行调整，以降低当前样本对应的损失值，提升分类器的分类效果。

所以以后我们自己创建损失函数的时候，一定要把握这两点：一是尽量输出的是非负实值，因为后续我们通常用的优化算法都是梯度下降法，如果你的损失函数是负值，是不是你的优化算法也得随之改动，不是不可行，而是后续很麻烦。二是损失函数除了能衡量模型输出和标签之间的差异程度外，还必须和模型参数有关，如果你的损失函数中没有模型参数，那这个损失就无法牵引模型学习和训练，那你的损失函数就是一个无效的、或者说不能用的损失函数，你得考虑其他损失函数。比如我们的分类任务，你也可以用准确率来衡量预测值和标签的差异啊，但为什么我们不用，就是因为它和模型参数无法关联。所以准确率只能是一个分类模型性能的评价指标，而不能作为一个损失函数来用。

所以损失函数的定义是下图左边的通用形式，也所以损失函数就是下图的L表示的，那L具体的表达式怎么写，就和你的数据、模型、任务有关了，所以以后我们会遇到各种不同形式的损失函数，到时你不要惊讶，其实都是理所当然的。

• 多类支撑向量机损失

这里我们是10分类任务，我先给大家展示用多类支撑向量机损失作为我们的损失函数的效果：

其实随着数据、模型、任务的不同，人们一直在探索适合自己的损失函数。比如针对多分类任务，多类支撑向量机损失是最开始人们通常采用的损失函数形式，但后面发现其实这个损失不是很完美，后面人们又发明了交叉熵损失。至于为什么它不完美、什么是交叉熵损失，我们后面还会展开讲。这里先展示一下支撑向量机损失，因为只有你非常了解了它，才知道为什么。

上图公式中的Sij是样本真是标签类别的分值，Syi是样本其他类别的分值。上图公式的几何表示在下图，因为上面实在放不下了，就加到下图。我们可以先看一下下图的hingeloss,其中横坐标就是样本的10个类别的分值坐标，纵坐标就是loss。Sij就是样本标签类别的分值，当样本其他类别的分值Syi小于Sij+1时，loss=0，当样本其他类别的分值Syi大于Sij+1时，就产生Sij+1-Syi的损失，所以图中的斜线是135度角的斜线。

A：上图右边的+1，学过SVM得都应该知道，就类似是决策边界的一个硬间隔。就是你这个样本点不能紧紧得落在我决策边界上，你至少要远离我决策边界1个单位，因为离决策边界越远，是某个类别的把握更大嘛，比如假如决策边界是猫，那落在决策边界上的样本是猫的概率可能就是0.6，离决策边界越远是猫的概率就越高比如0.9，那我当然是希望离决策边界越远越好了。当然这里的间隔我举例用的是1，你也可以设置为其他数值。

B：从损失函数的公式上看，如果样本的标签是猫，模型预测也是猫，而且这个样本离猫的决策边界也是大于1单位间隔的，那这条样本的损失就是0；
如果虽然模型预测也是猫，但硬间隔小于1，那就产生损失不到1的损失；
如果模型预测结果都不是猫，那这条样本的损失就至少是大于1的。如果你预测结果越离谱，损失就越大。

如果从公式看不懂的，可行看下图的示例和hinge loss的几何图来理解：

可见：
样本1压根就没分类正确，样本1的标签是鸟，但模型预测的是车，因为车的分值1.9最高嘛。所以它的损失算出来就是2.3。假设模型预测出车的分值是100，那这条样本的损失就是100-0.6+1=100.4，就更大了。
样本2虽然也分类正确了，但它还是有0.4的损失，因为它没有比2.3大够1，算出来就是0.4的损失。
样本3是预测正确了，而且硬间隔都大于1，所以损失是0。

hingloss在pytorch中也是有打包好的函数，我们可以通过torch.nn.MultiMarginLoss类实现，也可以直接调用F.multi_margin_loss函数。

说明：pytorch的hingloss计算公式比我们的公式多了一个分子，就是多除了一个标签类别数。其实这个不影响，都一样。

第四步：确定优化算法
参数优化和损失函数都是深度学习中的核心环节。参数优化就是利用损失函数的输出值作为反馈信号来调整模型参数，以提升模型对训练样本的预测性能。优化算法的目标是找到使损失函数L达到最优的那组参数w。
最直观的理解是：损失函数L=0对应的那组w就是最优的一组参数，但是实际中几乎很难能求出L=0的那组参数。如果我们能写出L对w的导数的显性表达式，然后令L对w的导数=0，就也可以解出L最小值对应的那组w。这也是最小二乘法的思路。
但是实际中我们也是常常写不出L对w的导数的显性表达式，所以我们通常的做法是：就先随机选择一组w，然后让L对w的导数=0，求出在当前w下，L减小的方向，然后更新w，让L逐渐逼近它的最小值，这就是深度学习中最常用的一阶梯度下降算法————迭代优化方法。

这里我们就用带动量法的小批量梯度下降算法：

动量法我们在这里不展开聊了，后面会针对优化算法专门写一个标题。

第五步：训练模型

一开始训练我发现是怎么训练准确率都提升不上去，一直在百分之二三十附近，就相当于瞎猜，后来我就做了数据增强。由于这个分类器实在不给力，想来想去觉得也是图像不清晰，所以只做了锐化增强。而且我现在的情况是严重欠拟合，所以像裁剪、翻转、形变等增强技术都不在我现在的考虑范围内。而且一开始用的优化器是SGD+手动分阶段调整学习率和动量值，发现很难优化，后来也改成更强大的优化器RMSprop,后又改成adam，一系列优化后，发现训练集的准确率只有一次最高突破了45%！！等于就没有训练成这个模型。后面如果还想继续训练，得从数据下手继续做特征工程，，，这个问题先搁置吧，因为后面我们的案例都以这个数据集为例，后面还会展示其他更强大的分类器。其实这里主要是说明下面两点的：

（1）看线性分类器权值向量：
上面我的模型就没有训练出来，所以我可视化权值后几乎看不到规律，下面是鲁鹏老师ppt的结果，我们看他的结果吧：
把所有的w都归一化到(0, 255)之间，看看w是何物：

当时人们给w都叫模板，可见这些模板和图像长得非常相似。所以，这些模板是不是都是记录了这些类别的信息，就是记录了数据库里面每种类别的统计信息。背后的数学是：

x就是图像，w就是模板，当x和w很像的时候，x和w的点积就会非常大，正向传播后输出值就越大，那这个x就是w模板对应的类别。所以从这个角度说，模板记录的就是图片的统计信息：平均值。尤其是看类别8，类别8是马，这里马有两个头是因为图片库里面有的马朝左有的朝右，所以模板记录的信息就是左右两个马头。也所以，线性分类器的作用就是：输入一个图像x，把x和10种模板w都点乘一下，看和哪个模板点乘的结果最大，就是哪种类别。也就是看输入图像与模板的匹配程度，越匹配输出的结果就越大。

（2）看决策边界：
线性分类器的本质就是寻找决策边界，我们的图像是有3072个特征，也就是3072维度，这个维度我们不好展示，那我们就假设图像就只有2个特征，用2个维度表示图像。那线性分类器的本质就是划分分界线(面)。我们上面的网络输入有3072个神经元，输出有10个神经元，是不是就是我们建立了10个线性变换：从3072维变换到1维。也就是我们建立了10个线性方程组。当我们令方程组的y=0时，就是这个方程组的分界线。我们有10个方程组，所以可以画出10个分界面，我们就是通过这些分界面来分类的。下图的红色箭头就是分界面的法方向，离分界面的法方向越远，这个类别的得分就越高，意思就是这个样本属于这个类别的把握就越大。

线性分类器的决策边界：

Multiclass SVM optimization demo

（3）通过神经网络，进一步反思模板(卷积核)：

第一，模板的意义？
模板记录的是类别的统计信息。模板的作用是通过图片和模板的匹配来进行分类的。

第二，如何设计模板？
既然深度学习网络的权值学习的是图像的模板，那我能不能多建立一些模板，尤其是本例中的马的图片，能不能学两张模板，一张记录马头朝左，一张记录马头朝右。那我的预测精度是不是就会提高很多？所以模板个数是可以人为设置其数量的。

那么，如果我把神经网络设置成两层：f = W2 max(0, W1X + b1) + b2，那如果把w1看作模板，而且这个模板的个数我设置得非常非常多，那w1就是网络学到的图像的非常非常多的特征信息；同理，w2就可以看作是融合w1的多种信息结果，来实现最终类别打分。所以，我们是不是可以通过模板组对图像进行处理操作，就从单一模板飞跃到了模板组！
而且这种模板组的好处还有：比如一些模板学了眼睛、一些模型学了鼻子、而另外的一些模板则学了嘴巴，这是如何一张脸的眼睛被遮挡住了，是不是也不妨碍对这张脸的识别啊。学术一点就是增加了模型的泛化能力。
其实这就是特征提取的过程。如果我特征提取得非常好，那遮挡问题就解决了。比如识别人脸，如果带着太阳镜，虽然双眼被遮住了，但区域特征中还有鼻子和嘴巴等部位，如果我其他局部的特征都符合，就也能判断出来。所以我们要大量的模板，以便提取更多的局部特征。

第三，激活函数是用来解决线性不可分的
线性可分：至少存在一个线性分界面能把两类样本没有错误的分开。
DNN神经网络就相当于级联了多个线性分类器，其中的激活函数就相当于进行了非线性变换。

所以，以后即使架构图中没有标出激活层，我们都是默认有激活函数的。

3、RNN诞生：当卷积操作遇到了深度学习
前面一直说深度学习的灵魂就是通过损失函数，让模型自己找到最佳的参数，那是不是卷积核也可以通过模型自己学习呢？前面我们苦哈哈人为设计的48个卷积核组也不是通适所有图片的，那我能不能设计出类似DNN灵魂的另外一种架构，让模型自己学习卷积核组。其实也不用设计，前面我们的卷积操作不就相当于单层DNN吗，我也类似DNN叠加卷积层即可，而DNN中的激活层就类似我们前面的统计操作——求均值，于是之于DNN激活层的CNN池化层诞生了。于是CNN在架构上的雏形形成了。