使用邻接点偏移量数组解决 BFS 类问题

引言：

        在算法和数据结构中，BFS（广度优先搜索）是一种常用的图搜索算法。它通过逐层遍历图的节点，以找到目标节点或者确定最短路径。然而，在解决 BFS 类问题时，我们经常遇到需要确定节点的邻居，并对它们进行相应处理的情况。这时候，使用邻接点偏移量数组能够提供一种简洁和高效的解决方案。

---

正文：

        1.广度优先搜索算法及其应用场景：

        广度优先搜索算法（BFS）是一种基于队列的遍历算法，常用于流程分析、迷宫游戏等领域。它通过逐层遍历图的节点，以找到目标节点或者确定最短路径，具有广泛的应用前景。

        在 BFS 中，我们从一个初始节点开始，将其加入队列中，然后遍历该节点的所有邻居节点，并把它们也加入队列，直到队列为空。这里所遍历的邻居节点指与当前节点直接相连的节点。遍历过程中，我们需要记录每个节点的状态，以避免重复访问和死循环。同时，我们还需要记录路径信息，以便找到最短路径。

        2.邻接点偏移量数组的概念和作用：

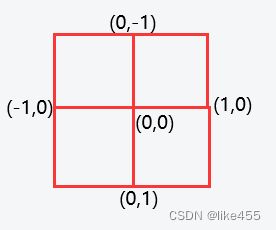
        邻接点偏移量数组是一种用于表示节点邻居关系的数据结构。例如，在一个二维矩阵中，某个节点的坐标为 (x,y)，那么它的上下左右四个邻居节点坐标可以表示为：

                                上：(x-1,y)

        左：(x,y-1)                                右：(x,y+1)

                                下：(x+1,y)

针对上面的四个邻居，我们可以定义一个邻接点偏移量数组 offset，其中 offset[0] = [-1,0] 表示上方邻居的偏移量，offset[1] = [1,0] 表示下方邻居的偏移量，以此类推。那么我们可以通过如下方式计算节点 (x,y) 的邻居坐标：

int[][] offset = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} }; // 邻接点偏移量数组

int x = currentNode.getX(); // 当前节点的x坐标
int y = currentNode.getY(); // 当前节点的y坐标

for (int i = 0; i < 4; i++) {
    int nx = x + offset[i][0]; // 计算邻居节点的x坐标
    int ny = y + offset[i][1]; // 计算邻居节点的y坐标

    // 在这里可以根据邻居节点的坐标进行相应的操作

}

例题：AcWing蛇形矩阵

输入两个整数 n和 m，输出一个 n行 m列的矩阵，将数字 1到 n×m按照回字蛇形填充至矩阵中。

具体矩阵形式可参考样例。

输入格式
输入共一行，包含两个整数 n和 m。

输出格式
输出满足要求的矩阵。

矩阵占 n行，每行包含 m个空格隔开的整数。

数据范围
1≤n,m≤100
输入样例：
3 3
输出样例：
1 2 3
8 9 4
7 6 5

代码：

import java.util.Scanner;

public class Main{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[][] res = new int[n][m];
//        创建偏移量
        int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
//        当前位置
        int x = 0, y = 0, d = 1;

        for (int i = 1; i <= n * m; ++i) {
            res[x][y] = i;
//            a， b为上右下左某一个位置
            int a = x + dx[d], b = y + dy[d];

            if (a < 0 || a >= n || b < 0 || b >= m || res[a][b] > 0) {
                d = (d + 1) % 4;
                a = x + dx[d];
                b = y + dy[d];
            }
            x = a;
            y = b;
        }
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                System.out.print(res[i][j] + " ");
            }
            System.out.println();
        }
    }
}

 运行结果：

        在该题中，定义了偏移量数组 dx 和 dy，用于计算邻居节点的坐标。数组中第 i 个位置的偏移量 (dx[i], dy[i]) 分别表示向左、向下、向右和向上移动一步时的坐标变化。

        然后，你使用循环从 1 到 n×m 遍历每个数字，将当前的数字 i 填入矩阵的当前位置 (x, y) 中，并更新 x 和 y 的值。

        然后，判断是否“撞墙”，你计算下一个位置 (a, b)。如果 (a, b) 超出了矩阵边界或者已经被填充过了，说明需要改变方向。此时，你将方向 d 递增 1 并取模 4，重新计算 (a, b) 的值。

最后，遍历打印矩阵中的每个元素。这样就得到了按回字蛇形填充的矩阵。

---

3.分析算法的时间复杂度和空间复杂度，以及优缺点。

        时间复杂度为 O(n * m)，其中 n 表示矩阵的行数，m 表示矩阵的列数。主要是因为我们需要遍历整个矩阵来填充数字。

        空间复杂度为 O(n * m)，因为我们需要创建一个大小为 n 行 m 列的二维数组来表示最终的矩阵。

优点：

1. 简单直观：该算法使用了模拟的方法，通过逐个遍历填充数字来生成回字蛇形矩阵，易于理解和实现。
2. 时间复杂度低：算法的时间复杂度为线性级别，与矩阵的大小成正比，因此在大部分情况下效率较高。

缺点：

1. 空间占用较大：为了存储矩阵，需要额外创建一个大小为 n 行 m 列的二维数组。当矩阵较大时，会占用较多的内存空间。
2. 不具有通用性：该算法仅适用于回字蛇形填充矩阵的特定问题，对于其他类型的矩阵填充问题并不适用。

例题：在看一道类似AcWing题目  走马日问题 / 移动骑士 

只能以 2*3 的 对角线 移动

给定一个 n∗n 的棋盘，以及一个开始位置和终点位置。

棋盘的横纵坐标范围都是 0∼n−1。

将一个国际象棋中的骑士放置在开始位置上，请问将它移动至终点位置至少需要走多少步。

一个骑士在棋盘上可行的移动方式如下图所示：

输入格式

第一行包含整数 T，表示共有 T 组测试数据。

每组测试数据第一行包含整数 n，表示棋盘大小。

第二行包含两个整数 x,y 用来表示骑士的开始位置坐标 (x,y)。

第三行包含两个整数 x,y 用来表示骑士的终点位置坐标 (x,y)。

输出格式

每组数据输出一个整数，表示骑士所需移动的最少步数，每个结果占一行。

数据范围

4 ≤ n ≤ 300，
0 ≤ x, y ≤ n−1

输入样例：

3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1

输出样例：

5
28
0

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main {
static class Pair{
int x;
int y;

    public Pair(int x, int y) {
        this.x = x;
        this.y = y;
    }
}

static int[] dx = new int[]{-2, -1, 1, 2, 2, 1, -1, -2};
static int[] dy = new int[]{1, 2, 2, 1, -1, -2, -2, -1};

public static void main(String[] args) {
    Scanner sca = new Scanner(System.in);
    int T = sca.nextInt();
    while (T -- > 0) {
        int n = sca.nextInt();
        int sx = sca.nextInt();
        int sy = sca.nextInt();
        int ex = sca.nextInt();
        int ey = sca.nextInt();

        int ans = dfs(n, sx, sy, ex, ey);
        System.out.println(ans);
    }
}

public static int bfs(int n, int sx,int sy, int ex, int ey) {
    int[][] dist = new int[n][n];
    for (int i = 0; i < n; ++ i) {
        Arrays.fill(dist[i], -1);
    }

    Queue queue = new LinkedList<>();
    queue.offer(new Pair(sx,sy));
    dist[sx][sy] = 0;

    while (!queue.isEmpty()) {
        Pair cur = queue.poll();
        int x = cur.x;
        int y = cur.y;
        if (x == ex && y ==ey) {
            return dist[x][y];
        }


        for (int i = 0; i < 8; ++ i) {
            int nx = x + dx[i], ny = y + dy[i];

            if (nx >= 0 && nx < n && ny >= 0 && ny < n && dist[nx][ny] == -1) {
                queue.offer(new Pair(nx,ny));
                dist[nx][ny] = dist[x][y] + 1;
            }
        }
    }
    return -1;

    }
}

        在这里定义Pair类是为了方便存储位置的坐标(x, y)，以及将其作为队列元素存入队列中。使用自定义的Pair类可以更直观地表示位置，并且可以方便地进行存储和传递。

        这种做法是为了增加代码的可读性和可维护性。如果直接使用数组或者其他方式存储位置坐标，可能会导致代码难以理解和维护。通过定义Pair类，可以明确表达每个元素代表一个坐标点，提高代码的可读性。

对于bfs核心函数：

        使用BFS算法搜索最短路径的核心函数。

        首先，创建一个二维数组dist，用于记录每个位置的最短步数。初始化时，将所有位置的步数设置为-1，表示尚未访问过。

        然后，创建一个队列queue，用于存储待搜索的位置。将起点位置(sx, sy)加入队列，并将其步数dist[sx][sy]设置为0，表示起点位置已经访问过，步数为0。

        进入循环，直到队列为空为止。在每次循环中，从队列中取出当前位置(x, y)。检查当前位置是否为终点位置(ex, ey)，如果是，则说明已经找到了最短路径，直接返回dist[x][y]，即当前位置的步数。

        遍历当前位置的所有邻居节点，通过计算当前位置(x, y)和dx、dy数组的组合，可以得到邻居节点的坐标(nx, ny)。

        如果邻居节点(nx, ny)在合法的范围内并且尚未访问过(即dist[nx][ny] == -1)，则将其加入队列，并更新其步数为dist[x][y] + 1，表示从起点到邻居节点的步数。通过这样的操作，不断扩展可行的邻居节点，并更新它们的步数，以便在后续的搜索中能够得到最短路径。

        当队列为空时，说明无法到达终点位置，返回-1，表示不存在最短路径。

总结：

        使用邻接点偏移量数组解决 BFS 类问题能够大幅简化代码，并提高算法的可读性和可维护性。它将节点的邻居确定和处理过程规范化，并且适用于各种需要进行邻居操作的场景。在解决 BFS 类问题时，邻接点偏移量数组是一个有力的工具，值得深入学习和掌握。