《数据结构》第七章:树和森林
在客观世界中,存在着诸多如行政机构、磁盘目录和族谱的组织结构,与动物分类类似,是一种层次化结构,可采用树形结构表示。譬如磁盘目录,一个目录的子目录通常不止两个,无法用二叉树表示,需要采用多叉树的形式,即每个结点可以有不同数目的子结点。
7.1树的定义
树是含有n个结点的有限集合。在任意一棵非空树中:
- 有且仅有一个特定的称为根的结点
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每一个集合本身也是一棵树。并且T1,T2,…,Tm称为根的子树。
树中的相关概念,如结点的度、孩子结点和双亲结点等,定义与二叉树中的相同。
森林是m(m≥0)棵互不相交的树的集合,可记为F=(T1,T2,…,Tm)。对树中的每个结点而言,其子树的结合即为子树森林。
7.2树的存储结构
树的存储结构有多种,可以应用于不同场合。但无论采用哪种存储结构,都要求其不仅能存储各结点本身的信息,还能表示树中各结点之间存在的关系。
7.2.1双亲表示法
在树中,除根结点没有双亲(即父结点)外,其他结点的双亲是唯一确定的。根据这个特性,可用数组存储树中结点及其关系。数组中的每个分量含有两个域:元素值data和该结点的双亲位置parent。树的这种表示方法称为双亲表示法。
树的双亲存储结构类型定义如下:
typedef struct PTNode{
TElemType data;//数据域
int parent;//双亲位置,根结点的parent值为-1
}PTNode;//双亲结点类型
typedef struct{
PTNode *nodes;//由初始化分配的结点数组
int r,nodeNum;//根结点和结点数
}PTree;//树的双亲存储结构类型显然,这种存储结构可由parent直接找到双亲,并可容易地找到所有祖先。但如果需要查找结点的孩子及其子孙,则需要遍历整个结构。
7.2.2双亲孩子表示法
双亲孩子表示法是对双亲表示法的扩展,为各结点构造孩子单链表,以便访问结点的孩子及其子孙。在结点数组元素增加firstChild域作为结点的孩子链表头指针。在孩子链表中,每个结点包含孩子在结点数组的位置child Index和指向下一个孩子结点的指针nextChild。
树的双亲孩子存储结构的类型定义如下:
typedef struct ChildNode{
int ChildIndex;//孩子在结点数组的位置
struct ChildNode *nextChild;//下一个孩子
}ChildNode;//孩子链表中的结点类型
typedef struct{
TElemType data;//元素值
int parent;//双亲位置
struct ChildNode *firstChild;//孩子链表头指针
}PCTreeNode;//双亲孩子结点类型
typedef struct{
PCTreeNode *nodes;//结点数组4
int nodeNum,r;//结点元素个数、根位置
}PCTree;//树的双亲孩子存储结构类型双亲孩子表示法存储了孩子结点的信息,便于实现涉及孩子或双亲的操作。若不涉及双亲操作,则可以去掉parent域,简化为孩子链表存储结构。
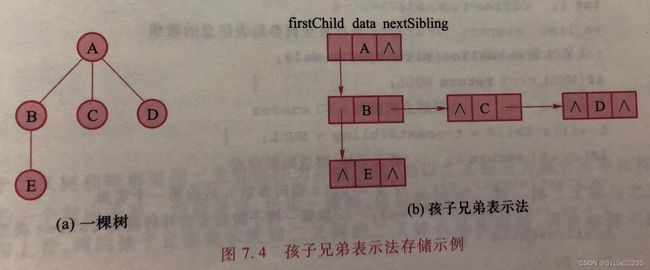
7.2.3孩子兄弟表示法
在树中,结点的最左孩子(第一个孩子)和右兄弟(下一个孩子)如果存在则都是唯一的。因此,孩子兄弟表示法采用二叉链式存储结构,每个结点包含三个域:元素值域data、最左孩子指针firstChild和右兄弟指针nextSibling。
树的孩子兄弟链表的类型定义如下:
typedef struct CSTNode{
TElemType data;//数据域
struct CSTNode*firstChild,*nextSibling;//最左孩子指针、右兄弟指针
}CSTNode,*CSTree,*CSForest;//孩子兄弟链表以下是基于孩子兄弟表示法的树接口。
Status InitTree(CSTree &L);//构造空树L
CSTree MakeTree(CSTree &T);//创建根结点e和n棵子树的树
Status DestroyTree(CSTree &T);//销毁树T
int TreeDepth(CSTree T);//返回树T的深度
CSNode*Search(CSTree T,TElemType e);//查找树T中的结点e并返回其指针
Status InsertChild(CSTree &T,int i,CSTree c);//插入c为T的第i棵子树,c非空并与T不相交
Status DeleteChild(CSTree &T,int i);//删除T的第i棵子树上述基本接口未提供双亲操作,如果需要频繁访问双亲结点,则可在结点中增设parent指针域。下面给出几个基本接口的实现。
1.创建树。
该操作创建一棵有n棵子树的树,根结点值为e。由于子树数目事先无法确定,所以需要使用变长参数,并使用标准库stdarg以获取n棵子树的实参。
算法:创建树
#include //标准头文件,提供宏va_start、va_arg和va_end//用于存储变长参数
CSTree MakeTree(TElemType e,int n,...){
//创建根结点e和n棵子树的树,变长参数为n棵子树
int i;
CSTree t,p,pi;
va_list argptr;//argptr是存放变长参数表信息的数组
t=(CSTree)malloc(sizeof(CSTNode));//开辟空间
if(NULL==t)
{
return NULL;//开辟失败
}
t->data=e;//根结点的值为e
t->firtsChild=t->nextSibling=NULL;
if(n<=0)
{
return t;//若无子树,则返回根结点
}
va_start(argptr,n);//令argptr指向参数n后的第一个实参
p=va_arg(argptr,CSTree);//取第一棵子树的实参转换为CSTree类型
t->firstChild=p;
pi=p;
for(i=1;inextSibling=p;
pi=p;
}
va_end(argptr);//取实参结束
} 2.插入第i棵子树。
插入树c作为树T的第i棵子树。当树非空时,若i==1,则树c直接作为第一颗子树插入;否则,先确定第i-1棵子树的位置,然后将c子树插入其后
算法:插入第i棵子树
Status InsertChild(CSTree &T,int i,CSTree c)
{
//插入c作为T的第i棵子树,c非空并与T不相交
int j;
CSTree p;
if(NULL==T||i<1)
{
return ERROR;//树为空
}
if(i==1)
{
//c插入为T的第1棵子树
c->nextSibling=T->firstChild;
T->firstChild=c;//c成为T的第一棵子树
}
else
{
p=T->firstChild;//p指向T的第i棵子树
for(j=2;p!=NULL&&jnextSibling;//寻找插入位置
}
if(j==i)//找到插入位置
{
c->nextSibling=p->nextSibling;
p->nextSibling=c
}
else
{
return ERROR;//插入位置i过大
}
}
return OK;
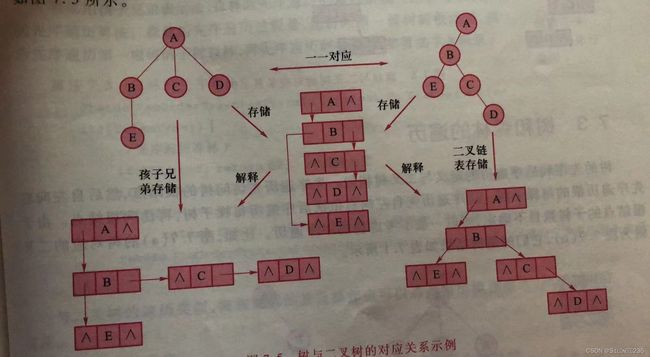
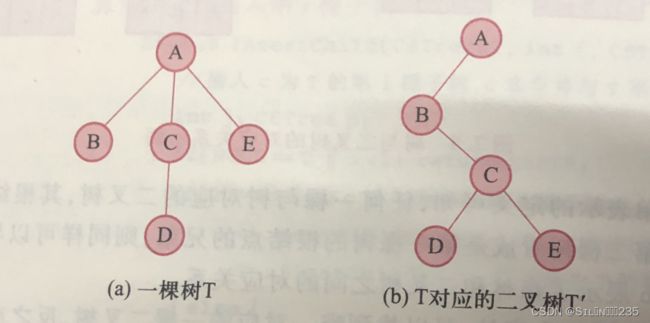
} 由于二叉树和树都可以二叉链表作为存储结构,则以二叉链表为媒介可导出树与二叉树之间的一个对应关系。也就是说,给定一棵树,可以找到唯一的一棵二叉树与之对应,从存储结构上看,树的孩子兄弟表示法和二叉树的二叉链表是相同的,只是解释不同而已。
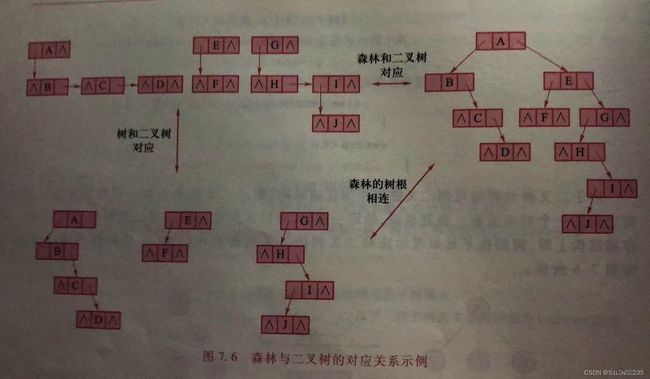
从树的孩子兄弟表示的定义可知,任何一棵树与树对应的二叉树,其根结点的右子树必为空。若把森林中的第二棵树看成第一棵树的根结点的兄弟,则同样可以导出森林和二叉树的对应关系。
因此,给定一棵树或一个森林,可以找到唯一对应的一棵二叉树,反之亦然。这样,对数或森林的操作可以参考二叉树的相应操作实现。
7.3树和森林的遍历
树的先序和后序遍历的定义与二叉树相似。先序遍历先访问树的根结点,然后自左向右先序遍历根的每棵子树;序遍历先自左向右依次后序遍历每棵子树,再访问根结点。由于根结点的子树数目不确定,所以一般不考虑树的中序遍历。
树的先序遍历结果与对应二叉树的先序遍历结果一致,而树的后序遍历结果则与对应二叉树的中序遍历的结果一致。
由于森林与二叉树的一一对应关系,可将森林划分为3个部分:根结点、根结点的子树森林(即对应二叉树的子树)和除去第一棵树之外剩余的树构成的森林(简称剩余森林,即对应二叉树的右子树)。树是特例,是只有一棵树的森林,其余剩余森林为空。
当采用孩子兄弟表示法,森林的先序遍历的递归实现可以参考二叉树的先序遍历算法。森林的先序遍历过程是,先访问第一棵树的根结点,然后先序遍历第一棵树的子树森林,再先序遍历剩余森林。
算法:森林的先序遍历
Status PreOrderTraverseForest(CSForest F,Status(*visit)(TElemType))
{
//先序遍历森林F
if(NULL==F)
{
return OK;//森林为空
}
if(ERROR==visit(F->data))
{
return ERROR;//访问第一棵树的根结点
}
if(ERROR==PreOrderTraverseForest(F->firstChild,visit))
{
return ERROR;//递归先序遍历第一棵子树森林
}
return PreOrderTraverseForest(F->nextSibling,visit);//递归先序遍历剩余森林
}与二叉树的遍历类似,树和森林的其他操作也可以通过遍历操作来实现。
1.求森林的深度
森林的深度应为“第一棵树的子树森林的深度加1”和“剩余森林的深度”之间的较大值
算法:求森林的深度
int ForestDepth(CSForest F){//求森林F的深度
int dep1,dep2,dep;
if(NULL==F)
{
dep=0;//森林为空,深度为0
}
else
{
dep1=ForestDepth(F->firstChild);//求第一棵子树森林的深度
dep2=ForestDepth(F->nextSibling);//求剩余森林的深度
dep=dep1+1>dep2?dep1+1:dep2;//森林的深度
}
return dep;
}2.森林的查找
森林的查找操作Search是在森林F中查找结点e,可采用森林的先序遍历来实现.若查找成功则返回结点的指针,否则返回NULL.
算法:森林的查找
CSTNode *Search(CSForest F,TElemType e)
{
//查找森林F中的结点e并返回其指针
CSTNode *result=NULL;
if(NULL==F)
{
return NULL;//森林为空,返回NULL
}
if(F->data==e)
{
return F;//找到结点,返回其指针
}
if((result=Search(F->firstChild,e))!=NULL)//在第一棵树的子树森林查找
{
return result;
}
return Search(F->nextSibling,e);//在剩余森林中查找
}7.4并查集
在集合的一些应用中,需将n(n>0)个不同的元素划分为若干个等价的子集。这类问题的一种解决办法是,首先令每个元素自成一个单元素集合,然后将等价的元素所属的集合合并。
并查集合适描述这类问题。
例如,一致三个人A,B,C,他们之间可能存在亲戚关系,比如A和B是亲戚,B和C也是亲戚关系,能否从这些信息中判断A和C是否为亲戚?解决办法是首先令每个人自成一个集合{A},{B},{C},根据存在的两两亲戚关系,将两个人所属的集合合并,最终可得到一个集合{A,B,C},从而得到A和C是亲戚关系。
并查集是指一组不相交的子集所构成的集合,记作
S={S1,S2,S3,…,S4}
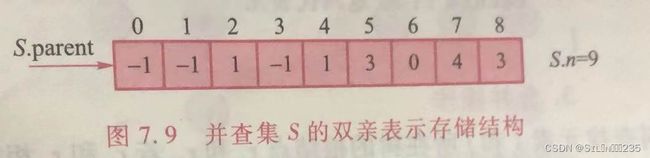
其中,任意两个子集Si和Sj(1≤i≠j≤n)两两不相交。每个子集选取某个元素作为其标识,称为代表元。约定在存储含m个数据元素的并查集前,需对所有元素进行0
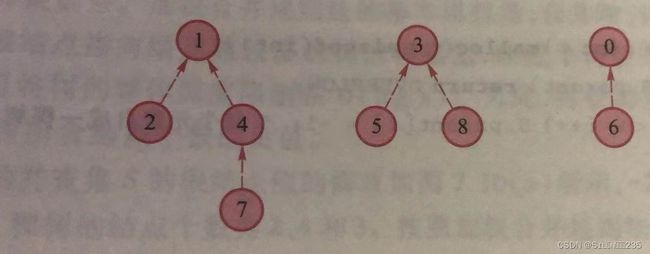
到m-1的编号,并用编号表示对应的元素。例如,有9个数据元素,依次编号为0至8,根据等价关系构成并查集S={S1,S2,S3},其中S1={1,2,4,7},S2={3,5,8},S3={0,6},子集S1,S2,S3两两不相交。
并查集通常需要以下两种操作:
- 查找某个元素所属的子集,简称查找(Find)操作。
- 合并两个元素所属的集合,简称合并(Union)操作。
为了高效地实现上述操作,可用森林F=(T1,T2,T3,…,Tn)来表示并查集S。森林中地每棵树Ti(1≤i≤n)表示并查集S中的一个子集Si,Ti中每个结点表示Si中的一个元素,根结点作为代表元。为方便操作,结点应含有指向双亲结点的位标
其中S1={1,2,4,7},S2={3,5,8},S3={0,6}
上述森林易于实现并查集的操作。并查集可采用森林的双亲表示法作为存储结构,其类型定义如下:
typedef struct{
int *parent;//双亲数组,其数组下标表示元素,数组存储对应元素所属树
//的双亲结点的位序,当为-1时,表示是树的根结点
int n;//森林的结点数目
}PForest,MFSet;//森林、并查集并查集的基本操作可定义为如下接口:
Status InitMFSet(MFSet &S,int n);//构造由n个单元子集构成的并查集S
Status DestroyMFSet(MFSet &S);//销毁并查集S
int FindMFSet(MFSet &S,int i);//查找元素i并在并查集S中的所属的子集,返回其代表元
Status DiffMFSet(MFSet &S,int i,int j);//判断并查集S中的元素i和j是否在同一子集;若是,返回TRUE,否则返回FALSE
Status UnionMFSet(MFSet &S,int i,int j);//合并并查集S中元素i和j所属的两个子集。1.并查集的初始化
该操作分配指定容量n的存储空间,且存储空间的初值置为-1,即每个元素自成一棵树。
算法:并查集的初始化
Status InitMFSet(MFSet &S,int n)//构造由n个单元素子集构成的并查集S
{
int i;
S.parent=(int *)malloc(n*sizeof(int));//开辟空间
if(NULL==S.parent)
{
return OVERFLOW;//开辟失败
}
for(int i=0;i2.查找操作
该操作是从元素i(即下标i)出发,沿着双亲数组的值一直找到根结点(根结点的值小于0),并返回根结点的位置。
算法:并查集的查找
int FindMFSet(MFSet &S,int i)//查找i在并查集S中所属子集,返回代表元
{
if(i<0||i>S=S.n)
{
return -1;//元素i不存在
}
while(S.parent[i]>0)
{
i=S.parent[i];//沿双亲位标链找到根结点
}
return i;//返回代表元
}3.合并操作
该操作首先分别查找元素i和j所在树的根结点ri和rj,若ri和rj相等,则是同一子集,无需合并;否则吧根结点ri(或rj)的双亲结点值置为rj(或ri)。
算法:并查集的子集合并
Status Union(MFSet &S,int i,int j)
{
//合并并查集S中元素i和j所属的两个子集
int ri,rj;
if(i<0||i>=S.n||j<0||j>=S.n)
{
return FALSE;//元素i和j找不到
}
ri=FindMFSet(S,i);//i的根结点
rj=FindMFSet(S,j);//j的根结点
if(ri==rj)
{
return FALSE;//ij本就为一个子集,无需合并
}
S.parent[ri]=rj;//把根结点ri的双亲结点置为rj,实现合并
return TRUE;
}合并操作所需的时间主要取决于查找长度,即树的高度。有两种改进方法可降低树的高度:加权合并规则法和路径压缩法
1.加权合并规则法
加权合并规则法的基本思路是,合并时,让结点数较少的跟根结点指向结点数较多的树的根结点,即把小树合并到大树里面。此方法可将树的整体深度限制在O(log n)。为此,将根结点存储的“-1”该为该树所含结点个数的负值。
算法:采用加权合并规则的合并
Status UnionMFSet(MFSet &S,int i,int j){
//采用加权合并规则法合并并查集S中元素i和j所属的两个子集
int ri,rj;
if(i<0||i>=S.n||j<0||j>=S.n)
{
return FALSE;//查找不到
}
ri=FindMFSet(S,i);
rj=FindMFSet(S,j);
if(ri==rj)
{
return FALSE;
}
if(S.parent[ri]>S.parent[rj])
{
//注意:比较的是结点个数的负值
S.parent[rj]+=S.parent[ri];//两个均为负值
S.parent[ri]=rj;//将元素i的子集并到元素j所在的子集
}
else
{
S.parent[ri]+=S.parent[rj];//两个均为负值
S.parent[rj]=ri;//将元素j的子集并到元素i所在的子集
}
return TRUE;
}2.路径压缩法
路径压缩法更为高效,在查找结点所在树的根结点的过程中,置查找路径上的每个结点的双亲位标值为根结点。
算法:采用路径压缩法的查找
int FindMFSet_PC(MFSet &S,int i)
{
//采用路径压缩法查找元素i在并查集S中所属的子集,返回该子集的代表元
if(i<0||i>=S.n)
{
return -1;//查找不到
}
if(S.parent[i]<0)
{
return i;//找到根结点
}
S.parent[i]=FindMFSet_PC(S,S.parent[i]);//i的双亲值置为根结点
return S.parent[i];//返回根结点
}并查集可应用于许多实际问题中。如判断是否为亲戚的问题,初始时每个人自成一个子集;若a和b存在亲戚关系,则合格两个人所在的子集;如此重复,直至处理完所有已知的亲戚关系。于是亲戚关系判定转化为判断任意两个人是否为同一子集。
算法:判断亲戚
Status hasRelationship(MFSet &S,int a,int b)
{
//判断元素a和b是否是亲戚,若是则返回TRUE,否则返回FALSE
if(a<0||b<0||a>=S.n||b>=S.n)
{
return FALSE;//查找失败
}
if(FindMFSet_PC(S,a)==FindMFSet_PC(S,b))
{
return TRUE;
}
else
{
return FALSE;
}
}7.5 B树
二叉查找树树和二叉平衡树都是典型的二叉查找树的结构,其查找的时间复杂度与树的高度相关。一般而言,树的高度越低,则查找效率越高。为了降低树的高度,可令每个结点存储更多元素,将平衡二叉树扩展为平衡多叉查找树。
7.5.1 B树的定义
一棵m阶B树,或为空树,或为满足以下特性的m叉树:
- 树中的每个结点最多含有m棵子树。
- 若根结点是非终端结点,则至少有两颗子树。
- 除根结点之外的所有非终端结点至少有⌈m/2⌉棵子树。
- 每个非终端结点中包含信息:(n,A0,K1,A1,K1,A2,…,Kn,An)。其中:
- Ki(1≤i≤n)为关键字,且关键字按升序排序。
- 指针Ai(0≤i≤n)指向子树的根结点,Ai-1指向子树中所有结点的关键字均小于Ki,且大于Ki-1.
- 关键字的个数n必须满足:⌈m/2⌉-1≤n≤m-1.
- 所有子叶结点必须出现在同一层,叶子结点不包含任何信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空。
实际上,B树的结点还应包含n个指向每个关键字相应记录的指针。
B树主要用于文件的检索,查找操作涉及外村的读取。m阶B树的结点类型定义如下:
#define m 3//B树的阶数,此处设为3
typedef struct{
int keynum;//结点当前的关键字个数
KeyType key[m+1];//关键字数组,key[0]未用
struct BTNode *parent;//双亲结点指针
struct BTNode *ptr[m+1];//孩子结点的指针数组
Record *recptr[m+1];//B树的结点及指针类型
}BTNode,*BTree;//B树的结点及指针类型7.5.2 B树的查找
B树的查找从根结点开始,重复以下过程:若给定关键字等于结点中的某个关键字Ki,则查找成功;若给定关键字比结点中的Ki小,则进入指针A0指向下一层结点继续查找;若在两个关键字Ki-1和Ki之间,则进入它们之间的指针Ai—1指向的下一层结点继续查找;若比该结点所有关键字大,则在其最后一个指针An指向的下一层结点继续查找;若找到叶子结点,则说明给定值对应的数据记录不存在,查找失败。
由于查找需要返回的信息包括找到的结点、该结点中关键字位序以及查找标记,所以将这些信息封装成一个结构体。
算法:B树的查找
typedef struct{
BTree pt;//指向找到的结点
int i;//1≤i≤m,在结点中的关键字位序
int tag;//1:查找成功;0:查找失败
}result;//B树查找结构类型
void SearchBTree(BTree t,int k,result &r)
{
//在m阶B树t上查找关键字k,用r返回(pi,i,tag)
//若查找成功,则标记tag=1,指针pt所指结点中第i个关键字等于k
//否则tag=0,若要插入关键字为k的记录,应位于pt结点中第i-1个和第i个关键字之间
int i=0,found=0;
BTree p=t,q=NULL;//初始,p指向根结点;p将用于指向待查结点,q指向其双亲
while(p!=NULL&&0==found)
{
i=Search(p,k);//在p->key[1..p->keynum]之间查找p->key[i-1]key[i]
if(i<=p->keynum&&p->key[i]==k)
{
found=1;//找到待查关键词
}
else
{
q=p;
p=p->ptr[i-1];//指针下移
}
}
if(1==found)//查找成功,返回k的位置和p及i
{
r.pt=p;
r.i=i;
r.tag=1;
}
else//查找不成功,返回k的插入位置q及i
{
r.pt=q;
r=i;
r.tag=0;
}
}
int Search(BTree p,int k)
{
//在p->key[1..p->keynum]找k
int i=1;
while(i<=p->keynum&&k>p->key[i])
{
i++;
}
return i;
} 7.5.3 B树的插入
B的插入过程可描述为,利用B树的查找操作查找关键字k的插入位置。若找到,则说明该关键字已经存在,直接返回;否则查找操作失败于某个最底层的非终端结点上,在该结点插入后,若其关键字总数n未达到m,算法结束,否则需分裂结点。
分裂的方法是,生成一新结点,从中间位置把结点(不包括中间位置的关键字)分成两部分。前半部分留在旧结点中,后半部分复制到新结点中,中间位置的关键字连同新结点的存储位置插入到父结点中。如果插入后父结点的关键字个数也超过m-1,则继续分裂。这个向上分裂的过程如果持续到根结点,则会产生新的根结点。
算法:B树的插入操作
void InsertBTree(BTree &t,int k)
{
//在B树t中q结点的key[i-1]和key[i]之间插入关键字k
//若插入后结点关键字个数等于B树的阶,则沿双亲指针链进行结点分裂,使t仍是m阶B树
int x,s,finished=0,needNewRoot=0;
BTree ap;
if(NULL==q)
{
newRoot(t,NULL,k,NULL);//生成新的结点
}
else
{
x=k;
ap=NULL;
while(0==needNewRoot&&0==finished)
{
Insert(q,i,x,ap);//x和ap到q->key[i-1]和q->ptr[i]
if(q->keynumkey[s];
if(q->parent!=NULL)
{
q=q->parent;
i=Search(q,x);//在双亲结点中查找x的插入位置
}
else
{
needNewRoot=1;
}
}
}//while
if(needNewRoot==1)//t是空树或者根结点已分裂为q和ap结点
{
newRoot(t,q,x,ap);//生成含有(q,x,ap)的新的根结点t
}
}
}
void split(BSTree &q,int s,BTree &ap)
{
//将q结点分裂为两个结点,前一半保留在原结点,后一半移入ap所指新结点
int i,j,n=q->keynum;
ap=(BTNode*)malloc(sizeof(BTNode));//生成新结点
ap->ptr[0]=q->ptr[s];
for(i=s+1,j=1;j<=n;i++,j++)//后一半移入ap结点
{
ap->key[j]=q->key[i];
ap->ptr[j]=q->ptr[i];
}
ap->keynum=n-s;
ap->parent=q->parent;
for(i=0;iptr[i]!=NULL)
{
qp->ptr[i]->parent=ap;//
}
q->keynum=s-1;//q结点的前一半保留,修改keynum
}
}
void newRoot(BTree &t,BTree p,int x,BTree ap)
{
//生成新的根结点
t=(BTNode*)malloc(sizeof(BTNode));
t->keynum=1;
t->ptr[0]=p;
t->ptr[1]=ap;
t->key[1]=x;
if(p!=NULL)
{
p->parent=t;
}
if(ap!=NULL)
{
ap->parent=t;
}
t->parent=NULL;//新根的双亲是空指针
}
void Insert(BTree &q,int i,int x,BTree ap)
{
//关键字x和新结点ap分别插入到q->key[i]和q->ptr[i]
int j,n=q->keynum;
for(j=n;j>=i;j--)
{
q->key[j+1]=q->key[j];
q->ptr[j+1]=q->ptr[j];
}
q->key[i]=x;
q->ptr[i]=ap;
if(ap!=NULL)
{
ap->parent=q;
}
q->keynum++;
} 7.5.4 B树的删除
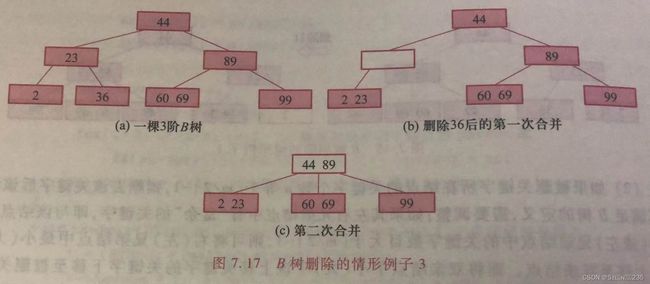
在B树上删除关键字k的过程可利用前述的查找过程找出该关键字所在的结点,然后根据k所在结点是否为最下层非终端结点进行不同的处理。
1.该结点为最下层非终端结点
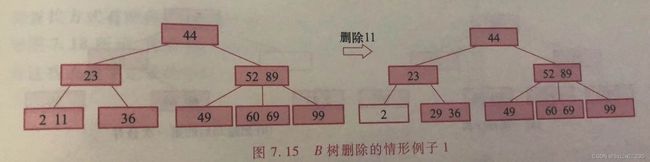
首先直接从该结点删除关键字k,然后根据以下3种可能分别作相应处理。
- 如果被删除关键字结点的原关键字个数n≥⌈m/2⌉,则删去该关键字后该关键字仍满足B树的定义。
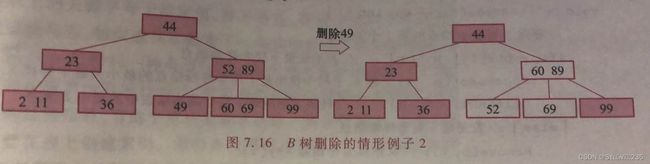
1.如果被删关键字所在结点的关键字个数n等于⌈m/2⌉-1,则删去该关键字后该结点将不满足B树的定义,需要调整:如果其左右兄弟结点中有“富余”的关键字,即与该结点相邻的右(或左)兄弟结点中的关键字数目大于⌈m/2⌉-1,则可将右(左)兄弟结点中最小(大)关键字上移至双亲结点。而将双亲结点中小(大)于该上移关键字的关键字下移至被删关键字所在结点中。
2.如果相邻兄弟结点中没有“多余”的关键字,即相邻兄弟结点中关键字数目均等于⌈m/2⌉-1。此时比较复杂,需把要删除关键字的结点与其左(或右)兄弟结点以及双亲结点中分割两者的关键字Ki一起,合并到Ai-1(或Ai)结点,即删除该关键字结点的左(右)兄弟结点。如果导致双亲结点中关键字个数小于⌈m/2⌉-1,则对此双亲结点做相同的处理。如果直到对根结点也做合并处理,则整棵树减少一层。
2.该结点不是最下层非终端结点
假设被删关键字为该结点中第i个关键字Ki,则可从指针Ai所指的子树中找到位于最下层非终端结点的最小关键字代替Ki,并将其删除。
算法:B树的删除操作
void DeleteBTree(BTree &p,int i)
{
//删除B树上p结点的第i个关键字
if(p->ptr[i]!=NULL)//若不是最下层非终端结点
{
Successor(p.i);//在Ai子树中找到最下层非终端结点的最小关键字代替Ki
DeleteBTree(p,1);//转换为删除最下层非终端结点的最小关键字
}
else//若是最下层非终端结点
{
Remove(p,i);//从结点p中删除key[i]
if(p->keynum<(m-1)/2)//删除后关键字个数小于(m-1)/2、
{
Restore(p,i);//调整B树
}
}
}
void Successor(BTree &p, int i) {
// 在p结点的第i个指针指向的子树中找到最小的关键字代替Ki
// 如果是叶子节点,直接返回
if (p->ptr[i]->leaf) {
return;
}
// 找到最小的关键字,即最左边的子树
BTree successor = p->ptr[i];
while (!successor->leaf) {
successor = successor->ptr[0];
}
// 将最小关键字代替Ki
p->key[i] = successor->key[0];
}
void Remove(BTree &p, int i) {
// 从结点p中删除key[i]
// 将key[i+1:]往前移动
for (int j = i + 1; j <= p->keynum; j++) {
p->key[j-1] = p->key[j];
}
// 将ptr[i+1:]往前移动
for (int j = i + 1; j <= p->keynum + 1; j++) {
p->ptr[j-1] = p->ptr[j];
}
// 关键字数量减一
p->keynum--;
}
void Restore(BTree &p, int i) {
// 调整B树结点p
// 如果左兄弟结点存在且关键字数量大于(m-1)/2,则从左兄弟结点借一个关键字
if (i > 1 && p->ptr[i-1]->keynum > (m-1)/2) {
// 将p的第一个关键字后移一位
for (int j = p->keynum; j >= 1; j--) {
p->key[j] = p->key[j-1];
}
// 将左兄弟结点的最后一个关键字插入到p的第一个位置
p->key[0] = p->ptr[i-1]->key[p->ptr[i-1]->keynum-1];
// 如果左兄弟结点不是叶子节点,将最后一个指针也转移到p
if (!p->ptr[i-1]->leaf) {
p->ptr[0] = p->ptr[i-1]->ptr[p->ptr[i-1]->keynum];
}
// 更新左兄弟结点的关键字数量
p->ptr[i-1]->keynum--;
// 更新p的关键字数量
p->keynum++;
return;
}
// 如果右兄弟结点存在且关键字数量大于(m-1)/2,则从右兄弟结点借一个关键字
if (i <= p->keynum && p->ptr[i+1]->keynum > (m-1)/2) {
// 将p的第i个关键字后移一位
for (int j = p->keynum; j >= i+1; j--) {
p->key[j] = p->key[j-1];
}
// 将右兄弟结点的第一个关键字插入到p的第i个位置
p->key[i] = p->ptr[i+1]->key[0];
// 如果右兄弟结点不是叶子节点,将第一个指针也转移到p
if (!p->ptr[i+1]->leaf) {
p->ptr[i] = p->ptr[i+1]->ptr[0];
}
// 将右兄弟结点的关键字和指针往前移动
for (int j = 1; j <= p->ptr[i+1]->keynum - 1; j++) {
p->ptr[i+1]->key[j-1] = p->ptr[i+1]->key[j];
}
for (int j = 1; j <= p->ptr[i+1]->keynum; j++) {
p->ptr[i+1]->ptr[j-1] = p->ptr[i+1]->ptr[j];
}
// 更新右兄弟结点的关键字数量
p->ptr[i+1]->keynum--;
// 更新p的关键字数量
p->keynum++;
return;
}
// 如果左右兄弟结点的关键字数量都是(m-1)/2,则将关键字从父结点借一个,并和左右兄弟结点合并
if (i > 1) {
// 从父结点借一个关键字
BorrowFromLeftSibling(p, i);
} else {
// 从父结点借一个关键字
BorrowFromRightSibling(p, i);
}
}
void BorrowFromLeftSibling(BTree &p, int i) {
// 从左兄弟结点借一个关键字
// 取得左兄弟结点
BTree leftSibling = p->ptr[i-1];
// 将p的第一个关键字后移一位
for (int j = p->keynum; j >= 1; j--) {
p->key[j] = p->key[j-1];
}
// 将左兄弟结点的最后一个关键字插入到p的第一个位置
p->key[0] = leftSibling->key[leftSibling->keynum-1];
// 如果左兄弟结点不是叶子节点,将最后一个指针也转移到p
if (!leftSibling->leaf) {
p->ptr[0] = leftSibling->ptr[leftSibling->keynum];
}
// 更新左兄弟结点的关键字数量
leftSibling->keynum--;
// 更新p的关键字数量
p->keynum++;
}
void BorrowFromRightSibling(BTree &p, int i) {
// 从右兄弟结点借一个关键字
// 取得右兄弟结点
BTree rightSibling = p->ptr[i+1];
// 将p的第i个关键字后移一位
for (int j = p->keynum; j >= i+1; j--) {
p->key[j] = p->key[j-1];
}
// 将右兄弟结点的第一个关键字插入到p的第i个位置
p->key[i] = rightSibling->key[0];
// 如果右兄弟结点不是叶子节点,将第一个指针也转移到p
if (!rightSibling->leaf) {
p->ptr[i] = rightSibling->ptr[0];
}
// 将右兄弟结点的关键字和指针往前移动
for (int j = 1; j <= rightSibling->keynum - 1; j++) {
rightSibling->key[j-1] = rightSibling->key[j];
}
for (int j = 1; j <= rightSibling->keynum; j++) {
rightSibling->ptr[j-1] = rightSibling->ptr[j];
}
// 更新右兄弟结点的关键字数量
rightSibling->keynum--;
// 更新p的关键字数量
p->keynum++;
}7.5.5 B+树
B+树是应文件系统所需而提出的一种B树的变型。一棵m阶的B+树和m阶B树的差异在于:
- 有n棵子树的结点包含n个关键字。
- 所有子树结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子本身依关键字大小自小而大顺序链接。
- 所有的非终端结点可以看作索引部分,结点中仅含其子树(根结点)中的最大(或最小)关键字。
通常B+树有两个头指针,一个指向根结点,一个指向关键字最小的叶子结点。因此B+树的查找方式有两种:一种是从最小关键字起顺序查找,另一种是从根结点开始,进行随机查找。
在B+树上进行随机查找、插入和删除过程基本上与B树类似。只是在查找时,若非终端结点上的关键字等于给定值,并不终止,而是继续向下直到叶子结点。因此,在B+树,不管查找成功与否,每次查找都是走了一条从根到叶子结点的路径。
索引是B+树的一种典型应用。索引是对数据库中一个或多个列的值进行排序的结构,与在表中搜素所有的行相比,索引用指针指向存储在表中指定列的数据值,然后根据指定的次序排列这些指针,有助于更快地获取信息,通常情况下,只有当经常查询索引列中的数据时,才需要在表上创建索引。索引会占用磁盘空间,并影响数据更新的速度。但是在多数情况下,索引所带来的数据检索速度优势大大超过它的不足之处。