文章目录
-
- A. Square(简单模拟）
- B. Arranging Cats（简单思维）
- C. Sending Messages（贪心）
- D. Very Different Array（贪心）
- E. Eat the Chip（贪心）
- F. Sum of Progression（根号分治）
- G. Mischievous Shooter（前缀和+思维）
A. Square(简单模拟）
思路 ：简单的模拟，将 a i a_{i} ai的总和与 b i b_{i} bi的总和加起来后进行比较即可。
代码如下：
#include
#include
#include
#include
#include
#include
B. Arranging Cats（简单思维）
题意：给定两个01序列a,b,求用以下操作将序列a修改成序列b所需最少的操作数。
操作1：将序列a的某一位0变成1。
操作2：将序列a的某一位1变成0。
操作3：将序列a中的任意一对 ( 0 , 1 ) (0,1) (0,1)进行交换
思路：首先求出序列a和b中的1的总数cnta,cntb，再减去序列a与b中的同时为1的位置的个数，答案就是 m a x ( c n t a , c n t b ) max(cnta,cntb) max(cnta,cntb)
代码如下：
#include
#include
#include
#include
#include
#include
C. Sending Messages（贪心）
题意：给定一个序列arr表示时间，一个人需要在这些时间发送短信，初始时这个人的手机电量为f，每过一个单位的时间，手机的电量会减少a，这个人也可以选择关机，关机后每过一个单位的时间，手机的电量不会改变，但是再次开机时会损耗b的电量。问这个人以最优操作来操作手机，是否能发完所有的短信
思路：我们可以枚举序列arr每两个时间直接扣电和关机时损耗的电量，每次操作都选择最小的操作进行操作，看最后电量是否＞0即可。
#include
#include
#include
#include
#include
#include
D. Very Different Array（贪心）
题意：给定一个长度为n的序列a，再给定一个长度为m的序列b ( m ≥ n ) (m \ge n) (m≥n)，要求在序列b中挑选n个数，组成序列c，使得 ∑ i = 1 n ∣ a i − c i ∣ \sum_{i=1}^{n}|a_i-c_i| ∑i=1n∣ai−ci∣最大
思路：首先将序列a和序列b从小到大排序，我们贪心的选择，序列a的两端i，j，开始向中间，一个一个的来选取对应的 c i c_i ci，那么对于 a i a_i ai和 a j a_j aj如何选取能使得答案最大呢：
定义序列b的两端为 L , R L,R L,R。
那么对于 a i a_i ai有两种选择选择 b L b_L bL和 b R b_R bR。
同样的对于 b j b_j bj也有两种选择 b L b_L bL和 b R b_R bR。
对于这四种情况，我们每次选择最大的情况即可
双指针从两端向中间遍历
代码如下：
#include
#include
#include
#include
#include
#include
E. Eat the Chip（贪心）
题意： 在一个 n ∗ m n*m n∗m 的网格中，放入一个黑色棋子与白色棋子，每一次，白色棋子可以选择向正下方，左下，右下，三个方向移动棋子，黑色棋子每次可以选择正上方，左上，右上三个方向移动棋子。两个棋子都以最优方案操作，如果白色棋子能抓大棋子那么Alice获胜，否则Bob获胜。如果白色棋子走到最底下，黑丝棋子走到最上方，那么就是平局，输出Draw
思路：每一次白色棋子会向下走一步，黑色棋子会向上走一步，因此，我们只需要判断两棋子相遇前的最后一步是谁走的，然后再判断每个棋子应该往哪个方向一直走，例如，最后一步是白色棋子走，那么白色棋子就是白色棋子往黑色棋子的方向走，如果最后一步是黑色棋子走，那么就是黑色棋子向白色棋子的方向走，另一个棋子与之相同的方向走。最后再判断以下二者的位置即可
代码如下：
#include
#include
#include
#include
#include
#include
F. Sum of Progression（根号分治）
题意：给一个长度为n的序列a，有q个询问，对于每个询问q，给定三个参数 s , d , k s,d,k s,d,k来求 a s + a s + d ∗ 2 + … … a s + ( k − 1 ) ∗ d ∗ k a_s+a_{s+d}*2+……a_{s+(k-1)*d}*k as+as+d∗2+……as+(k−1)∗d∗k的总和
思路：这题如果暴力求解很简单，但是一定是会超时的。有一种算法专门处理这类问题，那就是根号分治，根号分治的的思想就是取一个值X，用X把问题分成两个部分，当操作次数 ≤ X \le X ≤X时，可以暴力计算，当操作次数 ≥ X \ge X ≥X时，可以采用之前预处理好的东西直接得到答案。
那么这个 X 取什么值合适呢？对于上述的第一种操作，时间复杂度是 O ( x ) O(x) O(x),对于第二种操时间复杂度为 O ( n x O(\frac{n}{x} O(xn)，那么一次操作的时间复杂度最坏就是 m a x ( O ( x ) , O ( n x ) ) max(O(x),O(\frac{n}{x})) max(O(x),O(xn)),毫无疑问，选择 X = n X=\sqrt{n} X=n 时，时间复杂度是最低的。
现在看一道例题，来更好的了解根号分治这个算法: 洛谷P3396 哈希冲突
这题我们可以把模数看成上述的X，用 m o d [ x ] [ y ] mod[x][y] mod[x][y]表示modx为y的数的总和，预处理出来模数 X ≤ n X\le \sqrt{n} X≤n 时所有的情况，对于 X ≥ n X\ge \sqrt{n} X≥n 的情况， 暴力计算即可，修改也是同样
那么总的时间复杂度就是 O ( N l o g N ) O(NlogN) O(NlogN)
代码在https://www.luogu.com.cn/record/143536024
现在接着看这道题：我们同样可以用根号分治的方案，首先预处理出来所有 d ≤ s q r t ( n ) d \le sqrt(n) d≤sqrt(n)的不带权的前缀和，用 p r e pre pre数组记录下来，也就是首先不管上述题目中的K，然后再计算一个带权的前缀和，用 s p r e spre spre记录。最后我们对于每个s，判断一个是否是 s p r e spre spre数组中的第一项，如果不是，所有的权值都要减小 ( s − 1 ) / d ∗ k (s-1)/d*k (s−1)/d∗k,具体先代
#include
#include
#include
#include
#include
#include
G. Mischievous Shooter（前缀和+思维）
题意：在一个 n ∗ m n*m n∗m的网格中有许多个得分点，给定参数k，可以向一个点的四个方向投放炸弹，会得到该方向长度为 ( k + 1 ) (k+1) (k+1)的三角形内的所有的得分点的总和，问能得到的得分点的总和最大为多少。
思路：这题看似复杂，有四个方向，其实我们只需要选取一个方向，然后旋转网格四次即可，那么我们如果我们选择这个方向的三角形，如何通过递推从 ( i , j − 1 ) (i,j-1) (i,j−1)得到 ( i , j ) (i,j) (i,j)下一个三角形的值呢，只需要加上红色区域的值减去绿色区域的值即可
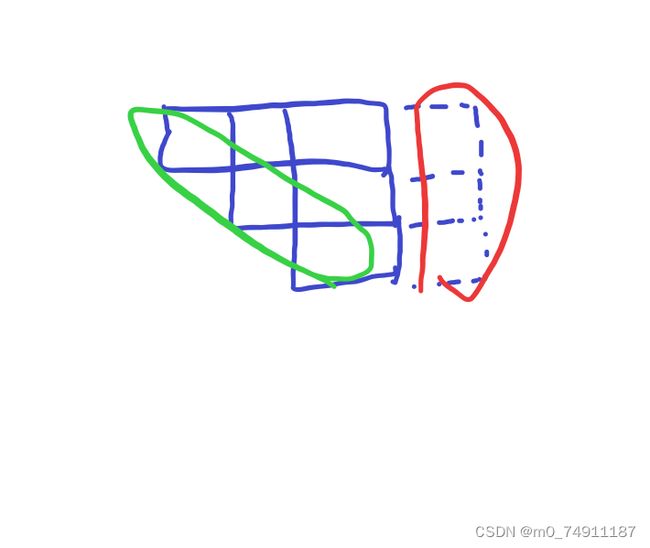因此只要预处理出来列方向上的前缀和和一个对角线方向上的一个前缀和即可。注意要判断一个边界问题。
#include
#include
#include
#include
#include
#include
