算法学习系列（二十四）：二分图

引言

这个二分图作为平常我是不怎么知道的，但是在算法竞赛中还是能用得到的。本文主要介绍了染色法：用来判断如否为二分图，匈牙利算法：求出二分图最大匹配数。

一、二分图

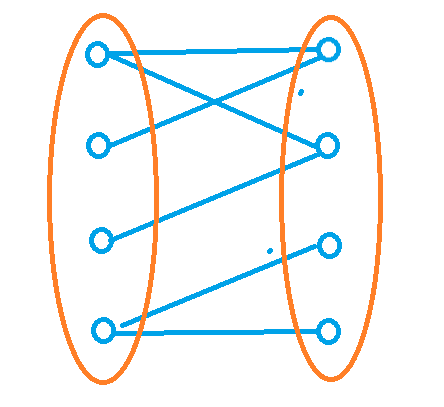
二分图：在两个集合中，集合之间没有边。如下图所示，两个橙色代表两个集合，集合间的点没有边，不同集合间的点才可能有边

二、染色法

用处：用来判断是否为二分图
思想：遍历所有的点，如果没染过，那就把该集合的点全染了，如果染的过程中发现冲突，那就将flag置为false
可以通过一个点就将该集合中的所有点全染了，如下图所示。

题目描述：

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环。

请你判断这个图是否是二分图。

输入格式
第一行包含两个整数 n 和 m。
接下来 m 行，每行包含两个整数 u 和 v，表示点 u 和点 v 之间存在一条边。

输出格式
如果给定图是二分图，则输出 Yes，否则输出 No。

数据范围
1≤n,m≤105

输入样例：
4 4
1 3
1 4
2 3
2 4
输出样例：
Yes

示例代码：

#include 
#include 
#include 

using namespace std;

const int N = 1e5+10, M = N * 2;  //因为是无向图

int n, m;
int h[N], e[M], ne[M], idx;
int color[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool dfs(int u, int c)
{
    color[u] = c;
    
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!color[j])  //没有染
        {
            if(!dfs(j, 3 - c)) return false;
        }
        else if(color[j] == c) return false;  //染了但是染的是相同的颜色
    }
    
    return true;
}

int main()
{
    memset(h, -1, sizeof h);
    
    scanf("%d%d", &n, &m);
    
    while(m--)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }
    
    bool flag = true;
    for(int i = 1; i <= n; ++i)
    {
        if(color[i]) continue;
        if(!dfs(i, 1)) 
        {
            flag = false;
            break;
        }
    }
    
    if(flag) puts("Yes");
    else puts("No");
    
    return 0;
}

三、匈牙利算法

用处：判断一个二分图中成功匹配的最大数。成功匹配：没有两条边共用一个点
思想：有两个图左、右，如果左一匹配了，右一，然后左二只能匹配右一，那就让左一换一个匹配，再让左二匹配右一，如果换不了就不换了，然后就这样一次遍历所有的点

题目描述：

给定一个二分图，其中左半部包含 n1 个点（编号 1∼n1），右半部包含 n2 个点（编号 1∼n2），二分图共包含 m 条边。

数据保证任意一条边的两个端点都不可能在同一部分中。

请你求出二分图的最大匹配数。

二分图的匹配：给定一个二分图 G，在 G 的一个子图 M 中，M 的边集 {E} 中的任意两条边都不依附于同一个顶点，则称 M 是一个匹配。

二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。

输入格式
第一行包含三个整数 n1、 n2 和 m。
接下来 m 行，每行包含两个整数 u 和 v，表示左半部点集中的点 u 和右半部点集中的点 v 之间存在一条边。

输出格式
输出一个整数，表示二分图的最大匹配数。

数据范围
1≤n1,n2≤500,1≤u≤n1,1≤v≤n2,1≤m≤105

输入样例：
2 2 4
1 1
1 2
2 1
2 2
输出样例：
2

示例代码：

#include 
#include 
#include 

using namespace std;

const int N = 510, M = 1e5+10;

int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];  //代表n2所匹配的是谁
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool find(int u)
{
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(st[j]) continue;
        
        st[j] = true;
        if(match[j] == 0 || find(match[j]))  //如果没有匹配或者匹配的找到另一个了
        {
            match[j] = u;  // 匹配
            return true;
        }
    }
    
    return false;
}

int main()
{
    memset(h, -1, sizeof h);
    
    scanf("%d%d%d", &n1, &n2, &m);
    
    while(m--)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }
    
    int res = 0;
    for(int i = 1; i <= n1; ++i)
    {
        memset(st, 0, sizeof st);  // 如果不置为false，那么就不能要求匹配过的更换了
        if(find(i)) res++;
    }
    
    printf("%d\n", res);
    
    return 0;
}