【本科生机器学习】【Python】【北京航空航天大学】课题报告:支持向量机(Support Vector Machine, SVM)初步研究【下、实验部分(二)】)
说明:
(1)、仅供个人学习使用;
(2)、本科生学术水平有限,故不能保证全无科学性错误,本文仅作为该领域的学习参考。
实验原理部分见【上、原理部分】
实验一~实验三见【中、实验部分(一)】
实验内容(及结论)
四、实验四
1、实验描述: 非线性 SVM分类。
2、实验主要步骤:
(1)、 数据预处理流程:
加载卫星数据集:
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15) # 训练集
缩放特征:
polynomial_svm_clf = Pipeline([ # 使用多项式特征的SVM分类器
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()), # 特征缩放
("svm_clf", LinearSVC(C=10, loss="hinge", max_iter=5000))
])
(2)、 算法思想及步骤:
有很多数据集远不是线性可分离的。处理非线性数据集的方法之一是添加更多特征,比如多项式特征。某些情况下,这可能导致数据集变得线性可分离。
实验中,使用 Scikit-Learn 库来实现这个想法,创建一个包含 PolynomialFeatures 转换器的 Pipeline,然后是 StandardScaler 和 LinearSVC,并在训练集上训练该模型:
polynomial_svm_clf = Pipeline([ # 使用多项式特征的SVM分类器
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge", max_iter=5000))
])
polynomial_svm_clf.fit(X, y)
接下来,使用该模型对选定的5个样本点进行分类测试:
# 在测试集上测试模型:
print(polynomial_svm_clf.predict([[0.0, 0.0]])) # 1
print(polynomial_svm_clf.predict([[0.5, 1.0]])) # 2
print(polynomial_svm_clf.predict([[1.1, 0.6]])) # 3
print(polynomial_svm_clf.predict([[2.4, -0.3]])) # 4
print(polynomial_svm_clf.predict([[-0.7, -0.9]])) # 5
3、实验全部代码(使用Python):
# 实验四
# 非线性SVM分类器,在卫星数据集上进行测试
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
X, y = make_moons(n_samples=100, noise=0.15) # 训练集
polynomial_svm_clf = Pipeline([ # 使用多项式特征的SVM分类器
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge", max_iter=5000))
])
polynomial_svm_clf.fit(X, y)
# 在测试集上测试模型:
print(polynomial_svm_clf.predict([[0.0, 0.0]])) # 1
print(polynomial_svm_clf.predict([[0.5, 1.0]])) # 2
print(polynomial_svm_clf.predict([[1.1, 0.6]])) # 3
print(polynomial_svm_clf.predict([[2.4, -0.3]])) # 4
print(polynomial_svm_clf.predict([[-0.7, -0.9]])) # 5
4、实验结论
(1)、 生成的模型:
图9.使用多项式特征的SVM分类器
(2)、 在卫星数据集上进行测试:
模型对测试数据点的分类结果为:
[1], [0], [0], [1], [0]
对结果的解释:线性SVM分类器将样本特征 (x1,x2)=(0.5,1.0) 的样本点划为正方形类(即图9中深色区域),将样本特征 (x1,x2)=(0.0,0.0) 的样本点划为三角形类(即图9中浅色区域),其余样本点类似。
五、实验五
1、实验描述: 探究多项式内核。
2、实验主要步骤:
(1)、 数据预处理流程:同实验四。
(2)、 算法思想及步骤:
添加多项式特征实现起来非常简单,并且对所有的机器学习算法都非常有效。但问题是,如果多项式的阶数太低,则处理不了非常复杂的数据集。而高阶多项式则会创造出大量的特征,导致模型训练速度变得太慢。
使用SVM时,有一个数学技巧可以应用,这就是核技巧。它产生的结果就和添加了许多多项式特征一样,但实际上并不需要真的添加。这个技巧由SVC类来实现。
实验中,使用一个3阶多项式内核训练SVM分类器。
polynomial_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])
polynomial_svm_clf.fit(X, y)
为了研究多项式内核阶数对模型分类效果的影响,创建一个10阶分类器:
polynomial_svm_clf2 = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
])
polynomial_svm_clf2.fit(X, y)
用上述2个分类器对随机样本点进行分类测试:
# 用随机样本点测试模型,并将两个模型进行对比
# 期望输出:0, 1, 1, 0, 1
print(polynomial_svm_clf.predict([[0.5, 1.0]])) # 1
print(polynomial_svm_clf.predict([[0.0, 0.0]])) # 2
print(polynomial_svm_clf.predict([[1.9, 1.0]])) # 3
print(polynomial_svm_clf.predict([[0.5, 0.5]])) # 4
print(polynomial_svm_clf.predict([[0.69, 0.0]])) # 5
print()
# 期望输出:0, 1, 0, 1, 0
print(polynomial_svm_clf2.predict([[0.5, 1.0]])) # 1
print(polynomial_svm_clf2.predict([[0.0, 0.0]])) # 2
print(polynomial_svm_clf2.predict([[1.9, 1.0]])) # 3
print(polynomial_svm_clf2.predict([[0.5, 0.5]])) # 4
print(polynomial_svm_clf.predict([[0.69, 0.0]])) # 5
3、实验全部代码(使用Python):
# 实验五
# 非线性SVM分类器,在卫星数据集上进行测试
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
X, y = make_moons(n_samples=100, noise=0.15) # 训练集
polynomial_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])
polynomial_svm_clf.fit(X, y)
polynomial_svm_clf2 = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
])
polynomial_svm_clf2.fit(X, y)
# 用随机样本点测试模型,并将两个模型进行对比
# 期望输出:0, 1, 1, 0, 1
print(polynomial_svm_clf.predict([[0.5, 1.0]])) # 1
print(polynomial_svm_clf.predict([[0.0, 0.0]])) # 2
print(polynomial_svm_clf.predict([[1.9, 1.0]])) # 3
print(polynomial_svm_clf.predict([[0.5, 0.5]])) # 4
print(polynomial_svm_clf.predict([[0.69, 0.0]])) # 5
print()
# 期望输出:0, 1, 0, 1, 0
print(polynomial_svm_clf2.predict([[0.5, 1.0]])) # 1
print(polynomial_svm_clf2.predict([[0.0, 0.0]])) # 2
print(polynomial_svm_clf2.predict([[1.9, 1.0]])) # 3
print(polynomial_svm_clf2.predict([[0.5, 0.5]])) # 4
print(polynomial_svm_clf.predict([[0.69, 0.0]])) # 5
4、实验结论
(1)、 生成的模型:
图10.多项式内核的SVM分类器
解释:左图为3阶多项式内核的SVM分类器,而右图为10阶多项式内核的SVM分类器。可以看出,与左图相比,右图明显存在过拟合的现象。得出初步结论:如果模型过拟合,应该降低多项式阶数;如果模型欠拟合,则应该适当提升多项式阶数。
(2)、 对随机样本点进行分类测试:
第1个模型的分类结果:
[0], [1], [1], [0]
第2个模型的分类结果:
[0], [1], [0], [1]
对结果的解释:
对于距离决策边界较远的样本点,即 (x1,x2)=(0.5,1.0) 以及 (x1,x2)=(0.0,0.0) ,两个多项式核的SVM分类器输出类别相同,分别为正方形类和三角形类;然而,对于决策边界附近的样本点,例如 (x1,x2)=(1.99,1.0) ,3阶多项式内核的SVM分类器将其归入三角形类,但10阶多项式内核的SVM分类器将其归入正方形类;对于 (x1,x2)=(0.5,0.5) ,3阶多项式内核的SVM分类器将其归入正方形类,但10阶多项式内核的SVM分类器将其归入三角形类。
六、实验六
1、实验描述: 线性SVM回归。
2、实验主要步骤:
(1)、 数据预处理流程:
线性SVM回归使用随机生成的 线性数据集(X, y) 作为训练集:
# 随机生成线性数据集作为训练集
X = 2 * np.random.rand(100, 1)
y = (4 + 3 * X + np.random.randn(100, 1)).reshape(100, )
SVM算法不仅支持(线性和非线性)分类,而且还支持(线性和非线性)回归。线性SVM回归要做的是让尽可能多的实例位于街道上,同时限制间隔违例(也就是不在街道上的实例)。街道的宽度由超参数ε控制。当ε较大时,线性SVM回归模型的间隔较大;当ε较小时,线性SVM回归模型的间隔较小。
在间隔内添加更多的实例不会影响模型的预测,所以这个模型被称为 “ε-不敏感” 。
本实验中,使用 Scikit-Learn 库中的 LinearSVR 类来执行线性SVM回归,将ε的值分别设定为 1.5 和 0.5 ,观察生成的回归模型的区别:
# SVM回归
svm_reg1 = LinearSVR(epsilon=1.5, max_iter=5000)
svm_reg2 = LinearSVR(epsilon=0.5, max_iter=5000)
svm_reg1.fit(X, y)
svm_reg2.fit(X, y)
在测试集上测试模型,对给定的x, 观察模型对Y的预测值:
# 测试集
X_test = np.array([[0], [0.5], [1], [1.5], [2], [2.5], [3], [3.5], [4], [4.5], [5]])
# 在测试集上测试模型效果
print(svm_reg1.predict(X_test))
print(svm_reg2.predict(X_test))
4、实验结论
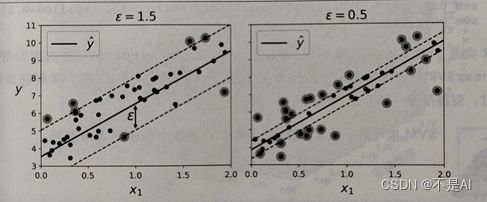
(1)、 生成的模型:
图11.SVM回归模型图示
解释:超参数ε代表拟合宽度在垂直方向上投影的长度。可以看到,左图(ε=1.5)的模型间隔更大,泛化效果更好;右图(ε=0.5)的模型间隔更小,间隔违例更少。
(2)、 模型的测试结果:
2个模型分别在测试集上的输出:
(3)、 评估模型:
在数据集
# 评估数据集
X_eval = np.array([[0], [0.2], [0.4], [0.6], [0.8], [1], [1.2], [1.4], [1.6], [1.8], [2]])
上对模型进行评估。为了与之前拟合的直线x坐标范围匹配,故选择 [0,2] 内均匀分布的11个数据点。
拟合结果:
图12. SVM回归模型评估结果
由上图可以看出,2个模型的误差均在允许范围内。
实验部分到此结束。