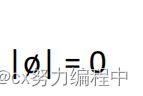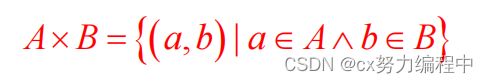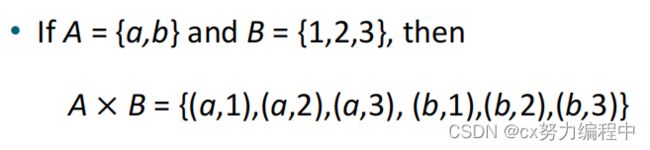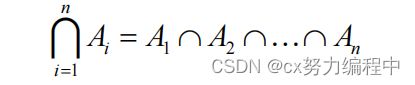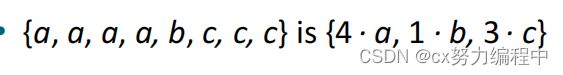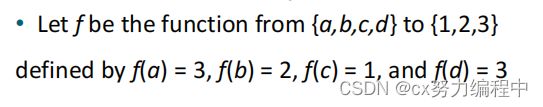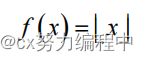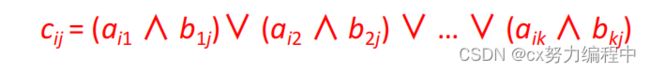离散数学期末复习（2）: 集合、函数、序列、矩阵

目录

2.1 Sets (集合)

1.特殊集合

2.一些概念

2.2 Set Operations (集合运算)

一. 集合间的概念

 1.并集（Union）

2.交集（Intersection）

3.补集（Complement）

 4.差集（Difference）

 二. 定律

 三. 多重集

1. 概念

2. 多重集的并集

 3.多重集的交集

 4.多重集的差集

 5.多重集合集

2.3 Functions (函数)

1.函数的三种理解

 2.单射（injection） 

3.满射（surjections）

4.双射（Bijections）

 5.复合函数（传递的特点）

 6.上取整和下取整函数

2.4 Sequences and Summations (序列与求和)

2.5 Cardinality of Sets (集合的基数)

1. 基数和函数关系

2. 可数

2.6 Matrices (矩阵)

1.基本概念

2.矩阵运算（普通运算）

（1）加法：

（2）乘法：

（3）单位矩阵

 （4）转置矩阵：行列互换

（5）对称矩阵：当矩阵A里面的aij = aji的时候，矩阵A是对称矩阵

 3.逻辑运算

（1）并

（2）交

 （3）布尔积   

---

2.1 Sets (集合)

没什么好说的，高中概念

1.特殊集合

2.一些概念

（1）区间

（2）全集空集

注意一点：空集和包含空集的集合不一样‘

（3）子集

真子集：

真子集的韦恩图 

子集： 

 （4）基数

一个有限集A的基数是A中元素的数量，用|A|表示。

注意：空集的基数为0，但是包含空集的集合的基数是1

 （5）幂集

集合A的所有子集的集合，记为P (A)，称为A的幂集

6.元组

有序的n元组（1,2，.....，）是有序的集合，它的第一个元素是1, 第二个元素是2，以此类推，直到最后一个元素.

7.笛卡尔积（Cartesian Product）

集合A和集合B的笛卡尔积 = A ✖ B

例子：

 

 笛卡尔积A×B的一个子集R被称为从集合A到集合B的关系

多个集合的笛卡尔积

2.2 Set Operations (集合运算)

一. 集合间的概念

 1.并集（Union）

并集相当于逻辑运算里面的或 

2.交集（Intersection）

 不相交的两个集合的交集 = ∅

3.补集（Complement）

 4.差集（Difference）

 二. 定律

第二德摩根律证明

 还可以用集合生成器来证明

 三. 多重集

1. 概念

一个多重集是一个元素的无序集合，其中一个元素可以作为一个成员多次出现

这里的4  1  3被称为重数

2. 多重集的并集

就是找出P和Q相同元素的重数最大值再乘上元素组合成的新集合

 

 3.多重集的交集

找出P和Q二者共同元素重数最小值再乘上元素组成的新集合

 

 4.多重集的差集

找出P和Q二者共同元素重数相减，接着与0比较得出而这最大值，得出的最大值与元素相乘组合成新集合

 5.多重集合集

找出P和Q二者共同元素重数相加再与元素相乘组合成新集合

2.3 Functions (函数)

1.函数的三种理解

第一种：分配    f: A-->B 把A里的元素分配给B

第二种：关系    

第三种：映射

f:  A-->B说明f是A到B的一个映射，此时A是f的定义域，B是f的陪域

 

 f的值域是A中f下所有点的图像的集合，用f (A)表示

 2.单射（injection） 

 一对一函数，x不同则y不同

即：没有一个x对应两个y，也没有一个y有对应两个x

一般是少射向多，而且有元素没有匹配到

3.满射（surjections）

对任意b，存在a满足f(a) = b

即：值域y是满的，每个y都有x对应，不存在某个y没有x对应的情况 

一般是多射向少，多的元素可能射向少里面的同一个元素，但不存在少里面的元素没对应的情况

4.双射（Bijections）

既是满射，也是单射

即：每个y都有x对应，而且都是一一对应

---

 例子

这里的f是满射吗？

答案是对的。 因为陪域{1，2，3}里面的三个元素都是定义域{a,b,c,d}里面的像

如果陪域改成{1，2，3，4}就不是满射

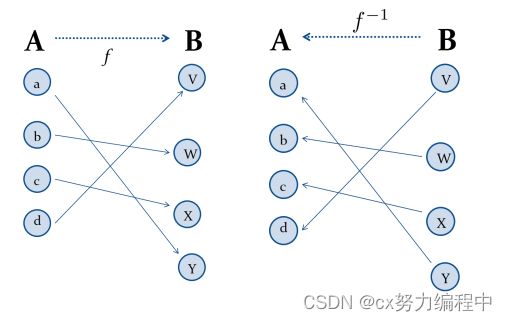
注意：函数f存在反函数是函数f是双射的充要条件

 5.复合函数（传递的特点）

 6.上取整和下取整函数

上取整

 下取整

 

2.4 Sequences and Summations (序列与求和)

 只有这个要记

2.5 Cardinality of Sets (集合的基数)

1. 基数和函数关系

集合A的基数等于集合B的基数，表示为|A| = |B|当且仅当a到B存在双射

如果从A到B有单射，那么A|≤|B|

2. 可数

 当且仅当可以在一个序列中列出该集合的元素（由正整数组成）时，一个无限集合S是可数的

比如：f(x) = 2x 这是一个无线集合，但是可数

证明：正有理数是可数的

2.6 Matrices (矩阵)

1.基本概念

（1）一个m行n列的矩阵可以写成m×n矩阵

 当行和列相等时，这个矩阵被称为方阵

（2）元素

2.矩阵运算（普通运算）

（1）加法：

对应位置元素相加就行

（2）乘法：

A横行×B纵列 

注意：AB≠BA

（3）单位矩阵

 （4）转置矩阵：行列互换

（5）对称矩阵：当矩阵A里面的aij = aji的时候，矩阵A是对称矩阵

如：

 3.逻辑运算

（1）并

A和B的合并，用A∨B表示，是aij∨bij的零1矩阵。

（2）交

A和B的相交，用A∧B表示，是aij∧bij的零1矩阵。

 

 （3）布尔积   AB 

  

 同一个矩阵的布尔积