【Chapter 2】Asympototic Analysis
Θ记号
对于一个给定的函数 g ( n ) g(n) g(n),用 Θ ( g ( n ) ) \Theta(g(n)) Θ(g(n))来表示以下函数的集合: Θ ( g ( n ) ) = { f ( n ) : 存在正常量 c 1 , c 2 和 n 0 , 使得对所有 n ≥ n 0 , 有 0 ≤ c 1 g ( n ) ≤ f ( n ) ≤ c 2 g ( n ) } \Theta(g(n))=\{f(n): 存在正常量c_1, c_2和n_0, 使得对所有n\geq{n_0}, 有0\leq{c_1}g(n)\leq{f(n)}\leq{c_2}g(n)\} Θ(g(n))={f(n):存在正常量c1,c2和n0,使得对所有n≥n0,有0≤c1g(n)≤f(n)≤c2g(n)}。若存在正常量(正的常数量) c 1 c_1 c1和 c 2 c_2 c2,使得对于足够大的 n n n,函数 f ( n ) f(n) f(n)能“夹入” c 1 g ( n ) c_1g(n) c1g(n)与 c 2 g ( n ) c_2g(n) c2g(n)之间,则 f ( n ) f(n) f(n)属于集合 Θ ( g ( n ) ) \Theta{(g(n))} Θ(g(n))。
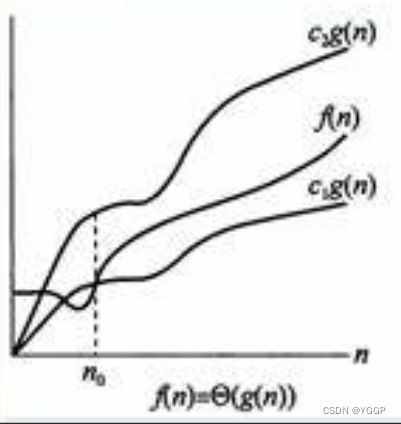
上图给出了f(n)与g(n)的直观画面,其中 f ( n ) = Θ ( g ( n ) ) f(n)=\Theta(g(n)) f(n)=Θ(g(n))。对于在 n 0 n_0 n0及其右边的所有值, f ( n ) f(n) f(n)的值位于或高于 c 1 g ( n ) c_1g(n) c1g(n)且位于或低于 c 2 g ( n ) c_2g(n) c2g(n)。
举个例子,使用形式化的符号来证明 1 2 n 2 − 3 n = Θ ( n 2 ) {1\over2}n^2-3n=\Theta(n^2) 21n2−3n=Θ(n2)成立:
对于正常量 c 1 , c 2 , n 0 c_1, c_2, n_0 c1,c2,n0,使得对所有 n ≥ n 0 n\geq{n_0} n≥n0有:
c 1 n 2 ≤ 1 2 n 2 − 3 n ≤ c 2 n 2 c_1n^2\leq{{1\over2}n^2-3n}\leq{c_2n^2} c1n2≤21n2−3n≤c2n2
用 n 2 n^2 n2除以上式,得:
c 1 ≤ 1 2 − 3 n ≤ c 2 c_1\leq{1\over2}-{3\over{n}}\leq{c_2} c1≤21−n3≤c2
通过选择任何常量 c 2 ≥ 1 2 c_2\geq{1\over2} c2≥21,可以使右边的不等式对任何 n ≥ 1 n\geq1 n≥1成立;同样,通过选择任何常量 c 1 ≤ 1 14 c_1\leq{1\over{14}} c1≤141,可以使左边的不等式对任何 n ≥ 7 n\geq7 n≥7的值成立。因此,通过选择 c 1 = 1 14 , c 2 = 1 2 , n 0 = 7 c_1={1\over{14}}, c_2={1\over2}, n_0=7 c1=141,c2=21,n0=7,即可证明 1 2 n 2 − 3 n = Θ ( n 2 ) {1\over2}n^2-3n=\Theta(n^2) 21n2−3n=Θ(n2)成立。
(选择 c 2 = 1 2 c_2={1\over2} c2=21需要满足 n ≥ 1 n\geq1 n≥1,而 n 0 = 7 n_0=7 n0=7显然是满足 n ≥ 1 n\geq1 n≥1的)
O记号和Ω记号
Θ \Theta Θ记号渐进地给出一个函数的上界和下界,函数则被夹在上界和下界之间,当只有一个渐进上界时,使用 O O O记号;只有一个渐进下界时,使用 Ω \Omega Ω记号。
o记号和ω记号
O O O和 Ω \Omega Ω给出的是渐进紧确界,而小写字母符号中的 o o o和 ω \omega ω给出的则是非渐进紧确界,此时对于 o o o和 ω \omega ω两种记号,不等式当中的等号不再成立。
算法导论中与Θ有关的练习题
由于上课时明确指出,考试的第一题是使用纯符号进行一个有关 Θ \Theta Θ记号的证明题,并且这个证明题是出自于算法导论课后题的,因此使用博客的方式对复习过程进行记录。算法导论课后题的答案参考自:https://zhuanlan.zhihu.com/p/35850085。
3.1-1
题目描述: 假设 f ( n ) f(n) f(n)和 g ( n ) g(n) g(n)都是渐进非负函数。使用 Θ \Theta Θ记号的基本定义来证明 m a x ( f ( n ) , g ( n ) ) = Θ ( f ( n ) + g ( n ) ) max(f(n), g(n))=\Theta(f(n)+g(n)) max(f(n),g(n))=Θ(f(n)+g(n))。
解答:
对于渐进非负函数 f ( n ) , g ( n ) f(n), g(n) f(n),g(n),有:
∃ n 1 , n 2 : f ( n ) ≥ 0 , n ≥ n 1 ; g ( n ) ≥ 0 , n ≥ n 2 \exists{n_1, n_2}: f(n)\geq0, n\geq{n1};\ g(n)\geq0, n\geq{n_2} ∃n1,n2:f(n)≥0,n≥n1; g(n)≥0,n≥n2
令 n 0 = m a x ( n 1 , n 2 ) n_0=max(n_1, n_2) n0=max(n1,n2),针对 n ≥ n 0 n\geq{n_0} n≥n0,有下述不等式成立:
f ( n ) ≤ m a x ( f ( n ) , g ( n ) ) f(n)\leq{max(f(n), g(n))} f(n)≤max(f(n),g(n))
g ( n ) ≤ m a x ( f ( n ) , g ( n ) g(n)\leq{max(f(n), g(n)} g(n)≤max(f(n),g(n)
f ( n ) + g ( n ) 2 ≤ m a x ( f ( n ) , g ( n ) ) {{f(n)+g(n)}\over2}\leq{max(f(n), g(n))} 2f(n)+g(n)≤max(f(n),g(n))
m a x ( f ( n ) , g ( n ) ) ≤ f ( n ) + g ( n ) {max(f(n), g(n))}\leq{f(n)+g(n)} max(f(n),g(n))≤f(n)+g(n)
将第三个和第四个不等式进行组合,得到:
f ( n ) + g ( n ) 2 ≤ m a x ( f ( n ) , g ( n ) ) ≤ f ( n ) + g ( n ) {{f(n)+g(n)}\over2}\leq{max(f(n), g(n))}\leq{f(n)+g(n)} 2f(n)+g(n)≤max(f(n),g(n))≤f(n)+g(n)
综上所示,存在当 c 1 = 1 2 , c 2 = 1 , n 0 = m a x ( n 1 , n 2 ) c_1={1\over2}, c_2=1, n_0=max(n_1, n_2) c1=21,c2=1,n0=max(n1,n2)使得上述不等式成立。
原命题得证。
3.1-2
题目描述: 证明:对任意实常量 a a a和 b b b,其中 b > 0 b>0 b>0,有: ( n + a ) b = Θ ( n b ) (n+a)^b=\Theta(n^b) (n+a)b=Θ(nb)。
解答:
根据二项式定理,对 ( n + a ) b (n+a)^b (n+a)b进行展开:
( n + a ) b = C 0 b n b a 0 + C 1 b n b − 1 a 1 + . . . + C b b n 0 a b (n+a)^b=C^b_0n^ba^0+C^b_1n^{b-1}a^1+...+C^b_bn^0a^b (n+a)b=C0bnba0+C1bnb−1a1+...+Cbbn0ab
此外,对于任何多项式,在 x ≥ 1 x\geq1 x≥1的前提下,有下述不等式成立:
a 0 x 0 + a 1 x 1 + . . . + a n x n ≤ ( a 0 + a 1 + . . . + a n ) x n a_0x^0+a_1x^1+...+a_nx^n\leq{(a_0+a_1+...+a_n)}x^n a0x0+a1x1+...+anxn≤(a0+a1+...+an)xn
又,根据二项式定理,有: C 0 b + C 1 b + . . . + C b b = 2 b C^b_0+C^b_1+...+C^b_b=2^b C0b+C1b+...+Cbb=2b(令 ( 1 + x ) n (1+x)^n (1+x)n展开后x为1即可得)成立;
综上,有:
C 0 b n b ≤ C 0 b n b a 0 + C 1 b n b − 1 a 1 + . . . + C b b n 0 a b ≤ 2 b n b C^b_0n^b\leq{C^b_0n^ba^0+C^b_1n^{b-1}a^1+...+C^b_bn^0a^b}\leq{2^b}n^b C0bnb≤C0bnba0+C1bnb−1a1+...+Cbbn0ab≤2bnb
即 ( n + a ) b = Θ ( n b ) (n+a)^b=\Theta(n^b) (n+a)b=Θ(nb)得证。
3.1-5
题目描述: 证明定理3.1:对任意两个函数 f ( n ) f(n) f(n)和 g ( n ) g(n) g(n),我们有 f ( n ) = Θ ( g ( n ) ) f(n)=\Theta(g(n)) f(n)=Θ(g(n)),当且仅当 f ( n ) = O ( g ( n ) ) 且 f ( n ) = Ω ( g ( n ) ) f(n)=O(g(n))且f(n)=\Omega(g(n)) f(n)=O(g(n))且f(n)=Ω(g(n))。
解答:
对于 f = Θ ( g ( n ) ) f=\Theta(g(n)) f=Θ(g(n)),有:
0 ≤ c 1 g ( n ) ≤ f ( n ) ≤ c 2 g ( n ) , n > n 0 0\leq{c_1}g(n)\leq{f(n)}\leq{c_2}g(n), n\gt{n_0} 0≤c1g(n)≤f(n)≤c2g(n),n>n0
而对于 f ( n ) = Ω ( g ( n ) ) f(n)=\Omega(g(n)) f(n)=Ω(g(n))和 f ( n ) = O ( g ( n ) ) f(n)=O(g(n)) f(n)=O(g(n)),有:
0 ≤ c 3 g ( n ) ≤ f ( n ) , n ≥ n 1 0\leq{c_3}g(n)\leq{f(n)}, n\geq{n_1} 0≤c3g(n)≤f(n),n≥n1
0 ≤ f ( n ) ≤ c 4 g ( n ) , n ≥ n 2 0\leq{f(n)}\leq{c_4}g(n), n\geq{n_2} 0≤f(n)≤c4g(n),n≥n2
取 n 3 = m a x ( n 1 , n 2 ) n_3=max(n_1, n_2) n3=max(n1,n2),并合并不等式,得到:
0 ≤ c 3 g ( n ) ≤ f ( n ) ≤ c 4 g ( n ) , n ≥ n 3 0\leq{c_3}g(n)\leq{f(n)}\leq{c_4}g(n), n\geq{n_3} 0≤c3g(n)≤f(n)≤c4g(n),n≥n3
它与 Θ \Theta Θ的定义相同,原命题得证。
3.1-6
题目描述: 证明:一个算法的运行时间为 Θ ( g ( n ) ) \Theta(g(n)) Θ(g(n))当且仅当其最坏情况运行时间为 O ( g ( n ) ) O(g(n)) O(g(n)),且其最好情况运行时间为 Ω ( g ( n ) ) \Omega(g(n)) Ω(g(n))。
解答:
使用 T w T_w Tw代表最坏情况运行时间,而使用 T b T_b Tb代表最好情况运行时间,可以得到:
0 ≤ c 1 g ( n ) ≤ T b ( n ) , n > n b 0\leq{c_1}g(n)\leq{T_b(n)}, n\gt{n_b} 0≤c1g(n)≤Tb(n),n>nb
0 ≤ T w ( n ) ≤ c 2 g ( n ) , n > n w 0\leq{T_w}(n)\leq{c_2g(n)}, n\gt{n_w} 0≤Tw(n)≤c2g(n),n>nw
组合上述不等式,得到:
0 ≤ c 1 g ( n ) ≤ T b ( n ) ≤ T w ( n ) ≤ c 2 g ( n ) , n > m a x ( n b , n w ) 0\leq{c_1}g(n)\leq{T_b}(n)\leq{T_w}(n)\leq{c_2}g(n), n\gt{max(n_b, n_w)} 0≤c1g(n)≤Tb(n)≤Tw(n)≤c2g(n),n>max(nb,nw)
由于运行时间介于 T b T_b Tb和 T w T_w Tw之间,并且上式正是 Θ \Theta Θ记号的定义,因此原命题成立,证毕。
3.2-8
题目描述: 证明: k l n k = Θ ( n ) klnk=\Theta(n) klnk=Θ(n)蕴含着 k = Θ ( n l n n ) k=\Theta({n\over{lnn}}) k=Θ(lnnn)
解答:
首先根据 Θ \Theta Θ的对称性,得到:
k l n k = Θ ( n ) → n = Θ ( k l n k ) klnk=\Theta(n) \rightarrow n=\Theta(klnk) klnk=Θ(n)→n=Θ(klnk)
现在寻找 l n n lnn lnn:
l n n = Θ ( l n ( k l n k ) ) = Θ ( l n k + l n ( l n k ) ) = Θ ( l n k ) lnn=\Theta(ln(klnk))=\Theta(lnk+ln(lnk))=\Theta(lnk) lnn=Θ(ln(klnk))=Θ(lnk+ln(lnk))=Θ(lnk)
将上面两个式子相除,构造 n l n n {n\over{lnn}} lnnn,得到:
n l n n = Θ ( k l n k ) Θ ( l n k ) = Θ ( k l n k l n k ) = Θ ( k ) {n\over{lnn}}={{\Theta(klnk)}\over{\Theta(lnk)}}=\Theta({{klnk}\over{lnk}})=\Theta(k) lnnn=Θ(lnk)Θ(klnk)=Θ(lnkklnk)=Θ(k)
再由 Θ \Theta Θ的对称性,得到 k = Θ ( n l n n ) k=\Theta({n\over{lnn}}) k=Θ(lnnn)。
3-4 h.
题目描述: 证明: f ( n ) + o ( f ( n ) ) = Θ ( f ( n ) ) f(n)+o(f(n))=\Theta(f(n)) f(n)+o(f(n))=Θ(f(n))
解答:
对于 o ( f ( n ) ) o(f(n)) o(f(n)),令 g ( n ) = o ( f ( n ) ) g(n)=o(f(n)) g(n)=o(f(n)),有:
0 ≤ g ( n ) ≤ c f ( n ) 0\leq{g(n)}\leq{cf(n)} 0≤g(n)≤cf(n)
因此,有下述不等式成立:
0 ≤ c 1 f ( n ) ≤ f ( n ) + g ( n ) ≤ c 2 f ( n ) 0\leq{c_1}f(n)\leq{f(n)+g(n)}\leq{c_2}f(n) 0≤c1f(n)≤f(n)+g(n)≤c2f(n)
选取 c 1 = 1 , c 2 = c + 1 c_1=1, c_2=c+1 c1=1,c2=c+1可以使原命题成立。