2024.1.23 GNSS 零散知识 学习笔记
1.天线种类
2.接收机
2.四大导航系统的介绍
3.卫星高度与轨道卫星种类
4.GNSS有哪些应用
5.在空间保持静⽌或匀速直线运动(⽆加速度)的坐标系称为惯性坐标系。
6.地⼼惯性坐标系实际上并没有满⾜能成为惯性坐标系的条件：
⾸先，地球及其质⼼都在围绕太阳做⾮匀速直线运动;
其次，地球⾃转轴在空间的⽅向不是固定不变的，⽽是存在⼀种⾮常复杂的运动。
地心惯性坐标系(ECI坐标系)的定义：
常简称为地⼼惯性 (Earth Centered Inertial, ECI)坐标系，其中下标 I 的含义为惯性。该坐标系以指向北极的地球⾃转轴为Z轴，X轴指向春分点，⽽X、 Y和Z三轴⼀起构成右⼿直⻆坐标系统。
下图是⼀个坐标中⼼建⽴在地球质⼼点O的地⼼直⻆惯性坐标系
7.为什么要建立惯性坐标系？
因为GNSS卫星轨道在惯性系中服从⽜顿运动定律和万有引⼒定律，所以在地⼼惯性系中描述卫星运⾏轨道相当⽅便。
8.岁差和章动是对地球自转轴的作用。
岁差：春分点沿着⻩道 缓慢地向西移动；
章动：在绕北⻩极做圆周旋转的同时，地球⾃转轴还存在⼀种称为章动的局部⼩幅旋转。
9.为什么要建立协议天球坐标系？
由于在岁差和章动的影响下，瞬时天球坐标系的坐标轴的指向在不断的变化。在这种⾮惯性坐标系统中，不能直接根据⽜顿⼒学定 律来研究卫星的运动规律。为了建⽴⼀个与惯性坐标系相接近的坐标系，通常选择某⼀时刻作为标准历元，并将此刻地球的瞬时⾃转轴（指向北极）和地⼼⾄瞬时春分点的⽅向，经过瞬时的岁差和章动改正后，分别作为z轴和x轴的指向。由此所构成的空间固定 坐标系，称为协议天球坐标系。
10.为什么要建立地球坐标系？为什么地球坐标系也称为地固坐标系、地心地固坐标系？
我们在惯性系中描述卫星运动，但惯性系随着地球⾃转⽽变化，这对于我们描述地⾯上的物体带来极⼤的不便。
主要目的是更方便地描述地面上的物体。
与惯性坐标系不同，地球坐标系固定在地球上⽽随地球⼀起在空间做公转和⾃转运动，所以它⼜称地固坐标系。⼀般我们将坐标原 点选择为地⼼，所以⼜称为地⼼地固坐标系（Earth Centered Earth Fixed, ECEF）。
11.地心地固坐标系分为哪几种类型？
地心直角坐标系和地心大地坐标系。
12.地心地固直角坐标系的定义？
地⼼地固直⻆坐标系通常以地⼼O作为坐标原点，其Z轴指向地球北极，X轴指向英国伦敦处的格林尼治⼦午⾯与地球⾚道的交点， ⽽X、Y和Z三轴⼀起构成右⼿直⻆坐标系。
13.什么是极移？极移对GNSS会造成什么样的影响？
极移是和地球南北两极点的变化有关，进而会影响地心地固直角坐标系的Z轴指向。
事实上，地球南北两极点在地球表⾯以每年⼏⽶的速度⼤致沿⼀个半径约⼗⼏⽶的⼩圆移动，这种现象通常称为极移。
地极移动使地球⾃转轴和地⼼直⻆坐标系⼀起相对地球移动，这也会引起地球上固定点的地⼼直⻆坐标不再固定，给实际⼯作带来许多困难。
14.地⼼地固直⻆坐标系的 Z 轴与地球⾃转轴重合并指向北极，然⽽地球⾃转轴相对于地球并不是固定的。
15.什么是协议地极(CTP)？为什么要设置协议地极？什么是协议地球坐标系？
为了克服极移带来的困难，国际天⽂学联合会(IAU)和国际⼤地测量学协会(IAG)于1967 年建议将 1900 年⾄ 1905 年间的地极实际位置的平均值作为基准点，⽽这个在地球体上固定的地极基准点通常称为协议地极(CTP)，相应的⾚道⾯称为协议⾚道⾯。
以协议地极为基准点⽽建⽴的地球坐标系称为协议地球坐标系。
16.其实我们⽇常接触到的GNSS系统都是采⽤的协议地球坐标系，⽽不是⽆数个不同瞬间的⾮协议坐标系,所以我们以后只考虑协议地 球坐标系并且在不引起混淆的情况下，我们通常省略“协议”两字。
17.ITRF是由国际地球自转(及参考系统)服务(IERS)负责建立、维持的一个地心直⻆坐标系，它是国际公认的最为精确的全球参考框架。
由于ITRF的基准站考虑地球板块和潮汐等这些随时间变化的影响因素，因而ITRF会不断更新，例如ITRF2005是其中的一版。
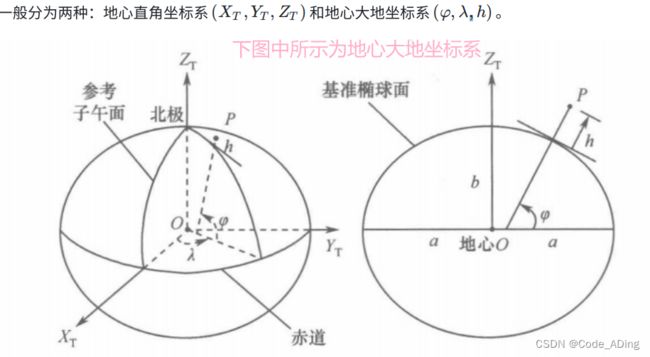
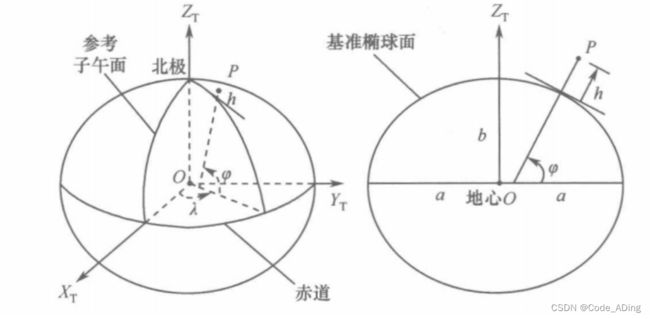
18.大地坐标系相关知识
大地坐标系是一个最为广泛应用的地球坐标系，它通过给出一点的大地纬度、大地经度和大地高度而更加直观地告诉我们该点在地球中的位置，故它又称纬经高(LLA)坐标系。（纬度、经度、高程）。
为了给出高度值,大地坐标系首先需要定义一个与地球几何最吻合的椭球体来代替表面凹凸不平的地球，这个椭球体被称为基准椭球体。
19.站心坐标系相关知识
站心坐标系以某用戶接收机在某时所处的位置点P为坐标原点，三个坐标轴分别是相互垂直的东向、北向和天向，因而站心坐标系又称东北天(ENU)坐标系。也有使用北东地(NED)作为当地水平坐标系。
下图形象地给出了站心坐标系的坐标enu是如何得到的：
20.GPS卫星的位置在时间过程中是变化的，因此在给定GPS卫星的位置坐标时，必须给出相应的瞬时时刻。
21.GPS定位的一般过程是什么？
GPS定位是通过GPS接收机测量和处理GPS卫星发射的信号，来确定观测站(即GPS接收机)至卫星的距离，进而确定观测站的位置。
而由观测站至卫星的距离的测定，是通过由卫星到测站的信号传播时间的精确测定再计算出来的，若要求上述距离误差小于1cm，则信号传播时间的测定误差，应不超过3×10-11s。
22.时间一般由参考框架和表示方法组成。比如我们日常生活中的一个时刻2023年07月01日12:00:00，是指在UTC时间框架下的公历（格里高利历）表示方法
23.GPS时间系统在标示时间时采用GPS周和周秒来标示GPS系统时间。所采用的最大时间单位为周（Week，即604800秒），其标示时间的方法是从1980年1月6日0时开始起算的周数（Week Number，WN）加上被称为周内时间（Time of Week，TOW）(周内秒)的从每周周六/周日子夜开始起算的秒数。在GPS卫星所发送的导航电文中，时间信息的标示就是采用这样的形式。
也就是说，GPS卫星在瞬时时刻发送出导航电文，那么在导航电文中会用GPS周和周内秒来表示GPS卫星系统的发送出导航电文的瞬时时刻。同理，其他卫星导航系统的时间标识也是相同做法。
一般在多系统导航电文中，在程序中一般要先进行时间系统的统一，通常都以GPS时间作为基准，其他的卫星导航系统会转换为GPST的时间表示方法，这样就实现了时间基准的统一。
24.常用的时间表示方法
公历：日常生活中使用的时间
25.电磁波测距原理介绍
测绘用的全站仪就是使用的电磁波测距原理。
测距仪、反光棱镜
1.卫星信号有哪几种？
第一种：载波。
可运载调制信号的高频振荡波称为载波。在无线电通信中,为了更好地传送信息,我们往往将这些信息调制在高频的载波上,然后再将这些调制波播发出去,而不是直接发射这些信息。
第二种：测距码。
测距码是用于测定从卫星至接收机间的距离的二进制码。
GPS卫星中所用的测距码从性质上讲属于伪随机噪声码。它们看似一组杂乱无章的随机噪声码,其实是按照一定规律编排起来的、可以复制的周期性的二进制序列，且具有类似于随机噪声码的自相关特性。
第三种：导航电文 / 数据码
导航电文是由GPS卫星向用戶播发的一组反映卫星在空间的位置、卫星的工作状态、卫星钟的修正参数、电离层延迟修正参数等重要数据的二进制代码，也称数据码(D码)。
总结：载波调制在C/A码上，C/A(测距码的一种，测距码还有P码等)调制在导航电文(数据码/D码)上，最终通过导航电文发送给用户。
2.导航电文中的观测值类型包括：伪距观测值、载波观测值、多普勒观测值等。
3.伪距观测值：实际上是测量GPS卫星发射的测距码信号（C/A码或P码）到达用戶接收机天线的电磁波传播时间。因此，这种观测方法也称为时间延迟测量。
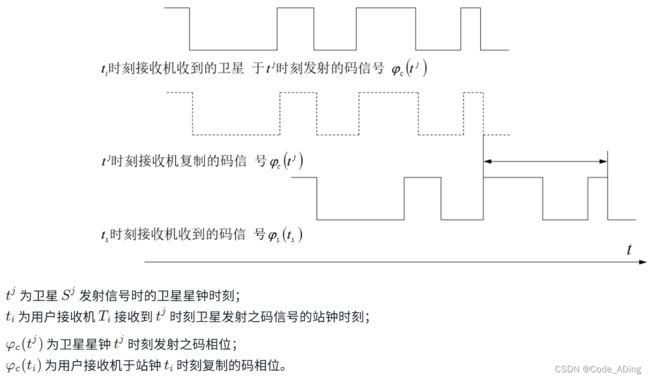由于卫星的星钟和接收机的站钟不可能完全同步，同时无线电信号经过电离层和对流层时由于折射的影响也均有附加延迟，所以实际测量得到的距离不是真实的距离，而是含有误差的伪距，即伪距观测值（从相关测站的观测值文件中直接获得相关的观测值）。
接收机复制的测距码和接收到的卫星发射的测距码在时间延迟器的作用下相关时（对⻬时），根据经验，相关精度约为码元宽度的1%。对于C/A码来讲，由于其码元宽度约为293m，所以其观测精度为2.9m。而对于P码来讲，其码元宽度是C/A码码元宽度的1/10(29.3m)，故其测量精度也就比C/A码的测码精度高10倍，为0.29m。因此，有时也将C/A码称为粗码，P码称为精码。
但对于粗码来说，采用窄相关间隔(Narrow Correlator Spacing)技术后测距精度可达分米级，与精码的测距精度大体相当。
对应观测值文件中的P1 P2和C1 C2，一般我们计算时优先考虑使用P1 P2
4.载波观测值：
以GPS为例，对L1载波来讲，测距精度为0.19m，对L2载波来说，测距经度为0.24m。
从相关测站的观测值文件中可以读取相应的载波观测量的值。
在观测值文件中对应L1 L2
5.多普勒观测值
波长 等于 光速 除以 频率。
对应观测值文件中的D1 D2
6.在GNSS定位中观测值与卫星、接收机有关的误差 图示
7.卫星轨道误差
由卫星星历所给出的卫星在空间的位置及运动速度与卫星的实际位置及运动速度之差称为卫星轨道误差。
通过广播星历计算得出的卫星位置和运动速度不是绝对准确的，不可避免地含有误差，称之为卫星轨道误差。
GNSS卫星的广播星历是由全球定位系统的地面控制部分所确定和提供的，经GNSS卫星向全球所有用戶公开播发的一种预报星历，其精度较差，一般广播星历轨道的精度在米级。
8.卫星钟 / 接收机钟误差
由卫星星历所给出的卫星钟与标准时间之差称为卫星钟误差；同理，接收机钟误差为接收机钟面时与标准时间之差称为接收机钟误差。
9.天线相位中心误差
卫星天线和接收机天线的天线相位中心既不是一个物理点，也不是一个稳定的点，对任一天线，天线相位中心都会随着来自卫星信号方向的变化而变化。
观测值测量的是卫星瞬时天线相位中心与接收机瞬时天线相位中心之间的距离。
关于天线相位中心有两个概念：
瞬时天线相位中心：天线的相位中心会随着信号频率、方位⻆、高度⻆等变化，在给定信号频率、方位⻆、高度⻆的情况下所确定的天线相位中心称为瞬时天线相位中心；
平均天线相位中心：由于天线相位中心会随着频率、方位⻆、高度⻆甚至天线罩变化，通常不同条件下的天线相位中心位置取平均值作为平均天线相位中心。
天线相位中心的误差由两部分组成:
一部分是相对于天线物理参考点（ARP）的平均相位中心偏差（PCO），
另一部分是与高度⻆和方位⻆有关的瞬时相位中心变化（PCV）。
如何修正天线相位中心偏差呢？
对于卫星或者接收机天线相位偏差修正，我们可以通过IGS发布的atx文件。
一般只有在精密单点定位中我们需要考虑卫星和接收机的天线相位中心修正。
在RTK中，一般可以不修正天线相位中心变化。
10.相对论效应
11.潮汐改正：主要分成了三部分：地球固体潮、海洋负荷潮、极潮。在精密单点定位中应使用相应的模型进行改正。
12.固体潮
是指摄动天体(月球、太阳)对弹性地球的引力作用，引起地球表面周期性涨落的现象。
固体地球潮汐引起的测站周期性位移与测站所处的纬度有关，在高程方向可达30cm、在水平方向可达5cm。
固体地球潮则能通过相对简单的地球模型精确计算出来。
13.海洋负荷
是指在海潮期间由于海水质量重新分布所引起的海床和海岸形变。在海水重量作用下，地壳会发生弹性形变，称为海洋负荷潮。
海潮改正比固体潮小一个量级，对精密单点定位单历元解(单历元解：一个历元下的定位解；那每个历元都会求解，每个历元的解都会有该影响)的影响可达5cm，单天静态定位结果的影响为mm级。当测站与海岸线的距离大于1000km时，海潮的影响可忽略不计。
与固体潮影响一样，在精密单点定位中，海潮的影响必须利用模型改正。
14.极潮
地球的自转轴会在20平方米的范围内漂移(极移)，引起地壳的弹性响应，从而导致地球表面测站位置发生变化，这一现象称为极潮。
极潮影响在垂向可达2.5cm，在水平方向上变形可达0.7cm，因而在高精度数据处理中应进行模型改正。
采用IERS提供的极潮改正模型，在输入测站经纬度后可以计算得到极潮改正值。
15.天线相位缠绕
相位缠绕（Phase Wind-Up）是发射端与接收端之间的相对运动导致的载波相位变化。对GPS系统来说，因为GPS卫星发送的是右旋圆极化（RHCP:Right Hand Circularly Polarized）的信号，在这种情况下，接收机或者卫星天线的旋转会导致载波相位发生改变，这个值可能达到一个载波周期，我们把这种现象叫做相位缠绕。
接收机端由于载体/接收机的运动导致的旋转/相位缠绕被接收机钟差吸收掉；因此，在PPP中不予以考虑，只考虑卫星端的相位缠绕。
所幸相位缠绕只影响载波相位测量，不影响码相位测量，在非精密定位中可以忽略其影响。
对差分定位来说其影响一般也可以忽略，尤其是短基线的时候。
然而对精密单点定位来说，其影响就不能忽略了，因其影响可能会达到分米级。
16.多路径效应
在GPS测量中，经测站周围各种介质如地表、建筑物等一次或多次反射的卫星信号，如果进入接收机天线，将与直接来自卫星的信号产生干涉，从而使观测值偏离真值，产生的误差称为多路径误差。
如何削弱多路径误差的影响：(多路径效应引起的误差无法完全消除，只能削弱)
- 选择合适的站址，天线安置尽量避开强反射物（如水面、山坡、高层建筑物等）
- 选择合适的GPS接收机及天线，选用防多路径效应的天线（如扼流圈天线等）
- 适当延⻓观测时间
17.电离层误差
在太阳紫外线、X射线、
射线和高能粒子等的作用下，电离层中的中性气体分子被电离，产生大量的电子和正离子，从而形成了一个电离区域，高度在60~1000km。
GNSS信号是以电磁波的形式进行传播的。
当电磁波穿过充满电子的电离层时，它的传播速度和方向会发生改变，由此造成GNSS测量中的电离层延时误差。
电离层是一种弥散性介质，即不同频率的电磁波在电离层中有着不同的传播速度。
电离层延时 I 与信号频率 f 之间的具体关系可表达如下：
由上式可见，伪距测量值中的电离层延迟与载波相位测量值中的电离层延迟大小相同，符号相反，两者相加和为0，这也是为什么可以进行无电离层组合观测值。
电离层延时 的大小一般为几米左右，但当太阳黑子活动增强时，电离层中的电子密度会升高，这使得电离层延时也随之增加，其值可达十几米，甚至几十米，因而GNSS通常不能忽略电离层延时对GNSS测量和定位的影响。事实上，电离层延时是GNSS测量中的最大误差量之一。
18.电离层经验改正模型
表述电离层中的电子密度、离子密度、电子温度、离子温度、离子成分和总电子含量等参数的时空变化规律的一些数学公式称为电离层模型。
常用的计算总电子含量的模型有本特(Bent)模型、国际参考电离层（IRI）模型、Klobuchar模型（克罗布歇模型）、GIM模型等。
Bent和IRI模型根据全球各电离层观测站⻓期积累的大量观测资料拟合出来的模型和经验公式,被电离层研究和无线电通信领域的用戶广泛使用。但模型相对复杂，一些参数难以获得，所以卫星导航用戶一般不使用此类模型。
19.Klobuchar(克罗布歇)模型
GPS导航电文中播发该模型的参数供单频用戶改正电离层，该模型将晚间的电离层时延视为常数，取值为5ns；把白天的时延看成是余弦函数中正的部分。
可将电离层延迟影响改正60%(使用该模型可以把电离层延迟的影响改正60%，即还剩40%)，为GPS单频用戶所广泛采用。
我国的北斗2代系统也播发了Klobuchar模型参数，在中国境内，其电离层延迟修正精度可在70%以上。
20.GIM模型
IGS发布事后的电离层产品，并以IONEX格式存储，可从各IGS数据中心下载。可将电离层延迟影响改正80%以上。
产品以 i 作为后缀。
21.电离层双频组合模型(使用两个频率的伪距和载波构建无电离层组合观测值)
从电离层误差的计算公式，卫星信号所受到的电离层延迟是与信号频率的平方成反比的。如果卫星能同时用两种频率来发射信号，那么这两种不同频率的信号就将沿着同一路径传播到达接收机。GNSS卫星之所以要用两种不同的频率来发射信号，其主要目的也在于此(在于哪？)。
这也是为什么GNSS卫星使用两种不同的频率来发射信号，用于构建伪距和载波的无电离层组合观测值，消除电离层延迟的一阶影响。
经典公式、经典系数，要牢牢记住。
22.对流层误差及其改正
对流层定义为高度在50km以下(在距离超过50km的高空中，对流层延迟的影响很小或者几乎没有)未被电离的中性大气层。与电离层不同，对频率30GHz以下的电磁波信号，对流层基本上是非色散介质，即信号折射与信号频率无关。
无法用双频改正的方法来消除对流层延迟，只能通过求出信号传播路径上各处的大气折射系数，然后进行积分来计算对流层延迟改正。在天顶方向上的延迟量约为2m，并且随着站星视线天顶距的增加而增大。
对于卫星高度⻆仅有几度(接近地面)的卫星，GPS信号的电离层延迟可以达到数米。一般来讲，对流层延迟与温度、气压、湿度以及GPS天线的位置有关。
对流层一般分为干分量和湿分量：
- 一部分为遵循理想气体定律的干分量，在海平面位置，它所引起的天顶延迟约为2.4m。静力延迟分量可以由在接收机天线处测定的气压精确计算出来。
- 另一部分为变化复杂的湿分量，它所引起的天顶延迟约为0.4m。由于水汽时空变化的复杂性，这使得难以精确计算湿延迟分量(当作参数进行求解)。
常用的对流层经验模型有：Saastamoinen、Hopfield、Black模型等。
23.Saastamoinen模型
24.卫星天顶距怎么计算？
卫星天顶距是从地球观测点到卫星在天顶方向上的角度，范围从0°（卫星在天顶正上方）到90°（卫星在地平线上）。
卫星的天顶距 = 90度 - 卫星高度角