神经网络的学习(Neural Networks: Learning)

1.代价函数

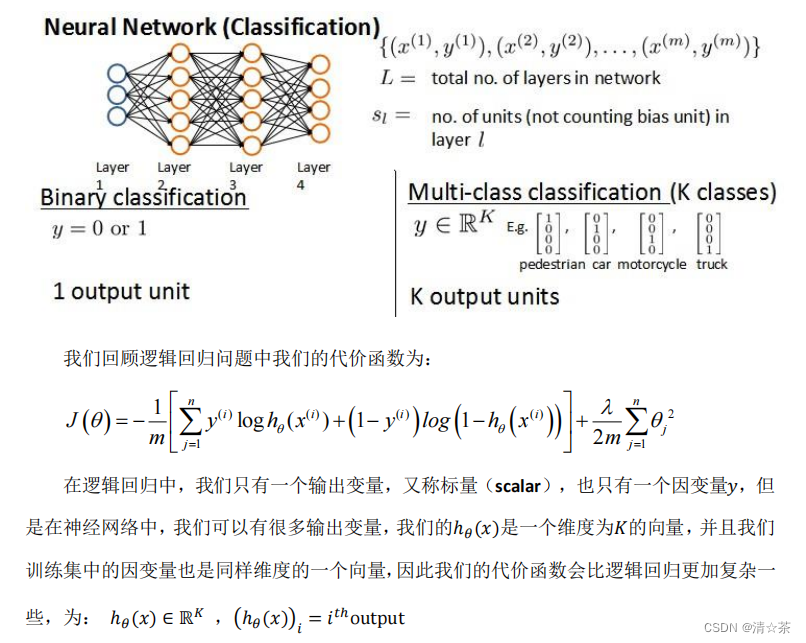
案例：假设神经网络的训练样本有个，每个包含一组输入和一组输出信号，表示神经网络层数，表示每层的 neuron 个数(表示输出层神经元个数)，代表最后一层中处理单元的个数。
将神经网络的分类定义为两种情况：二类分类和多类分类，
二类分类： = 0, = 0 1表示哪一类；
类分类： = , = 1表示分到第 i 类；( > 2)


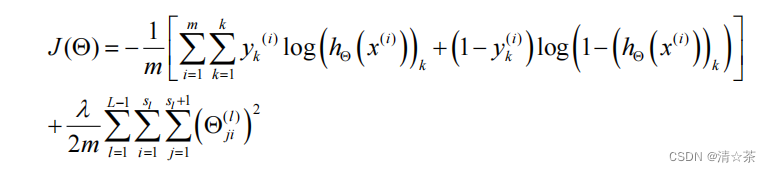
看起来复杂很多的代价函数背后的思想还是一样的，我们希望通过代价函数来观察算法预测的结果与真实情况的误差有多大，唯一不同的是，对于每一行特征，我们都会给出个预测，基本上我们可以利用循环，对每一行特征都预测个不同结果，然后在利用循环在个预测中选择可能性最高的一个，将其与中的实际数据进行比较。
正则化的那一项只是排除了每一层0后，每一层的 矩阵的和。最里层的循环循环所
有的行（由 +1 层的激活单元数决定），循环则循环所有的列，由该层（层）的激活单元数所决定。即：ℎ()与真实值之间的距离为每个样本-每个类输出的加和，对参数进行regularization 的 bias 项处理所有参数的平方和。

在机器学习中，代价函数（Cost Function）是用来衡量模型预测误差的函数。它通常用于训练模型，以最小化预测误差。

代价函数的定义取决于所使用的模型和算法。对于线性回归模型，代价函数通常是平方误差代价函数，即将预测值与实际值之间的差的平方和作为目标函数进行优化。对于逻辑回归模型，代价函数通常是对数损失函数，即对预测概率取对数后与实际标签进行比较。

在训练模型时，通过迭代更新模型参数，使得代价函数的值逐渐减小。常用的优化算法包括梯度下降、随机梯度下降、牛顿法等。

选择合适的代价函数是训练模型的关键步骤之一。不同的代价函数适用于不同的问题和数据类型。在实际应用中，需要根据具体问题和数据特征选择合适的代价函数和优化算法，以获得更好的模型预测性能。

2.反向传播算法

正向传播方法，我们从第一层开始正向一层一层进行计算，直到最后一层的ℎ(),从前往后。
反向传播算法，也就是首先计算最后一层的误差，然后再一层一层反向求出各层的误差，直到倒数第二层。
案例：


反向传播算法（Backpropagation Algorithm）是一种在神经网络中用于根据误差更新各层连接权重的算法。它是基于梯度下降法的一种学习算法，通过不断地迭代，使神经网络的预测结果不断逼近实际值，从而不断优化神经网络的参数。

反向传播算法的工作原理是，首先通过正向传播计算得到输出结果，然后根据这个结果和实际值的误差计算出误差，再将这个误差反向传播到每一层神经元，更新每一层神经元的权重，以减小误差。这个过程一直持续到模型收敛，即达到预设的误差阈值或者迭代次数。

反向传播算法的核心是梯度下降，即在每个迭代步骤中，根据当前参数的梯度方向更新参数，使参数朝着减小误差的方向进行优化。具体来说，梯度下降算法会计算代价函数的偏导数，然后根据这个偏导数来更新参数。

反向传播算法的优点包括：能够自适应地学习输入和输出之间的映射关系；能够处理大规模的数据；通过不断优化参数，提高模型的预测精度；能够处理非线性问题等。但是，反向传播算法也存在一些缺点，例如容易陷入局部最优解，训练时间较长等。因此，在实际应用中，需要根据具体问题和数据特征选择合适的神经网络结构和优化算法，以获得更好的模型预测性能。

3.反向传播算法的直观理解

前向传播算法：

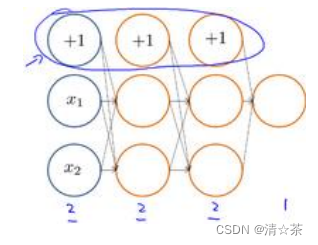
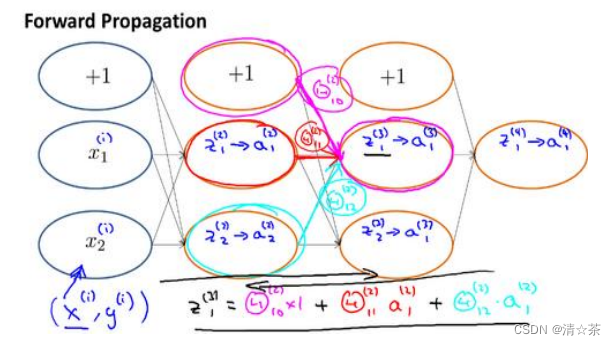
而反向传播算法的直观理解可以这样描述：

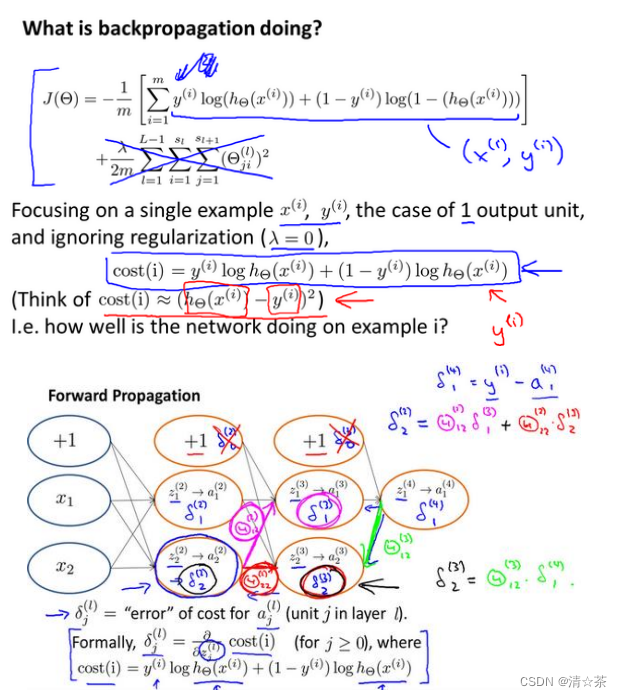
想象一个多层的大蛋糕，每一层都有一些糖霜（代表神经元的输出）和糖粒（代表神经元的输入）。我们想要调整糖粒的量，使得糖霜的总量（代表网络的输出）与我们想要的总量尽可能接近。

首先，我们计算出实际的糖霜总量与我们想要的糖霜总量之间的差距。这个差距就是我们的误差。

然后，我们开始从蛋糕的顶层（网络的输出层）开始，将每一层的糖粒调整一点，看看是否可以使误差变小。这个调整的过程就是反向传播。

我们会一直调整，直到误差达到我们能够接受的范围，或者直到我们没有更多的糖粒可以调整为止。

在神经网络的情境下，每一层的糖粒都对应一个神经元的权重。当我们想要调整一个糖粒时，我们实际上是在调整与这个糖粒相连的神经元的权重。通过不断地调整权重，我们希望最终能够得到一个满意的糖霜总量，也就是网络的输出。

以上就是反向传播算法的直观理解。这个算法允许我们通过局部的、微小的调整，逐步地优化网络的参数，以实现全局的最优解。

4.实现注意：展开参数

把参数从矩阵展开成向量，以便我们在高级最优化步骤中的使用需要。

5.梯度检验

梯度的数值检验（Numerical Gradient Checking）方法。这种方法的思想是通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。
对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的 ，我们计算出在 - 处和 + 的代价值（是一个非常小的值，通常选取 0.001），然后求两个代价的平均，用以估计在 处的代价值。


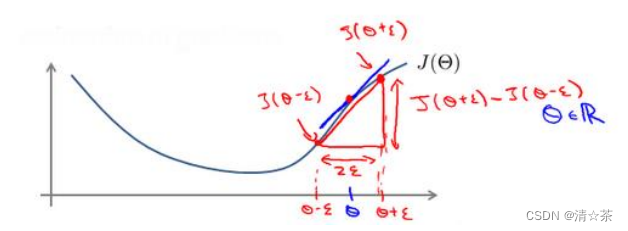
梯度检验是一种用于验证神经网络中反向传播算法是否正确的方法。它的基本思想是通过计算梯度值来检验之前计算的导数是否符合要求。

具体来说，梯度检验的方法是在曲线上取一点，对这点进行微小的扰动，然后计算出微扰后的两个点之间的斜率。通常，这个斜率是非常小的，因为我们在做微扰动。然后，我们可以使用这个斜率来估计在这一点上的梯度。

如果反向传播算法是正确的，那么这个梯度值应该与通过反向传播算法计算出的梯度值非常接近。如果两者相差很大，那么就说明反向传播算法在这一点上可能存在问题，需要进一步检查和修正。

梯度检验的优点是可以帮助我们发现反向传播算法中可能存在的错误，提高模型的精度和稳定性。但是，它也有一些缺点，比如计算量大，计算复杂度高，可能会增加模型的训练时间和成本等。因此，在实际应用中，我们需要根据具体问题和数据特征选择合适的梯度检验方法和参数设置，以获得更好的模型预测性能。

6.随机初始化

随机初始化是一种常见的权重初始化方法，用于神经网络的训练。在神经网络中，权重和偏置的初始值对模型的训练结果有很大影响。如果初始值设置不当，可能会导致模型收敛速度慢、陷入局部最优等问题。

随机初始化方法是将权重和偏置初始化为随机的值，通常是在一个小的随机范围内。这个随机范围的选择会影响到模型的训练效果。常见的随机初始化方法包括从均匀分布或高斯分布中随机采样。

随机初始化的优点包括：
可以打破对称性，为神经元提供不同的起点，促进网络的多样性和学习能力。
可以提高模型的泛化能力，因为不同的初始值会导致模型在不同的解空间中进行搜索，增加找到更好解的可能性。
但是，随机初始化也存在一些问题，如可能会带来训练不稳定、对称性和梯度消失或爆炸等问题。此外，如果初始化参数不当，可能会影响模型的训练速度和精度。因此，在选择随机初始化方法时，需要根据具体问题和数据特征选择合适的随机范围和分布，并进行相应的调整和优化。

7.综合总结（重要）

小结一下使用神经网络时的步骤：
网络结构：第一件要做的事是选择网络结构，即决定选择多少层以及决定每层分别有多少个单元。
第一层的单元数即我们训练集的特征数量。（输入值）
最后一层的单元数是我们训练集的结果的类的数量。（输出值）
如果隐藏层数大于 1，确保每个隐藏层的单元个数相同，通常情况下隐藏层单元的个数越多越好。
我们真正要决定的是隐藏层的层数和每个中间层的单元数。
训练神经网络：

1. 参数的随机初始化
2. 利用正向传播方法计算所有的ℎ()
3. 编写计算代价函数 的代码
4. 利用反向传播方法计算所有偏导数
5. 利用数值检验方法检验这些偏导数
6. 使用优化算法来最小化代价函数

8.自主驾驶

使用神经网络来实现自动驾驶，也就是说使汽车通过学习来自己驾驶。
案例：
在下面也就是左下方，就是汽车所看到的前方的路况图像。

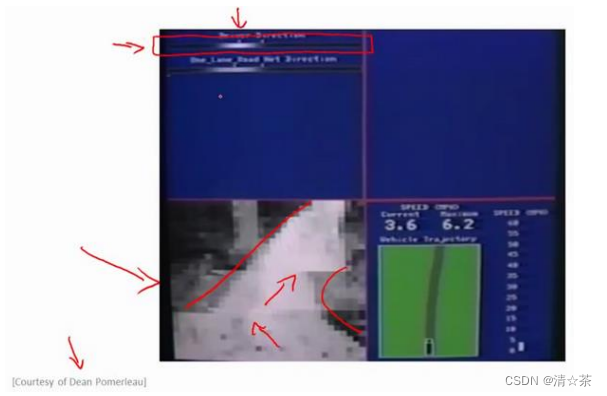
在图中你依稀能看出一条道路，朝左延伸了一点，又向右了一点，然后上面的这幅图，你可以看到一条水平的菜单栏显示的是驾驶操作人选择的方向。就是这里的这条白亮的区段显示的就是人类驾驶者选择的方向。比如：最左边的区段，对应的操作就是向左急转，而最右端则对应向右急转的操作。因此，稍微靠左的区段，也就是中心稍微向左一点的位置，则表示在这一点上人类驾驶者的操作是慢慢的向左拐。
这幅图的第二部分对应的就是学习算法选出的行驶方向。并且，类似的，这一条白亮的区段显示的就是神经网络在这里选择的行驶方向，是稍微的左转，并且实际上在神经网络开始学习之前，你会看到网络的输出是一条灰色的区段，就像这样的一条灰色区段覆盖着整个区域这些均称的灰色区域，显示出神经网络已经随机初始化了，并且初始化时，我们并不知道汽车如何行驶，或者说我们并不知道所选行驶方向。只有在学习算法运行了足够长的时间之后，才会有这条白色的区段出现在整条灰色区域之中。显示出一个具体的行驶方向这就表示神经网络算法，在这时候已经选出了一个明确的行驶方向，不像刚开始的时候，输出一段模糊的浅灰色区域，而是输出一条白亮的区段，表示已经选出了明确的行驶方向。

机器学习在自主驾驶领域中有着广泛的应用，下面介绍一些机器学习在自主驾驶中的案例：

感知和识别：机器学习算法可以用于感知和识别车辆周围的环境，包括道路标志、车辆、行人和其他障碍物等。例如，深度学习算法可以用于图像识别，通过训练大量的图像数据集来提高识别准确率。
决策规划和控制：机器学习算法可以用于自主驾驶中的决策规划和控制。例如，强化学习算法可以用于规划行驶轨迹和速度，以及控制车辆的油门、刹车和转向等。
路径规划和导航：机器学习算法可以用于路径规划和导航，例如使用Dijkstra算法或A*搜索算法等来寻找最优路径。同时，机器学习还可以用于地图构建和定位，例如使用卡尔曼滤波器或粒子滤波器等算法进行车辆定位和地图构建。
行为预测和模拟：机器学习算法可以用于预测和模拟驾驶行为。例如，使用机器学习算法对历史驾驶数据进行训练和学习，可以预测驾驶员的驾驶行为和决策，从而为自主驾驶提供参考和借鉴。
总之，机器学习在自主驾驶领域中的应用非常广泛，从感知和识别到决策规划和控制，再到路径规划和导航、行为预测和模拟等方面都有着重要的应用。随着机器学习技术的发展和完善，自主驾驶技术的安全性和可靠性也将得到进一步提升。