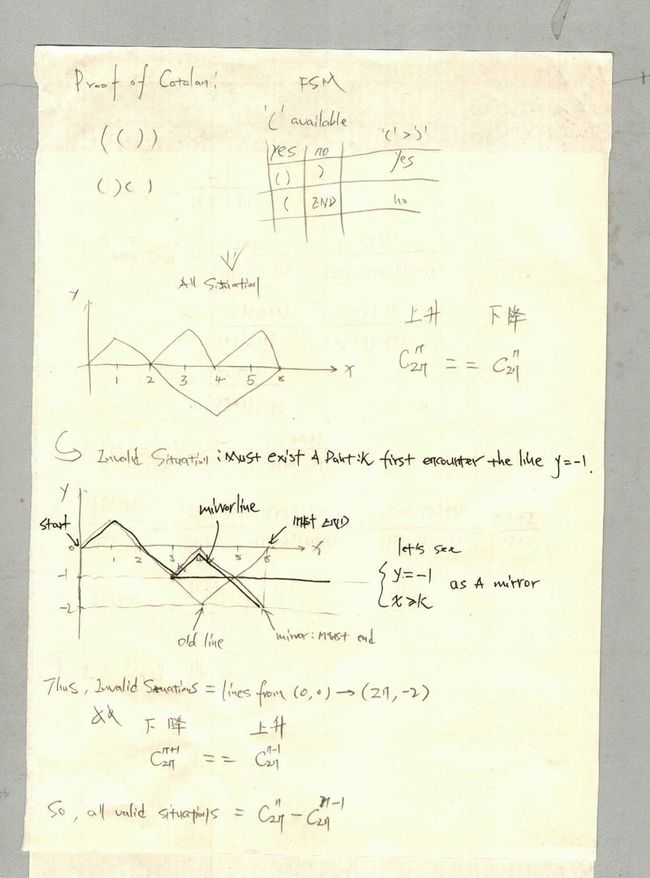
Proof of Catalan Number

Proof of Catalan Number：证明卡塔兰数列

 

In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involving recursively-defined objects. They are named after the Belgian mathematician Eugène Charles Catalan (1814–1894).

Here is a mathematical proof for the Catalan num.

 

  The Catalan sequence was described in the 18th century by Leonhard Euler, who was interested in the number of different ways of dividing a polygon into triangles.

  The sequence is named after Eugène Charles Catalan, who discovered the connection to parenthesized expressions during his exploration of the Towers of Hanoi puzzle. The counting trick for Dyck words was found by D. André in 1887.

  In 1988, it came to light that the Catalan number sequence had been used in China by the Mongolian mathematician Mingantu by 1730.That is when he started to write his book Ge Yuan Mi Lu Jie Fa, which was completed by his student Chen Jixin in 1774 but published sixty years later. P.J. Larcombe (1999) sketched some of the features of the work of Mingantu, including the stimulus of Pierre Jartoux, who brought three infinite series to China early in the 1700s.