刷题 ----- 动态规划
文章目录
- 1. 斐波那契数
- 2.阶数博弈
- 3.比特位计算
- 4. 传递信息
- 5.连续天数的最高销售额(最大数组和)
- 6.下载插件
- 7.反转数位
- 8. 三步问题
- 9.买股票的最佳时期
- 10. 按摩师(打家劫舍)
下面就是leetcode上所有关于动态规划的简单题了,有好多是重复的,也就没写。
设计出转移状态方程,以及初始化的值,是用动态规划解题的关键。
1. 斐波那契数

经典,我只能说经典,所有人一开始学习动态规划,就是这个斐波那契数列吧。
- 状态转移方程:dp[i] = dp[i - 1] + dp[i - 2];
- 设定初始值: dp[0] = 0 dp[1] = 1
int fib(int n)
{
int f[31] = {0};
f[0] = 0;
f[1] = 1;
int i;
for (i = 2; i <= n; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
2.阶数博弈
- 所以状态转移方程组为 dp[i] = dp[i - 2];
- 初始值 dp[1] = false;
bool divisorGame(int n)
{
if(n == 1)
{
return false;
}
bool* dp = (bool*)malloc(sizeof(bool) * (n + 1));
dp[1] = false;
dp[2] = true;
for (int i = 3; i <= n; i++)
{
dp[i] = dp[i - 2];
}
return dp[n];
}
3.比特位计算

就这个的状态转移方程组,想不到根本想不到,在这里放着,回看吧。
int* countBits(int n, int* returnSize)
{
int* dp = (int*)malloc(sizeof(int) * (n + 1));
dp[0] = 0;
for (int i = 1; i <= n; i++)
{
dp[i] = dp[i & (i - 1)] + 1;
}
*returnSize = n + 1;
return dp;
}
4. 传递信息

这道题在以前做过当时使用DFS算法做的,而现在用动态规划做一下。
题目的意思是在第 k 轮的时候,从 0 刚好传到 n - 1的位置的方案数有多少种。
- 知道题目的意思后,我们可以创建一个二维数组出来,dp[k][n-1]。
- 行表示第几轮,而列则分别对应,该轮能到达每个朋友的方案数。
- 看下图,就是你在第0轮的时候,东西只能在自己手上,其他的谁也到不了。
- 所以,除了你自己,其余的全是0.
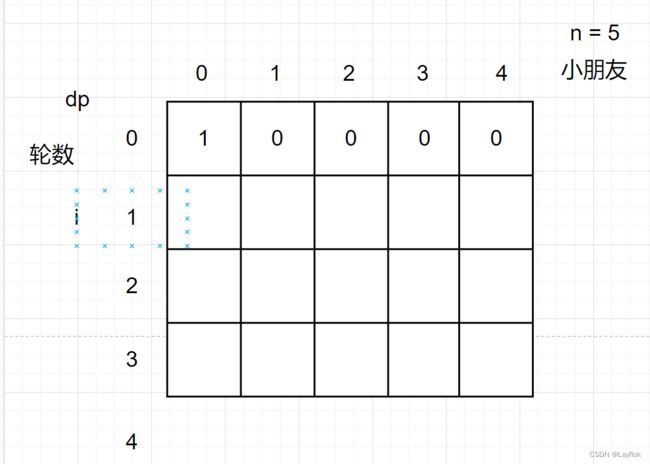
- 而第一轮就有变化了,就是新的一轮开始,去遍历所给 relation这个二维数组种记录是谁可以传递给谁。
- 你要判断当前这一轮能传递给谁,是不是取决于上一轮能传递给谁,如果上一轮都传递不到你那里,这一轮怎么又可能经过你传递呢?
- 所以看下图,第一轮需要去上一轮查找,在遍历relation数组的时候,往对应的dest位置去写方案数,要看上一轮的src是否有方案,有多少种方案。
- 因为上一轮只有0朋友有1种方案,所以其余的即使能传递,但也没办法。

再看下一轮。 - 因为上一轮只能到达 1 和 4 两个朋友手里,方案数都是1.
- 所以这一轮,能通过2 到达 0 1 3,全是1.
- 所以状态转移方程组: dp[i][dst] = dp[i-1][src];
- 初始化,dp[0][0] = 1.
int numWays(int n, int** relation, int relationSize, int* relationColSize, int k)
{
int** dp = (int**)malloc(sizeof(int*) * (k + 1));
int i,j;
for (i = 0; i <= k; i++)
{
dp[i] = (int*)malloc(sizeof(int) * n);
for (j = 0; j < n; j++)
{
dp[i][j] = 0;
}
}
dp[0][0] = 1;
for (i = 1; i <= k; i++)
{
for (j = 0; j < relationSize; j++)
{
//要想判断当前这一轮是否能到达某个点,得看上一轮你能到什么点。
int src = relation[j][0], dest = relation[j][1];
dp[i][dest] += dp[i-1][src];
}
}
return dp[k][n-1];
}
5.连续天数的最高销售额(最大数组和)

这俩是一道题,求出连续子数组的和,使其最大。
我如果直接看那个最大子数组的和描述,我感觉做不来。
但是看另一个题目描述,就感觉还行。
-
如果要实现最高的销售额,其实就可以利用前缀和的思想,挨个往起加,这样就能算出每个阶段的营销量。
-
但是如果你前一个的销售额为 负的或者等于 0 了。就没有必要再进行算了。
-
可以将当前的直接移动下来,接着再计算,就是下面这层逻辑。

当有了这样的思路的话,再看下面的方程就好多了,选出前一个和与当前的和,与当前的值的最大值。 -
状态转移方程组为 dp[i] = Max(dp[i - 1] + salse[i], salse[i]);
-
初始化: dp[0] = salse[0];
int Max(int x, int y)
{
return x > y ? x : y;
}
int maxSales(int* sales, int salesSize)
{
int* dp = (int*)malloc(sizeof(int) * salesSize);
dp[0] = sales[0];
int i,max = dp[0];
for (i = 1; i < salesSize; i++)
{
dp[i] = Max(dp[i-1] + sales[i], sales[i]);
if(dp[i] > max)
{
max = dp[i];
}
}
return max;
}
6.下载插件

这道题的意思就是所在最少的时间内,下载完所有的插件。
因为1分钟可以翻一次倍,所以利用贪心的思想,无限翻倍,直到一分钟可以下载的次数大于等于总共下载的次数时候,即可停止,然后再花费一分钟下载,这样的方式肯定是最快的。
dp[i] = num. 第i分钟的时候可以下载num个插件
- 状态转移方程:dp[i] = dp[i] * 2;
- 初始化值: dp[1] = 2;
因为最开始是下载一个插件,花费一分钟翻倍后就变成2个插件。
int leastMinutes(int n)
{
if(n <= 2)
{
return n;
}
int* dp = (int*)malloc(sizeof(int) * n);
//第一分钟直接翻倍
dp[1] = 2;
for (int i = 2; i < n; i++)
{
dp[i] = dp[i - 1] * 2;
if(dp[i] >= n)
{
return i + 1;
}
}
return -1;
}
7.反转数位
- 得到了二进制数位后,开始遍历,然后拿一个flag记录0的位置
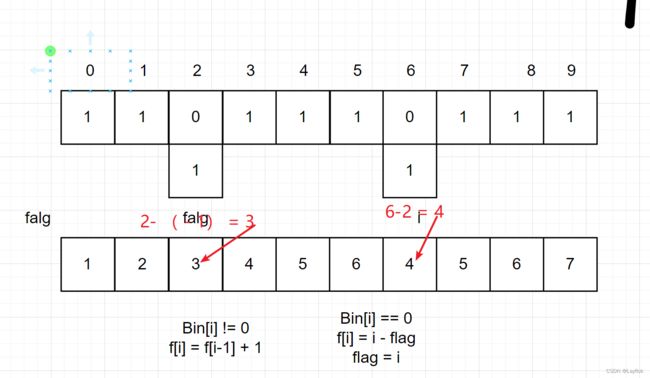
- 状态转移方程组 : dp[i] = dp[i - 1] + 1;
- 初始化 dp[0] = 1;
- 第一个永远是,因为你如果本来就是1那么长度就是1,如果你是0那么0也可以变成1.
int Max(int x, int y)
{
return x > y ? x : y;
}
void GetBin(int* bin,int size,int num)
{
int tmp = abs(num);
while(tmp != 0)
{
bin[size--] = tmp % 2;
tmp /= 2;
}
if(num < 0)
{
int i;
//按位取反
for (i = 1; i <= 32; i++)
{
if(bin[i] == 0)
{
bin[i] = 1;
}
else
{
bin[i] = 0;
}
}
//加1
i = 32;
while(i >= 0 && bin[i] == 1)
{
bin[i] = 0;
i--;
}
bin[i] = 1;
}
}
int reverseBits(int num)
{
if(num == -1)
{
return 32;
}
int* bin = (int*)malloc(sizeof(int) * 33);
memset(bin,0,sizeof(int) * 33);
int binSize = 32;
GetBin(bin,binSize,num);
int* dp = (int*)malloc(sizeof(int) * 33);
int flag = bin[0] == 0 ? 0 : -1; //0的下标
dp[0] = 1;
int i,maxLen = 1;
for (i = 1; i <= binSize; i++)
{
if(bin[i] != 0)
{
dp[i] = dp[i-1] + 1;
}
else
{
dp[i] = i - flag;
flag = i;
}
maxLen = Max(maxLen,dp[i]);
}
return maxLen;
}
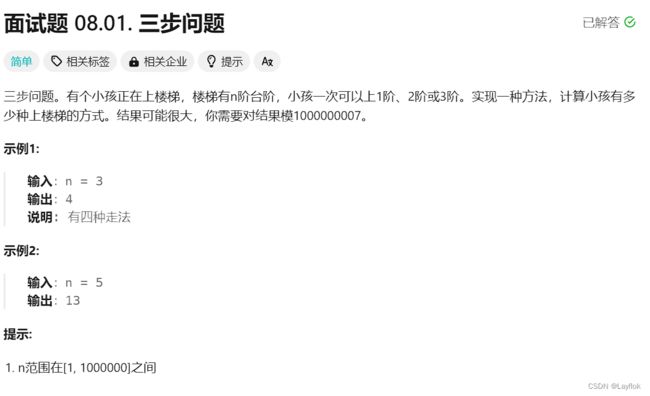
8. 三步问题
额。。爬楼梯?
typedef long long ll;
int waysToStep(int n)
{
ll* dp = (ll*)malloc(sizeof(ll) * (n + 5));
dp[0] = 1;
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i < (n + 5); i++)
{
dp[i] = (dp[i-1] + dp[i - 2] + dp[i - 3]) % 1000000007;
}
return dp[n];
}
9.买股票的最佳时期

这道题,咱也不是很清楚,自己的这种解法算不算动态规划额。。。。多了点分支语句。
我们在遍历prices数组的时候需要一直拿minPrice记录那个最底的价格,因为只有这样子,才会使利润最大化。
而当前的利润不就是: 价格减去当前最小的价格
- 状态转移方程组: dp[i] = price[i] - price[minPrice];
- 初始化值:dp[0] = 0,minPrics = 0;
- 取第一个就好,因为会随着比较而变化的。
int maxProfit(int* prices, int pricesSize)
{
int* dp = (int*)malloc(sizeof(int) * pricesSize);
int minPrice = 0;
dp[0] = 0;
int i,max = 0;
for (i = 1; i < pricesSize; i++)
{
if(prices[i] < prices[minPrice])
{
//更新一下最小值
minPrice = i;
dp[i] = 0;
}
else
{
dp[i] = prices[i] - prices[minPrice];
}
if(max < dp[i])
{
max = dp[i];
}
}
return max;
}
10. 按摩师(打家劫舍)

这道题的意思就是说从这个数组中,选出和最大的序列,但是每个数与每个数不能相邻。
如果只有两个数,那么我们选择最大的那个就好了。

如果有三个数,也就两种情况,选择第一家和三家,或者说是就选择第二家。

依次往后类推,中途如果发现和小于前一个,就说明你当前的方案不行,不如前一个的方案和多,所以从此以后改成前一种方案的选法,也就是选择前一种方案的和。

-
所以状态转移方程组是 dp[i] = Min(dp[i - 2] + nums[i] , dp[i-1]). -
初始化值: dp[0] = nums[0] dp[1] = Max(nums[0],nums[1]);
int Max(int x, int y)
{
return x > y ? x : y;
}
int massage(int* nums, int numsSize)
{
if(numsSize == 0) return 0;
if(numsSize == 1) return nums[0];
int* dp = (int*)malloc(sizeof(int) * (numsSize + 2));
dp[0] = nums[0];
dp[1] = Max(nums[0],nums[1]);
for (int i = 2; i < numsSize; i++)
{
dp[i] = Max(dp[i-2] + nums[i],dp[i-1]);
}
return dp[numsSize-1];
}