公开密钥加密之RSA算法【概念+计算+代码实现】
文章目录
文章目录
- 文章目录
- 前言
- 背景
- 一、RSA算法描述
-
- 1️⃣密钥计算方法
- 2️⃣加密方法
- 3️⃣解密方法
- 二、算法举例
-
- 1️⃣密钥计算
- 2️⃣加密运算
- 3️⃣加密运算
- 三、算法实现
-
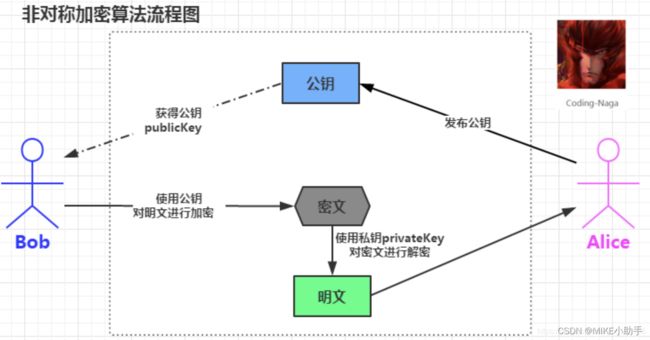
- 1️⃣RSA算法流程图
- 2️⃣代码实现
- 总结
推荐阅读:http://t.csdn.cn/nQfIY
前言
安全算法:公开密钥加密之RSA算法
公开密钥加密(又称“非对称加密”)是加密和解密使用不同密钥的一种加密方法。包括公开密钥和私有密钥(成对生成的,网上有工具网站)。
公开密钥(public key,后面简称P):加密用的密钥
私有密钥(secret key,后面简称S):解密用的密钥
背景
RSA公钥加密算法是1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。1987年首次公布,当时他们三人都在麻省理工学院工作。RSA就是他们三人姓氏开头字母拼在一起组成的。
RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的绝大多数密码攻击,已被ISO推荐为公钥数据加密标准。
今天只有短的RSA钥匙才可能被强力方式解破。到2008年为止,世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被解破的。但在分布式计算和量子计算机理论日趋成熟的今天,RSA加密安全性受到了挑战。
RSA算法基于一个十分简单的数论事实:将两个大质数相乘十分容易,但是想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。
RSA算法是现今使用最广泛的公钥密码算法,也是号称地球上最安全的加密算法。在了解RSA算法之前,先熟悉下几个术语
根据密钥的使用方法,可以将密码分为对称密码和公钥密码
对称密码:加密和解密使用同一种密钥的方式
公钥密码:加密和解密使用不同的密码的方式,因此公钥密码通常也称为非对称密码。
一、RSA算法描述
1️⃣密钥计算方法
1.选择两个大素数p和q(典型值为1024位)
2.计算n=p×q和z=(p-1)×(q-1)
// n表示欧拉函数
3.选择一个与z互质的数,令其为d
4.找到一个 e 使满足exd= 1 (mod z)
5.公开密钥为(e,m),私有密钥为(d,m)
2️⃣加密方法
1.将明文看成比特串,将明文划分成k位的块 P 即可,这里k是满足 2*k
加密
C = P e ( m o d n ) C = P^e (mod n) C=Pe(modn)
3️⃣解密方法
对每个密文块 C,计算 P=C^d(mod n),P即为明文
解密: P = c d ( m o d n ) P = c^d (mod n) P=cd(modn)
二、算法举例
1️⃣密钥计算
代码如下(示例):1.假设需要加密的明文信息为m=85,选择:e=7,p=11,q=13,说明使用RSA算法的加密和解密(计算密文并还原)
n=p*q=11*13=143
z=(p-1)*(q-1)=10*12=120
e*d=1(mod z)
7 * d( mod 120)=1 -------d=103
2️⃣加密运算
(示例):
公钥:(e,n)=(7,143)
密文c=p^e (mod n)=123
3️⃣加密运算
代码如下(示例):
密钥:(d,n)=(103,143)
明文:P=c^d (mod n)=85
三、算法实现
1️⃣RSA算法流程图
2️⃣代码实现
代码如下(示例):上题中的数据
编译软件:dev c++
#include总结
以上就是今天笔记,本文仅仅简单介绍了RSA 概念➕计算题➕代码实现