3_机械臂运动学之刚体的运动

机械臂为什么是6个自由度？

1.刚体力学

自由度：把确定一个力学体系在空间的几何位形所需要的独立变数的个数称为自由度.

刚体 ：刚体是这样一种质点组，组内任意两质点间的距离保持不变.

2.刚体的运动

2.1.1 刚体的自由度和运动的分类

1. 自由刚体的自由度

在三维空间中,含有 N 个质点的自由质点系的自由度为3N．但具有N个质点的刚体,其自由度却远远取不到这个值,因为这些质点彼此的距离必须保持不变,刚体的自由度应该是3N减去独立的关于相对位置的约束关系．但判断这些约束关系的独立性并非一目了然,于是我们不妨换一个思路分析刚体的自由度.由经验可知,要想确定一个刚体上所有质点的位置,只需知道其中任意三个不共线质点的位置就可以了．它们共有9个坐标,扣除彼此之间距离保持不变的三个约束关系,我们立即得到刚体的自由度是6.

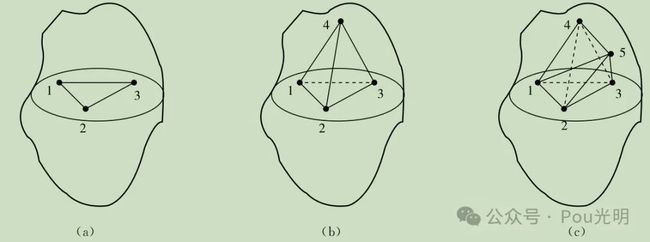
也可以这样来细致地理解这一问题．如图2.1.1(a)所示,先选取刚体内部任意三个不共线的质点,如上一段分析,这三个质点构成的小体系的自由度为6.然后再选取刚体内其他的任一质点加入该小体系,见图2.1.1(b)．新增的质点一方面增加了３个自由度,但同时也增加了３个独立的约束关系．这样净效应就是没有增加实际自由度,新的小体系自由度仍然是６．在图2.1.1(c)中,增加了第五个质点,尽管由此新添了该点到其他四个点距离为常数这四个约束关系,但只需其中的三个关系就能确定第五个质点的三个坐标分量,另一个约束关系不独立．这样自由度仍然为６．按此道理,逐点将刚体中的其他质点加入小体系,直至小体系扩大到成为整个刚体,自由度依然保持为６.

2、刚体运动的分类

如果除了上述刚性约束外,还有一些附加约束,则刚体自由度会进一步减小．

我们可以选择一些特别的附加约束,对刚体运动作如下分类．

(1)平动:当刚体运动时,其上的所有质点具有相同的速度和加速度,以其中一个质点的运动就可以表征整个刚体的运动,因而自由度是３;

(2)定轴转动:当刚体运动时,刚体上有两个质点保持位置不变,由于其余质点与这两个质点的距离要保持不变,可能的运动只能是以两个质点所在直线为轴,做自由度为１的转动;

(3)平面平行运动:当刚体运动时,刚体上任一点始终处于同一平面内,有两个平动自由度和一个转动自由度,总自由度为３;

(4)定点转动:当刚体运动时,刚体上有一点保持位置不变,增加了三个约束关系,因而自由度由一般情形的６减少为３;

(5)一般运动:刚体不受任何附加约束,自由度６．

2.1.2 刚体运动的欧拉定理

1. 惯性坐标系和本体坐标系

在研究刚体的运动时,需要用到两种坐标系．一种是普通的惯性坐标系,或称空间坐标系、固定坐标系,它是观察者所在的参考系．另一种固定在刚体上并与刚体同步运动,称为本体坐标系．

2. 刚体运动的欧拉定理

刚体运动的欧拉定理的表述是:具有一个固定点的刚体的任一位移,等效于绕该定点的某一轴线的转动．

证明 将本体坐标系和惯性坐标系的原点都取在该固定点上,则刚体绕固定点运动时,坐标系的原点不变,只是各个坐标轴随刚体的运动而改变方向,由线性代数知识,此时坐标系在做纯转动．于是,我们只要证明任一纯转动可等效为绕过原点的某轴线的转动,则欧拉定理得证．

证明过程略。

欧拉定理的一个直接的推论是沙勒定理,即刚体的一般运动是平动加转动．这是因为,刚体的一般运动可以视为刚体中某点的平动加上刚体相对于此点的运动．而根据欧拉定理,后一运动就是绕过该点的某转轴的转动．

“宏观世界空间为什么是三维的？”是一个有趣的问题．尽管物理学现在还不能很好地解释这个司空见惯的事实,但大自然偶尔会泄露这一维数与其他维数的不同之处．除了这里的例子,另外的例子还有电磁波在不同维度空间的传播特性不同．此外,不同维度空间中生物体的存在性与特性的分析也能从一个侧面来品味这一问题．

——《力学与理论力学》