【小呆的力学笔记】有限元专题之循环对称结构有限元原理

1. 循环对称问题的提出

许多工程结构都是其中某一扇面的n次周向重复，也就是是周期循环对称结构。如果弹性体的几何形状、约束情况以及所受的外部载荷都是对称于某一轴，则所有的应力、应变和位移也就对称于对称轴，那么这就是循环对称问题。典型的有发动机轮盘受离心力载荷下的应力分析，轮盘结构如下图1所示。观察轮盘结构，不难发现轮盘是扇形段重复多次的结构，那么离心力是周期循环对称的，并假设轮盘温度场是沿周向均布的，那么轮盘的应力应变应该也是周期循环对称的。

对于循环对称问题，事实上可以通过仅对某一扇面进行有限元模型就能获得正确的应力、应变和位移分析结果，当然需要在有限元算法中引入特殊的条件。

2. 循环对称条件

2.1 节点位移的循环对称关系

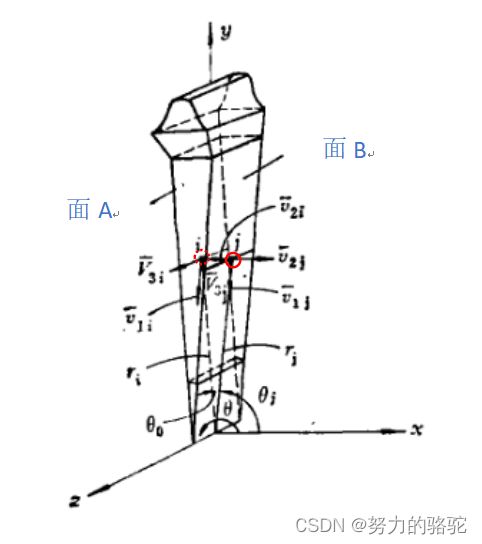
在循环对称问题中，需要引入柱坐标系，来给定循环对称条件。如下图，其中$xyz$是笛卡尔坐标系，$r\theta z$是柱坐标系，结构是典型轮盘的某一扇段。

在该循环对称问题中，扇面的面A的节点$i$和面B的对应节点$j$在柱坐标系$r\theta z$应该具有相同的坐标，同时应该也具备相同的位移变量。假设节点$i$和节点$j$分别属于面A和面B的一对对应节点，见下面示意图，那么其柱坐标下的位移变量应该满足下式关系：
$$\begin{gathered} u_{ri}=u_{rj} \\ {u}_{\theta i}=u_{\theta j} \\ {u}_{zi}=u_{zj} \end{gathered}$$

节点$i$在柱坐标系下的位移与在笛卡尔坐标系下的位移进行变换，具体的变换关系如下

$$\begin{gathered} -u_{ri}\sin \alpha -u_{\theta i}\cos \alpha =u_{xi} \\ {u}_{ri}\cos \alpha -u_{\theta i}\sin \alpha =u_{yi} \\ {u}_{zi}=u_{zi} \end{gathered}$$
写成矩阵形式
[ u x i u y i u z i ] = [ − sin ⁡ α − cos ⁡ α 0 cos ⁡ α − sin ⁡ α 0 0 0 1 ] [ u r i u θ i u z i ] \begin{bmatrix} u_{xi}\\u_{yi}\\u_{zi} \end{bmatrix}= \begin{bmatrix} -\sin\alpha & -\cos\alpha & 0\\ \cos\alpha &-\sin\alpha & 0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} u_{ri}\\u_{\theta i}\\u_{zi} \end{bmatrix} ​uxi​uyi​uzi​​ ​= ​−sinαcosα0​−cosα−sinα0​001​ ​ ​uri​uθi​uzi​​ ​
节点$j$在柱坐标系下的位移与在笛卡尔坐标系下的位移进行变换，具体的变换关系如下
$$\begin{gathered} u_{rj}\sin \beta -u_{\theta j}\cos \beta =u_{xj} \\ {u}_{rj}\cos \beta +u_{\theta j}\sin \beta =u_{yj} \\ {u}_{zj}=u_{zj} \end{gathered}$$
写成矩阵形式
[ u x j u y j u z j ] = [ sin ⁡ β − cos ⁡ β 0 cos ⁡ α sin ⁡ β 0 0 0 1 ] [ u r j u θ j u z j ] \begin{bmatrix}u_{xj}\\u_{yj}\\u_{zj}\end{bmatrix} =\begin{bmatrix} \sin\beta & -\cos\beta & 0\\ \cos\alpha &\sin\beta & 0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} u_{rj}\\u_{\theta j}\\u_{zj} \end{bmatrix} ​uxj​uyj​uzj​​ ​= ​sinβcosα0​−cosβsinβ0​001​ ​ ​urj​uθj​uzj​​ ​
那么
[ u r j u θ j u z j ] = [ sin ⁡ β cos ⁡ β 0 − cos ⁡ α sin ⁡ β 0 0 0 1 ] [ u x j u y j u z j ] \begin{bmatrix}u_{rj}\\u_{\theta j}\\u_{zj}\end{bmatrix} =\begin{bmatrix} \sin\beta & \cos\beta & 0\\ -\cos\alpha &\sin\beta & 0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} u_{xj}\\u_{yj}\\u_{zj} \end{bmatrix} ​urj​uθj​uzj​​ ​= ​sinβ−cosα0​cosβsinβ0​001​ ​ ​uxj​uyj​uzj​​ ​
由于
[ u r i u θ i u z i ] = [ u r j u θ j u z j ] \begin{bmatrix}u_{ri}\\u_{\theta i}\\u_{zi}\end{bmatrix} =\begin{bmatrix}u_{rj}\\u_{\theta j}\\u_{zj}\end{bmatrix} ​uri​uθi​uzi​​ ​= ​urj​uθj​uzj​​ ​
那么
[ u x i u y i u z i ] = [ − sin ⁡ α − cos ⁡ α 0 cos ⁡ α − sin ⁡ α 0 0 0 1 ] [ u r i u θ i u z i ] = [ − sin ⁡ α − cos ⁡ α 0 cos ⁡ α − sin ⁡ α 0 0 0 1 ] [ u r j u θ j u z j ] = [ − sin ⁡ α − cos ⁡ α 0 cos ⁡ α − sin ⁡ α 0 0 0 1 ] [ sin ⁡ β cos ⁡ β 0 − cos ⁡ α sin ⁡ β 0 0 0 1 ] [ u x j u y j u z j ] = [ − sin ⁡ α sin ⁡ β + cos ⁡ α cos ⁡ β − sin ⁡ α cos ⁡ β − cos ⁡ α sin ⁡ β 0 cos ⁡ α sin ⁡ β + sin ⁡ α cos ⁡ β cos ⁡ α cos ⁡ β − sin ⁡ α sin ⁡ β 0 0 0 1 ] [ u x j u y j u z j ] = [ cos ⁡ ( α + β ) − sin ⁡ ( α + β ) 0 sin ⁡ ( α + β ) cos ⁡ ( α + β ) 0 0 0 1 ] [ u x j u y j u z j ] = [ cos ⁡ ( θ ) − sin ⁡ ( θ ) 0 sin ⁡ ( θ ) cos ⁡ ( θ ) 0 0 0 1 ] [ u x j u y j u z j ] = [ θ 1 ] [ u x j u y j u z j ] \begin{bmatrix}u_{xi}\\u_{yi}\\u_{zi}\end{bmatrix} =\begin{bmatrix} -\sin\alpha & -\cos\alpha & 0\\ \cos\alpha &-\sin\alpha & 0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} u_{ri}\\u_{\theta i}\\u_{zi} \end{bmatrix} =\begin{bmatrix} -\sin\alpha & -\cos\alpha & 0\\ \cos\alpha &-\sin\alpha & 0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} u_{rj}\\u_{\theta j}\\u_{zj} \end{bmatrix}\\ =\begin{bmatrix} -\sin\alpha & -\cos\alpha & 0\\ \cos\alpha &-\sin\alpha & 0\\ 0&0&1 \end{bmatrix}\begin{bmatrix} \sin\beta & \cos\beta & 0\\ -\cos\alpha &\sin\beta & 0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} u_{xj}\\u_{yj}\\u_{zj} \end{bmatrix} \\ =\begin{bmatrix} -\sin\alpha\sin\beta+\cos\alpha\cos\beta & -\sin\alpha\cos\beta-\cos\alpha\sin\beta & 0\\ \cos\alpha\sin\beta+\sin\alpha\cos\beta & \cos\alpha\cos\beta-\sin\alpha\sin\beta &0\\ 0&0&1 \end{bmatrix}\begin{bmatrix} u_{xj}\\u_{yj}\\u_{zj} \end{bmatrix}\\ =\begin{bmatrix} \cos(\alpha+\beta) & -\sin(\alpha+\beta) & 0\\ \sin(\alpha+\beta) & \cos(\alpha+\beta) &0\\ 0&0&1 \end{bmatrix}\begin{bmatrix} u_{xj}\\u_{yj}\\u_{zj} \end{bmatrix}\\ =\begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0\\ \sin(\theta) & \cos(\theta) &0\\ 0&0&1 \end{bmatrix}\begin{bmatrix} u_{xj}\\u_{yj}\\u_{zj} \end{bmatrix}=\begin{bmatrix}\theta_1\end{bmatrix}\begin{bmatrix} u_{xj}\\u_{yj}\\u_{zj} \end{bmatrix} ​uxi​uyi​uzi​​ ​= ​−sinαcosα0​−cosα−sinα0​001​ ​ ​uri​uθi​uzi​​ ​= ​−sinαcosα0​−cosα−sinα0​001​ ​ ​urj​uθj​uzj​​ ​= ​−sinαcosα0​−cosα−sinα0​001​ ​ ​sinβ−cosα0​cosβsinβ0​001​ ​ ​uxj​uyj​uzj​​ ​= ​−sinαsinβ+cosαcosβcosαsinβ+sinαcosβ0​−sinαcosβ−cosαsinβcosαcosβ−sinαsinβ0​001​ ​ ​uxj​uyj​uzj​​ ​= ​cos(α+β)sin(α+β)0​−sin(α+β)cos(α+β)0​001​ ​ ​uxj​uyj​uzj​​ ​= ​cos(θ)sin(θ)0​−sin(θ)cos(θ)0​001​ ​ ​uxj​uyj​uzj​​ ​=[θ1​​] ​uxj​uyj​uzj​​ ​

2.2 节点内力的循环对称关系

扇形段I除了节点位移存在循环对称关系，剩余扇形对扇形段I的节点力也存在循环对称关系。典型的扇形段相互作用关系见下图，其中扇形段I是分析对象，扇形段II和扇形段III对扇形段I有相互作用。

其中扇形段I、II、III是重复扇形段，$i$、$i^{{}^{\prime }}$、$i^{{}^{\prime \prime }}$是一组对应周期循环节点，$j$、$j^{{}^{\prime }}$、$j^{{}^{\prime \prime }}$是一组对应周期循环节点。
其中$j^{{}^{\prime }}$对$i$的作用力为$f_{ri}$、$f_{\theta i}$、$f_{zi}$，$j$对$i^{{}^{\prime \prime }}$的作用力为$f_{r{i}^{{}^{\prime \prime }}}$、$f_{\theta i^{{}^{\prime \prime }}}$、$f_{z{i}^{{}^{\prime \prime }}}$，从周期循环对称特征定义，可知
$$\begin{gathered} f_{ri}=f_{r{i}^{{}^{\prime \prime }}} \\ {f}_{\theta i}=f_{\theta i^{{}^{\prime \prime }}} \\ {f}_{zi}=f_{z{i}^{{}^{\prime \prime }}} \end{gathered}$$
那么，$i^{{}^{\prime \prime }}$对$j$的作用力$f_{rj}$、$f_{\theta j}$、$f_{zj}$，存在如下关系式
$$\begin{gathered} f_{ri}=-f_{rj} \\ {f}_{\theta i}=-f_{\theta j} \\ {f}_{zi}=-f_{zj} \end{gathered}$$
注：上述节点力均在柱坐标系下。
参照上节节点位移的转换关系推导过程，不难推得在上述节点力关系式在笛卡尔坐标系下的表达式
[ f x i f y i f z i ] = − [ θ 1 ] [ f x j f y j f z j ] \begin{bmatrix}f_{xi}\\f_{yi}\\f_{zi}\end{bmatrix}=-\begin{bmatrix}\theta_1\end{bmatrix}\begin{bmatrix} f_{xj}\\f_{yj}\\f_{zj} \end{bmatrix} ​fxi​fyi​fzi​​ ​=−[θ1​​] ​fxj​fyj​fzj​​ ​

3. 在平衡方程中引入循环对称条件

若某循环结构包含一对循环对称节点$i$、$j$，不失一般性，平衡方程可以写成下式

[ k 11 k 12 ⋯ k 1 i ⋯ k 1 j ⋯ k 1 n k 21 k 22 ⋯ k 2 i ⋯ k 2 j ⋯ k 2 n ⋮ ⋮ ⋮ ⋮ ⋮ k i 1 k i 2 ⋯ k i i ⋯ k i j ⋯ k i n ⋮ ⋮ ⋮ ⋮ ⋮ k j 1 k j 2 ⋯ k j i ⋯ k j j ⋯ k j n ⋮ ⋮ ⋮ ⋮ ⋮ k n 1 k n 2 ⋯ k n i ⋯ k n j ⋯ k n n ] [ u 1 u 2 ⋮ u i ⋮ u j ⋮ u n ] = [ R 1 + F 1 F 2 ⋮ F i + f i ⋮ F j + f j ⋮ F n ] \begin{bmatrix}k_{11}&k_{12}&\cdots&k_{1i}&\cdots&k_{1j}&\cdots&k_{1n}\\ k_{21}&k_{22}&\cdots&k_{2i}&\cdots&k_{2j}&\cdots&k_{2n}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{i1}&k_{i2}&\cdots&k_{ii}&\cdots&k_{ij}&\cdots&k_{in}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{j1}&k_{j2}&\cdots&k_{ji}&\cdots&k_{jj}&\cdots&k_{jn}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{n1}&k_{n2}&\cdots&k_{ni}&\cdots&k_{nj}&\cdots&k_{nn}\\\end{bmatrix} \begin{bmatrix}u_1\\u_2\\\vdots\\u_i\\\vdots\\u_j\\\vdots\\u_n \end{bmatrix}=\begin{bmatrix}R_1+F_1\\F_2\\\vdots\\F_i+f_i\\\vdots\\F_j+f_j\\\vdots\\F_n \end{bmatrix} ​k11​k21​⋮ki1​⋮kj1​⋮kn1​​k12​k22​⋮ki2​⋮kj2​⋮kn2​​⋯⋯⋯⋯⋯​k1i​k2i​⋮kii​⋮kji​⋮kni​​⋯⋯⋯⋯⋯​k1j​k2j​⋮kij​⋮kjj​⋮knj​​⋯⋯⋯⋯⋯​k1n​k2n​⋮kin​⋮kjn​⋮knn​​ ​ ​u1​u2​⋮ui​⋮uj​⋮un​​ ​= ​R1​+F1​F2​⋮Fi​+fi​⋮Fj​+fj​⋮Fn​​ ​
式中$u_1$为模型的位移约束，有$u_1={\overline{u}}_1$，$R_1$为支反力；$F_i，i=1,\cdots$为节点外载荷，$f_i、f_j$为其他扇形段对扇形段I的作用力，这里引入循环对称条件，

$$\left[\begin{array}{c}{f}_i\end{array}\right]=-\left[\begin{array}{c}{\theta }_1\end{array}\right]\left[\begin{array}{c}{f}_j\end{array}\right]$$
上面平衡方程变成如下形式
[ k 11 k 12 ⋯ k 1 i ⋯ k 1 j ⋯ k 1 n k 21 k 22 ⋯ k 2 i ⋯ k 2 j ⋯ k 2 n ⋮ ⋮ ⋮ ⋮ ⋮ k i 1 k i 2 ⋯ k i i ⋯ k i j ⋯ k i n ⋮ ⋮ ⋮ ⋮ ⋮ k j 1 k j 2 ⋯ k j i ⋯ k j j ⋯ k j n ⋮ ⋮ ⋮ ⋮ ⋮ k n 1 k n 2 ⋯ k n i ⋯ k n j ⋯ k n n ] [ u ‾ 1 u 2 ⋮ u i ⋮ u j ⋮ u n ] = [ R 1 + F 1 F 2 ⋮ F i − θ f j ⋮ F j + f j ⋮ F n ] \begin{bmatrix}k_{11}&k_{12}&\cdots&k_{1i}&\cdots&k_{1j}&\cdots&k_{1n}\\ k_{21}&k_{22}&\cdots&k_{2i}&\cdots&k_{2j}&\cdots&k_{2n}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{i1}&k_{i2}&\cdots&k_{ii}&\cdots&k_{ij}&\cdots&k_{in}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{j1}&k_{j2}&\cdots&k_{ji}&\cdots&k_{jj}&\cdots&k_{jn}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{n1}&k_{n2}&\cdots&k_{ni}&\cdots&k_{nj}&\cdots&k_{nn}\\\end{bmatrix} \begin{bmatrix}\overline u_1\\u_2\\\vdots\\ u_i\\\vdots\\u_j\\\vdots\\u_n \end{bmatrix}=\begin{bmatrix}R_1+F_1\\F_2\\\vdots\\F_i-\theta f_j\\\vdots\\F_j+f_j\\\vdots\\F_n \end{bmatrix} ​k11​k21​⋮ki1​⋮kj1​⋮kn1​​k12​k22​⋮ki2​⋮kj2​⋮kn2​​⋯⋯⋯⋯⋯​k1i​k2i​⋮kii​⋮kji​⋮kni​​⋯⋯⋯⋯⋯​k1j​k2j​⋮kij​⋮kjj​⋮knj​​⋯⋯⋯⋯⋯​k1n​k2n​⋮kin​⋮kjn​⋮knn​​ ​ ​u1​u2​⋮ui​⋮uj​⋮un​​ ​= ​R1​+F1​F2​⋮Fi​−θfj​⋮Fj​+fj​⋮Fn​​ ​
进一步，用${\theta }^T$左乘第$i$行，则
[ k 11 k 12 ⋯ k 1 i ⋯ k 1 j ⋯ k 1 n k 21 k 22 ⋯ k 2 i ⋯ k 2 j ⋯ k 2 n ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 θ T k i 2 ⋯ θ T k i i ⋯ θ T k i j ⋯ θ T k i n ⋮ ⋮ ⋮ ⋮ ⋮ k j 1 k j 2 ⋯ k j i ⋯ k j j ⋯ k j n ⋮ ⋮ ⋮ ⋮ ⋮ k n 1 k n 2 ⋯ k n i ⋯ k n j ⋯ k n n ] [ u ‾ 1 u 2 ⋮ u i ⋮ u j ⋮ u n ] = [ R 1 + F 1 F 2 ⋮ θ T F i − f j ⋮ F j + f j ⋮ F n ] \begin{bmatrix}k_{11}&k_{12}&\cdots&k_{1i}&\cdots&k_{1j}&\cdots&k_{1n}\\ k_{21}&k_{22}&\cdots&k_{2i}&\cdots&k_{2j}&\cdots&k_{2n}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}&\theta^Tk_{i2}&\cdots&\theta^Tk_{ii}&\cdots&\theta^Tk_{ij}&\cdots&\theta^Tk_{in}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{j1}&k_{j2}&\cdots&k_{ji}&\cdots&k_{jj}&\cdots&k_{jn}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{n1}&k_{n2}&\cdots&k_{ni}&\cdots&k_{nj}&\cdots&k_{nn}\\\end{bmatrix} \begin{bmatrix}\overline u_1\\u_2\\\vdots\\ u_i\\\vdots\\u_j\\\vdots\\u_n \end{bmatrix}=\begin{bmatrix}R_1+F_1\\F_2\\\vdots\\\theta^TF_i-f_j\\\vdots\\F_j+f_j\\\vdots\\F_n \end{bmatrix} ​k11​k21​⋮θTki1​⋮kj1​⋮kn1​​k12​k22​⋮θTki2​⋮kj2​⋮kn2​​⋯⋯⋯⋯⋯​k1i​k2i​⋮θTkii​⋮kji​⋮kni​​⋯⋯⋯⋯⋯​k1j​k2j​⋮θTkij​⋮kjj​⋮knj​​⋯⋯⋯⋯⋯​k1n​k2n​⋮θTkin​⋮kjn​⋮knn​​ ​ ​u1​u2​⋮ui​⋮uj​⋮un​​ ​= ​R1​+F1​F2​⋮θTFi​−fj​⋮Fj​+fj​⋮Fn​​ ​
将第$i$行加到第$j$行，上式进一步变换为
[ k 11 k 12 ⋯ k 1 i ⋯ k 1 j ⋯ k 1 n k 21 k 22 ⋯ k 2 i ⋯ k 2 j ⋯ k 2 n ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 θ T k i 2 ⋯ θ T k i i ⋯ θ T k i j ⋯ θ T k i n ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 + k j 1 θ T k i 2 + k j 2 ⋯ θ T k i i + k j i ⋯ θ T k i j + k j j ⋯ θ T k i n + k j n ⋮ ⋮ ⋮ ⋮ ⋮ k n 1 k n 2 ⋯ k n i ⋯ k n j ⋯ k n n ] [ u ‾ 1 u 2 ⋮ u i ⋮ u j ⋮ u n ] = [ R 1 + F 1 F 2 ⋮ θ T F i − f j ⋮ F j + θ T F i ⋮ F n ] \begin{bmatrix}k_{11}&k_{12}&\cdots&k_{1i}&\cdots&k_{1j}&\cdots&k_{1n}\\ k_{21}&k_{22}&\cdots&k_{2i}&\cdots&k_{2j}&\cdots&k_{2n}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}&\theta^Tk_{i2}&\cdots&\theta^Tk_{ii}&\cdots&\theta^Tk_{ij}&\cdots&\theta^Tk_{in}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}+k_{j1}&\theta^Tk_{i2}+k_{j2}&\cdots&\theta^Tk_{ii}+k_{ji}&\cdots&\theta^Tk_{ij}+k_{jj}&\cdots&\theta^Tk_{in}+k_{jn}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{n1}&k_{n2}&\cdots&k_{ni}&\cdots&k_{nj}&\cdots&k_{nn}\\\end{bmatrix} \begin{bmatrix}\overline u_1\\u_2\\\vdots\\u_i\\\vdots\\u_j\\\vdots\\u_n \end{bmatrix}=\begin{bmatrix}R_1+F_1\\F_2\\\vdots\\\theta^TF_i-f_j\\\vdots\\F_j+\theta^TF_i\\\vdots\\F_n \end{bmatrix} ​k11​k21​⋮θTki1​⋮θTki1​+kj1​⋮kn1​​k12​k22​⋮θTki2​⋮θTki2​+kj2​⋮kn2​​⋯⋯⋯⋯⋯​k1i​k2i​⋮θTkii​⋮θTkii​+kji​⋮kni​​⋯⋯⋯⋯⋯​k1j​k2j​⋮θTkij​⋮θTkij​+kjj​⋮knj​​⋯⋯⋯⋯⋯​k1n​k2n​⋮θTkin​⋮θTkin​+kjn​⋮knn​​ ​ ​u1​u2​⋮ui​⋮uj​⋮un​​ ​= ​R1​+F1​F2​⋮θTFi​−fj​⋮Fj​+θTFi​⋮Fn​​ ​
将位移循环对称条件引入上式中
$$\left[\begin{array}{c}{u}_i\end{array}\right]=\left[\begin{array}{c}{\theta }_1\end{array}\right]\left[\begin{array}{c}{u}_j\end{array}\right]$$
那么平衡方程变换为
[ k 11 k 12 ⋯ k 1 i ⋯ k 1 j ⋯ k 1 n k 21 k 22 ⋯ k 2 i ⋯ k 2 j ⋯ k 2 n ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 θ T k i 2 ⋯ θ T k i i ⋯ θ T k i j ⋯ θ T k i n ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 + k j 1 θ T k i 2 + k j 2 ⋯ θ T k i i + k j i ⋯ θ T k i j + k j j ⋯ θ T k i n + k j n ⋮ ⋮ ⋮ ⋮ ⋮ k n 1 k n 2 ⋯ k n i ⋯ k n j ⋯ k n n ] [ u ‾ 1 u 2 ⋮ θ u j ⋮ u j ⋮ u n ] = [ R 1 + F 1 F 2 ⋮ θ T F i − f j ⋮ F j + θ T F i ⋮ F n ] \begin{bmatrix}k_{11}&k_{12}&\cdots&k_{1i}&\cdots&k_{1j}&\cdots&k_{1n}\\ k_{21}&k_{22}&\cdots&k_{2i}&\cdots&k_{2j}&\cdots&k_{2n}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}&\theta^Tk_{i2}&\cdots&\theta^Tk_{ii}&\cdots&\theta^Tk_{ij}&\cdots&\theta^Tk_{in}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}+k_{j1}&\theta^Tk_{i2}+k_{j2}&\cdots&\theta^Tk_{ii}+k_{ji}&\cdots&\theta^Tk_{ij}+k_{jj}&\cdots&\theta^Tk_{in}+k_{jn}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{n1}&k_{n2}&\cdots&k_{ni}&\cdots&k_{nj}&\cdots&k_{nn}\\\end{bmatrix} \begin{bmatrix}\overline u_1\\u_2\\\vdots\\\theta u_j\\\vdots\\u_j\\\vdots\\u_n \end{bmatrix}=\begin{bmatrix}R_1+F_1\\F_2\\\vdots\\\theta^TF_i-f_j\\\vdots\\F_j+\theta^TF_i\\\vdots\\F_n \end{bmatrix} ​k11​k21​⋮θTki1​⋮θTki1​+kj1​⋮kn1​​k12​k22​⋮θTki2​⋮θTki2​+kj2​⋮kn2​​⋯⋯⋯⋯⋯​k1i​k2i​⋮θTkii​⋮θTkii​+kji​⋮kni​​⋯⋯⋯⋯⋯​k1j​k2j​⋮θTkij​⋮θTkij​+kjj​⋮knj​​⋯⋯⋯⋯⋯​k1n​k2n​⋮θTkin​⋮θTkin​+kjn​⋮knn​​ ​ ​u1​u2​⋮θuj​⋮uj​⋮un​​ ​= ​R1​+F1​F2​⋮θTFi​−fj​⋮Fj​+θTFi​⋮Fn​​ ​
将$\theta$提出来，右乘到第$i$列，那么上式变为
[ k 11 k 12 ⋯ k 1 i θ ⋯ k 1 j ⋯ k 1 n k 21 k 22 ⋯ k 2 i θ ⋯ k 2 j ⋯ k 2 n ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 θ T k i 2 ⋯ θ T k i i θ ⋯ θ T k i j ⋯ θ T k i n ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 + k j 1 θ T k i 2 + k j 2 ⋯ θ T k i i θ + k j i θ ⋯ θ T k i j + k j j ⋯ θ T k i n + k j n ⋮ ⋮ ⋮ ⋮ ⋮ k n 1 k n 2 ⋯ k n i θ ⋯ k n j ⋯ k n n ] [ u ‾ 1 u 2 ⋮ u j ⋮ u j ⋮ u n ] = [ R 1 + F 1 F 2 ⋮ θ T F i − f j ⋮ F j + θ T F i ⋮ F n ] \begin{bmatrix}k_{11}&k_{12}&\cdots&k_{1i}\theta&\cdots&k_{1j}&\cdots&k_{1n}\\ k_{21}&k_{22}&\cdots&k_{2i}\theta&\cdots&k_{2j}&\cdots&k_{2n}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}&\theta^Tk_{i2}&\cdots&\theta^Tk_{ii}\theta&\cdots&\theta^Tk_{ij}&\cdots&\theta^Tk_{in}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}+k_{j1}&\theta^Tk_{i2}+k_{j2}&\cdots&\theta^Tk_{ii}\theta+k_{ji}\theta&\cdots&\theta^Tk_{ij}+k_{jj}&\cdots&\theta^Tk_{in}+k_{jn}\\ \vdots&\vdots& &\vdots& &\vdots& &\vdots\\ k_{n1}&k_{n2}&\cdots&k_{ni}\theta&\cdots&k_{nj}&\cdots&k_{nn}\\\end{bmatrix} \begin{bmatrix}\overline u_1\\u_2\\\vdots\\u_j\\\vdots\\u_j\\\vdots\\u_n \end{bmatrix}=\begin{bmatrix}R_1+F_1\\F_2\\\vdots\\\theta^TF_i-f_j\\\vdots\\F_j+\theta^TF_i\\\vdots\\F_n \end{bmatrix} ​k11​k21​⋮θTki1​⋮θTki1​+kj1​⋮kn1​​k12​k22​⋮θTki2​⋮θTki2​+kj2​⋮kn2​​⋯⋯⋯⋯⋯​k1i​θk2i​θ⋮θTkii​θ⋮θTkii​θ+kji​θ⋮kni​θ​⋯⋯⋯⋯⋯​k1j​k2j​⋮θTkij​⋮θTkij​+kjj​⋮knj​​⋯⋯⋯⋯⋯​k1n​k2n​⋮θTkin​⋮θTkin​+kjn​⋮knn​​ ​ ​u1​u2​⋮uj​⋮uj​⋮un​​ ​= ​R1​+F1​F2​⋮θTFi​−fj​⋮Fj​+θTFi​⋮Fn​​ ​

在上式中用缩减节点的位移列阵替换全节点位移列阵，即用$\left[\begin{array}{c}{\overline{u}}_1,u_2,\cdots ,u_{i-1},u_{i+1},\cdots ,u_j,\cdots ,u_n\end{array}\right]$替换$\left[\begin{array}{c}{\overline{u}}_1,u_2,\cdots ,u_{i-1},u_j，u_{i+1},\cdots ,u_j,\cdots ,u_n\end{array}\right]$
那么相应的要将位移列阵中第$i$行归属$u_j$合并到第$j$列，那么平衡方程变换为

[ k 11 k 12 ⋯ k 1 i − 1 k 1 i + 1 ⋯ k 1 i θ + k 1 j ⋯ k 1 n k 21 k 22 ⋯ k 2 i − 1 k 2 i + 1 ⋯ k 2 i θ + k 2 j ⋯ k 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 θ T k i 2 ⋯ θ T k i i − 1 θ T k i i + 1 ⋯ θ T k i i θ + θ T k i j ⋯ θ T k i n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 + k j 1 θ T k i 2 + k j 2 ⋯ θ T k i i − 1 + k j i − 1 θ T k i i + 1 + k j i + 1 ⋯ θ T k i i θ + k j i θ + θ T k i j + k j j ⋯ θ T k i n + k j n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ k n 1 k n 2 ⋯ k n i − 1 k n i + 1 ⋯ k n i θ + k n j ⋯ k n n ] n × ( n − 1 ) [ u ‾ 1 u 2 ⋮ u i − 1 u i + 1 ⋮ u j ⋮ u n ] ( n − 1 ) × 1 = [ R 1 + F 1 F 2 ⋮ θ T F i − f j ⋮ F j + θ T F i ⋮ F n ] \begin{bmatrix}k_{11}&k_{12}&\cdots&k_{1i-1}&k_{1i+1}&\cdots&k_{1i}\theta +k_{1j}&\cdots&k_{1n}\\ k_{21}&k_{22}&\cdots&k_{2i-1}&k_{2i+1}&\cdots&k_{2i}\theta+k_{2j}&\cdots&k_{2n}\\ \vdots&\vdots& &\vdots&\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}&\theta^Tk_{i2}&\cdots&\theta^Tk_{ii-1}&\theta^Tk_{ii+1} &\cdots&\theta^Tk_{ii}\theta+\theta^Tk_{ij}&\cdots&\theta^Tk_{in}\\ \vdots&\vdots& &\vdots&\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}+k_{j1}&\theta^Tk_{i2}+k_{j2}&\cdots&\theta^Tk_{ii-1}+k_{ji-1}&\theta^Tk_{ii+1} +k_{ji+1}&\cdots&\theta^Tk_{ii}\theta+k_{ji}\theta+\theta^Tk_{ij}+k_{jj}&\cdots&\theta^Tk_{in}+k_{jn}\\ \vdots&\vdots& &\vdots&\vdots& &\vdots& &\vdots\\ k_{n1}&k_{n2}&\cdots&k_{ni-1}&k_{ni+1}&\cdots&k_{ni}\theta+k_{nj}&\cdots&k_{nn}\\\end{bmatrix}_{n\times (n-1)} \begin{bmatrix}\overline u_1\\u_2\\\vdots\\u_{i-1}\\u_{i+1}\\\vdots\\u_j\\\vdots\\u_n \end{bmatrix}_{(n-1)\times 1}=\begin{bmatrix}R_1+F_1\\F_2\\\vdots\\\theta^TF_i-f_j\\\vdots\\F_j+\theta^TF_i\\\vdots\\F_n \end{bmatrix} ​k11​k21​⋮θTki1​⋮θTki1​+kj1​⋮kn1​​k12​k22​⋮θTki2​⋮θTki2​+kj2​⋮kn2​​⋯⋯⋯⋯⋯​k1i−1​k2i−1​⋮θTkii−1​⋮θTkii−1​+kji−1​⋮kni−1​​k1i+1​k2i+1​⋮θTkii+1​⋮θTkii+1​+kji+1​⋮kni+1​​⋯⋯⋯⋯⋯​k1i​θ+k1j​k2i​θ+k2j​⋮θTkii​θ+θTkij​⋮θTkii​θ+kji​θ+θTkij​+kjj​⋮kni​θ+knj​​⋯⋯⋯⋯⋯​k1n​k2n​⋮θTkin​⋮θTkin​+kjn​⋮knn​​ ​n×(n−1)​ ​u1​u2​⋮ui−1​ui+1​⋮uj​⋮un​​ ​(n−1)×1​= ​R1​+F1​F2​⋮θTFi​−fj​⋮Fj​+θTFi​⋮Fn​​ ​
事实上如果位移列阵自由度为$(n-1)$，那么相应的方程也只需要$(n-1)$个，因此我们去掉第$i$方程，那么平衡方程变成
[ k 11 k 12 ⋯ k 1 , i − 1 k 1 , i + 1 ⋯ k 1 i θ + k 1 j ⋯ k 1 n k 21 k 22 ⋯ k 2 , i − 1 k 2 , i + 1 ⋯ k 2 i θ + k 2 j ⋯ k 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ k i − 1 , 1 k i − 1 , 2 ⋯ k i − 1 , i − 1 k i − 1 , i + 1 ⋯ k i − 1 , i θ + k i − 1 , j ⋯ k i − 1 , n k i + 1 , 1 k i + 1 , 2 ⋯ k i + 1 , i − 1 k i + 1 , i + 1 ⋯ k i + 1 , i θ + k i + 1 , j ⋯ k i + 1 , n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ θ T k i 1 + k j 1 θ T k i 2 + k j 2 ⋯ θ T k i , i − 1 + k j , i − 1 θ T k i , i + 1 + k j , i + 1 ⋯ θ T k i i θ + k j i θ + θ T k i j + k j j ⋯ θ T k i n + k j n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ k n 1 k n 2 ⋯ k n i − 1 k n i + 1 ⋯ k n i θ + k n j ⋯ k n n ] ( n − 1 ) × ( n − 1 ) [ u ‾ 1 u 2 ⋮ u i − 1 u i + 1 ⋮ u j ⋮ u n ] ( n − 1 ) × 1 = [ R 1 + F 1 F 2 ⋮ F i − 1 F i + 1 ⋮ F j + θ T F i ⋮ F n ] \begin{bmatrix}k_{11}&k_{12}&\cdots&k_{1,i-1}&k_{1,i+1}&\cdots&k_{1i}\theta +k_{1j}&\cdots&k_{1n}\\ k_{21}&k_{22}&\cdots&k_{2,i-1}&k_{2,i+1}&\cdots&k_{2i}\theta+k_{2j}&\cdots&k_{2n}\\ \vdots&\vdots& &\vdots&\vdots& &\vdots& &\vdots\\ k_{i-1,1}&k_{i-1,2}&\cdots&k_{i-1,i-1}&k_{i-1,i+1} &\cdots &k_{i-1,i}\theta +k_{i-1,j}&\cdots&k_{i-1,n}\\ k_{i+1,1}&k_{i+1,2}&\cdots&k_{i+1,i-1}&k_{i+1,i+1} &\cdots &k_{i+1,i}\theta +k_{i+1,j}&\cdots&k_{i+1,n}\\ \vdots&\vdots& &\vdots&\vdots& &\vdots& &\vdots\\ \theta^Tk_{i1}+k_{j1}&\theta^Tk_{i2}+k_{j2}&\cdots&\theta^Tk_{i,i-1}+k_{j,i-1}&\theta^Tk_{i,i+1} +k_{j,i+1}&\cdots&\theta^Tk_{ii}\theta+k_{ji}\theta+\theta^Tk_{ij}+k_{jj}&\cdots&\theta^Tk_{in}+k_{jn}\\ \vdots&\vdots& &\vdots&\vdots& &\vdots& &\vdots\\ k_{n1}&k_{n2}&\cdots&k_{ni-1}&k_{ni+1}&\cdots&k_{ni}\theta+k_{nj}&\cdots&k_{nn}\\\end{bmatrix}_{(n-1)\times (n-1)} \begin{bmatrix}\overline u_1\\u_2\\\vdots\\u_{i-1}\\u_{i+1}\\\vdots\\u_j\\\vdots\\u_n \end{bmatrix}_{(n-1)\times 1}=\begin{bmatrix}R_1+F_1\\F_2\\\vdots\\F_{i-1}\\F_{i+1}\\\vdots\\F_j+\theta^TF_i\\\vdots\\F_n \end{bmatrix} ​k11​k21​⋮ki−1,1​ki+1,1​⋮θTki1​+kj1​⋮kn1​​k12​k22​⋮ki−1,2​ki+1,2​⋮θTki2​+kj2​⋮kn2​​⋯⋯⋯⋯⋯⋯​k1,i−1​k2,i−1​⋮ki−1,i−1​ki+1,i−1​⋮θTki,i−1​+kj,i−1​⋮kni−1​​k1,i+1​k2,i+1​⋮ki−1,i+1​ki+1,i+1​⋮θTki,i+1​+kj,i+1​⋮kni+1​​⋯⋯⋯⋯⋯⋯​k1i​θ+k1j​k2i​θ+k2j​⋮ki−1,i​θ+ki−1,j​ki+1,i​θ+ki+1,j​⋮θTkii​θ+kji​θ+θTkij​+kjj​⋮kni​θ+knj​​⋯⋯⋯⋯⋯⋯​k1n​k2n​⋮ki−1,n​ki+1,n​⋮θTkin​+kjn​⋮knn​​ ​(n−1)×(n−1)​ ​u1​u2​⋮ui−1​ui+1​⋮uj​⋮un​​ ​(n−1)×1​= ​R1​+F1​F2​⋮Fi−1​Fi+1​⋮Fj​+θTFi​⋮Fn​​ ​
将上式写成分块矩阵形式
$$\left[\begin{array}{cc}{k}_{11}& K_{12}\\ K_{21}& K_{22}\end{array}\right]\left[\begin{array}{c}{\overline{u}}_1\\ U_2\end{array}\right]=\left[\begin{array}{c}{R}_1+F_1\\ \hat{F}\end{array}\right]$$
将其展开
$$k_{11}{\overline{u}}_1+K_{12}{U}_2=R_1+$$