Games101:作业3(管线分析、深度插值、libpng warning、双线性插值等)
目录
0.作业介绍:
1.0.0 管线分析:
1.1.0 main函数
1.2.0 draw函数
1.3.0 rasterizer_triangle函数
1.3.1 重心坐标 computeBarycentric2D
1.3.2 深度插值
2.0.0 着色模型介绍
2.1 normal着色模型
2.2 phong模型
2.3 texture模型
2.3.1 Segmentation fault
2.3.2 libpng warning:iCCP:known incorrect sRGB profile
2.4 bump和displacement模型
3.0 提高部分:双线性插值:
4.0 结语
参考链接
0.作业介绍:
如上图所示为本次作业需要完成的任务,在介绍我对于本次作业的心得体会之前,我想先主观的感叹一句,我真的觉得这次作业很难。虽然上课时理论的学习是可以接受并理解的,但实操问题真的很多,我感觉我本次的作业基本上是“临摹”出来的。理论与实践脱轨的一个关键原因,我认为是有很多变量、对象没有弄清,没有理解它们对应的物理意义,所以在编写代码有些无从下手,不知道怎么把公式“变现”,所以我决定很有必要先介绍一下整个代码的实现流程,其中部分流程其实是在前两个作业已经出现的,但因为当时代码相对好写,所以没有彻底弄清楚,哎~
1.0.0 管线分析:
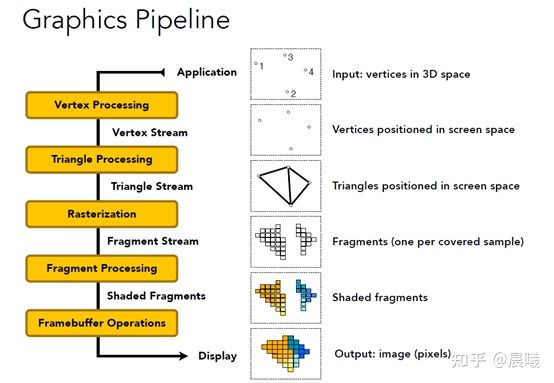
在Shading中,闫老师讲了图形管线的一系列操作[1],概括下来分别是[2]:
- Vertex Processing 点操作 :将三维空间上的点投影到二维
- Triangle Processing 三角形操作 :将三个点连成一个三角形/线,构造出一个平面/线,使得原三维空间物体变成由若干三角形组成的物体
- Raserization 光栅化:进行离散化的采样,用像素表示采样结果
- Fragment Processing 片元处理 :着色
- Framebuffer Operations片元缓冲操作:根据深度信息,确定遮挡和可视情况
下面我就按照管线的顺序,理一下整个流程,记录在注释里。
1.1.0 main函数
int main(int argc, const char** argv)
{
//记录组成三维图形的所有小三角形
std::vector TriangleList;
float angle = 140.0;
bool command_line = false;
std::string filename = "output.png";
objl::Loader Loader;
std::string obj_path = "./models/spot/";
// Load .obj File,加载模型
bool loadout = Loader.LoadFile("./models/spot/spot_triangulated_good.obj");
for(auto mesh:Loader.LoadedMeshes)
{
//对于图形中的每个面(即一个小三角形)的三个点记录在一起
for(int i=0;isetVertex(j,Vector4f(mesh.Vertices[i+j].Position.X,mesh.Vertices[i+j].Position.Y,mesh.Vertices[i+j].Position.Z,1.0));
t->setNormal(j,Vector3f(mesh.Vertices[i+j].Normal.X,mesh.Vertices[i+j].Normal.Y,mesh.Vertices[i+j].Normal.Z));
t->setTexCoord(j,Vector2f(mesh.Vertices[i+j].TextureCoordinate.X, mesh.Vertices[i+j].TextureCoordinate.Y));
}
//每三个顶点构成的一个小三角形放入TriangleList
TriangleList.push_back(t);
}
}
//初始化光栅化对象,定义屏幕长宽
rst::rasterizer r(700, 700);
//记录纹理到对象,注意rasterizer.hpp类有属性 optional texture
auto texture_path = "hmap.jpg";
r.set_texture(Texture(obj_path + texture_path));
//记录片元处理方式,类似于“赋值函数”,现默认方式是phong
std::function active_shader = phong_fragment_shader;
//处理传入的参数,注意在此处根据调用方式不同,修改了rasterizer对象的片元处理方式!
if (argc >= 2)
{
command_line = true;
filename = std::string(argv[1]);
if (argc == 3 && std::string(argv[2]) == "texture")
{
std::cout << "Rasterizing using the texture shader\n";
active_shader = texture_fragment_shader;
texture_path = "spot_texture.png";
r.set_texture(Texture(obj_path + texture_path));
}
else if (argc == 3 && std::string(argv[2]) == "normal")
{
std::cout << "Rasterizing using the normal shader\n";
active_shader = normal_fragment_shader;
}
else if (argc == 3 && std::string(argv[2]) == "phong")
{
std::cout << "Rasterizing using the phong shader\n";
active_shader = phong_fragment_shader;
}
else if (argc == 3 && std::string(argv[2]) == "bump")
{
std::cout << "Rasterizing using the bump shader\n";
active_shader = bump_fragment_shader;
}
else if (argc == 3 && std::string(argv[2]) == "displacement")
{
std::cout << "Rasterizing using the bump shader\n";
active_shader = displacement_fragment_shader;
}
}
//人眼所在位置
Eigen::Vector3f eye_pos = {0,0,10};
//设置顶点着色方式,获取顶点位置
r.set_vertex_shader(vertex_shader);
//设置片元着色方式,根据调用方式不同已赋值到active_shader
r.set_fragment_shader(active_shader);
int key = 0;//修改这个值,可以选择输出图片或动态旋转渲染的模型
int frame_count = 0;
if (command_line)
{
//清空两个缓冲区,在最后处理遮挡显示情况时发挥作用
r.clear(rst::Buffers::Color | rst::Buffers::Depth);
//分别设置MVP矩阵,用于对点操作,实现将三维的点映射到平面
r.set_model(get_model_matrix(angle));
r.set_view(get_view_matrix(eye_pos));
r.set_projection(get_projection_matrix(45.0, 1, 0.1, 50));
//光栅化、片元处理
r.draw(TriangleList);
cv::Mat image(700, 700, CV_32FC3, r.frame_buffer().data());
image.convertTo(image, CV_8UC3, 1.0f);
cv::cvtColor(image, image, cv::COLOR_RGB2BGR);
cv::imwrite(filename, image);
return 0;
}
while(key != 'q')
{
r.clear(rst::Buffers::Color | rst::Buffers::Depth);
r.set_model(get_model_matrix(angle));
r.set_view(get_view_matrix(eye_pos));
r.set_projection(get_projection_matrix(45.0, 1, 0.1, 50));
//r.draw(pos_id, ind_id, col_id, rst::Primitive::Triangle);
r.draw(TriangleList);
cv::Mat image(700, 700, CV_32FC3, r.frame_buffer().data());
image.convertTo(image, CV_8UC3, 1.0f);
cv::cvtColor(image, image, cv::COLOR_RGB2BGR);
cv::imshow("image", image);
cv::imwrite(filename, image);
key = cv::waitKey(0);
if (key == 'a' )
{
angle -= 0.1;
}
else if (key == 'd')
{
angle += 0.1;
}
}
return 0;
} 简而言之,主函数实现了:
①将顶点以三角形的方式每三个记录在一起,下图是Triangle类的一些属性,注意留意各个变量的名称和存储的内容,可以发现这一个类里装了三个顶点的顶点坐标、颜色、对应纹理坐标、法线。
②设置光栅化器的MVP模型(用于将三维的点变换到屏幕空间)
③根据调用命令的不同设置光栅化器的着色方式,之后便进入了rasterizer的draw函数。
1.2.0 draw函数
void rst::rasterizer::draw(std::vector &TriangleList) {
//zfar和znear之间的距离的一半
float f1 = (50 - 0.1) / 2.0;
//zfar个znear的中心z坐标
float f2 = (50 + 0.1) / 2.0;
//MVP变换矩阵
Eigen::Matrix4f mvp = projection * view * model;
//对每个小三角形进行操作,注意这个for循环一直到draw函数的结尾,
//故管线从此处开始其实是对每一个小三角形进行的(着色、深度处理等)
for (const auto& t:TriangleList)
{
Triangle newtri = *t;
//这里记录了只进行了MV变换的三角形的三个顶点,在本次作业中将此作为了视图空间viewspace
//的坐标,用于后续确定光源与物体表面的作用
//详见[3]https://games-cn.org/forums/topic/zuoye3-interpolated_shadingcoords/
std::array mm {
(view * model * t->v[0]),
(view * model * t->v[1]),
(view * model * t->v[2])
};
//记录viewspace的点坐标
std::array viewspace_pos;
std::transform(mm.begin(), mm.end(), viewspace_pos.begin(), [](auto& v) {
return v.template head<3>();
});
//经过MVP后的点坐标,投影到屏幕
Eigen::Vector4f v[] = {
mvp * t->v[0],
mvp * t->v[1],
mvp * t->v[2]
};
//x,y,z同除w,得到齐次坐标
//Homogeneous division
for (auto& vec : v) {
vec.x()/=vec.w();
vec.y()/=vec.w();
vec.z()/=vec.w();
}
//这里是为了计算仅进行了MV操作,即在viewspace下各顶点的法向量,具体解释见下文
Eigen::Matrix4f inv_trans = (view * model).inverse().transpose();
Eigen::Vector4f n[] = {
inv_trans * to_vec4(t->normal[0], 0.0f),
inv_trans * to_vec4(t->normal[1], 0.0f),
inv_trans * to_vec4(t->normal[2], 0.0f)
};
//视图变换,直接对X,Y,Z进行改变,而未使用变换矩阵,效果是相同的
//Viewport transformation
for (auto & vert : v)
{
vert.x() = 0.5*width*(vert.x()+1.0);
vert.y() = 0.5*height*(vert.y()+1.0);
vert.z() = vert.z() * f1 + f2;
}
//记录下经过MVP、齐次坐标变换和视图变换的顶点坐标
//完成顶点变换,变换到屏幕空间
for (int i = 0; i < 3; ++i)
{
//screen space coordinates
newtri.setVertex(i, v[i]);
}
//存储法向量n
for (int i = 0; i < 3; ++i)
{
//view space normal
newtri.setNormal(i, n[i].head<3>());
}
//设置颜色
newtri.setColor(0, 148,121.0,92.0);
newtri.setColor(1, 148,121.0,92.0);
newtri.setColor(2, 148,121.0,92.0);
//调用rasterizer_triangle,实现光栅化
//注意此时仍在循环中,故实际是对每个小三角形分别进行光栅化
//此时也传入了viewspace的顶点坐标,用于判断真实的光线作用
// Also pass view space vertice position
rasterize_triangle(newtri, viewspace_pos);
}
} 概括说,draw函数的作用在于对于每一个小三角形,分别计算了:
①仅进行MV操作、在viewspace空间中的顶点坐标,保存在mm,后传给了viewspace_pos,并传递到rasterizer_tirangle函数中,该坐标的作用在于后续计算光线作用,详见[3]:
②经过MVP变换的顶点坐标,保存在v,后进行了齐次坐标化,注意此时并未处理齐次坐标的w维,因为经过了MVP变换后,w坐标记录了原本的z值,这对于后续进行插值十分有用,等下文插值求深度时再展开说。
③viewspace下的顶点的法向量,保存在n,目的是在判断光线作用时,需要知道没有变形的三维物体的形状、位置信息,该法向量n和上方说的viewspace_pos皆是如此。
注意代码最初令newtri == *t,即利用newtri记录小三角形三个顶点的位置、法线、纹理、颜色,但后续修改了①位置,将其改成了经过MVP变换后的,②法线,将其改成了viewspace空间的。同时,viewspace的位置坐标虽然没有记录在newtri中,但是以参数的形式传递给了后续的rasterizer_triangle函数。
1.2.1 viewspace下的顶点的法向量
下面详细说一下viewspace下的顶点的法向量的计算过程,即下面这段代码的推导,此处参考了[4]:
Eigen::Matrix4f inv_trans = (view * model).inverse().transpose();
Eigen::Vector4f n[] = {
inv_trans * to_vec4(t->normal[0], 0.0f),
inv_trans * to_vec4(t->normal[1], 0.0f),
inv_trans * to_vec4(t->normal[2], 0.0f)
};首先提醒,我们需要计算的是viewspace下的法线,是仅进行了MV操作的,不是最初保存在t里的法向量,也不是进行了MVP变换的法向量。
假设,最初保存在三角形中的法向量为,切线为,经过MV操作后的法向量为,设MV变换矩阵为,则变换后切线为。现在需要计算的即为。因为Eigen中,代表矩阵乘法,需要满足前一个矩阵的列数等于后一个矩阵的行数,所以有以下公式:
令两式相等,再同乘的逆,再同乘的逆,即可得到:
又因为 M = view * modle,所以:
1.3.0 rasterizer_triangle函数
//Screen space rasterization
// 第一个参数:屏幕空间下的三角形,第二个参数:模型和视图变换后得到的三角形顶点,视图坐标下的坐标
void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array& view_pos)
{
// 将三维向量变为齐次坐标
auto v = t.toVector4();
// 光栅化,将三角形投影到屏幕空间,确定bounding box
// TODO: From your HW3, get the triangle rasterization code.
float minx = std::min(v[0][0],std::min(v[1][0],v[2][0]));
float miny = std::min(v[0][1],std::min(v[1][1],v[2][1]));
float maxx = std::max(v[0][0],std::max(v[1][0],v[2][0]));
float maxy = std::max(v[0][1],std::max(v[1][1],v[2][1]));
int min_x = floor(minx);
int min_y = floor(miny);
int max_x = round(maxx);
int max_y = round(maxy);
// TODO: Inside your rasterization loop:
// * v[i].w() is the vertex view space depth value z.
// * Z is interpolated view space depth for the current pixel
// * zp is depth between zNear and zFar, used for z-buffer
// 对于bounding box内的每一个像素进行判断,如果在三角形内,插值得到深度
// 根据深度判断遮挡情况,如果可以显示出来,则插值得到该像素的颜色、法线、纹理,
// 以及原本在viewspace下的坐标shadingcoords,用于判断光线情况
for(int i=min_x; i<=max_x; i++){
for(int j=min_y; j<=max_y; j++){
if(insideTriangle(i,j,t.v)){
//利用二维插值得到该点在屏幕三角形的α、β、γ值(重心坐标)
auto[alpha, beta, gamma] = computeBarycentric2D(i+0.5, j+0.5, t.v);
//修正得到viewspace中的情况
float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
zp *= Z;
//如果当前像素更靠前,则显示出来
if(zp < depth_buf[get_index(i,j)]){
depth_buf[get_index(i,j)] = zp;
//通过插值得到各个属性,color用于漫反射光照,
//normal用于确定色彩,texcoords用于确定纹理坐标,
//shadingcoords用于确定viewspace中点的位置,在光照中使用
auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1);
auto interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1);
auto interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1);
auto interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1);
//加载到模型中
fragment_shader_payload payload( interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
payload.view_pos = interpolated_shadingcoords;
// Use: Instead of passing the triangle's color directly to the frame
// buffer, pass the color to the shaders first to get the final color;
//根据模型,更新颜色,注意fragment_shader是在主函数中完成的“函数赋值”
//fragment_shader是根据命令不同而采取的不同shade方案
auto pixel_color = fragment_shader(payload);
set_pixel(Vector2i(i,j),pixel_color);
}
}
}
}
} 具体实现我已写在代码注释中,该函数的主要功能如下:
①光栅化,将三角形映射到屏幕的bounding-box
②采样判断每个像素是否在三角形中,如果在,则对其深度插值(computeBarycentric2D等,在1.3.1介绍),先得到屏幕空间的重心坐标,再修正得到view-space中的深度值,该部分参考了[4]、[5]、[6]、[7],在1.3.1和1.3.2介绍。
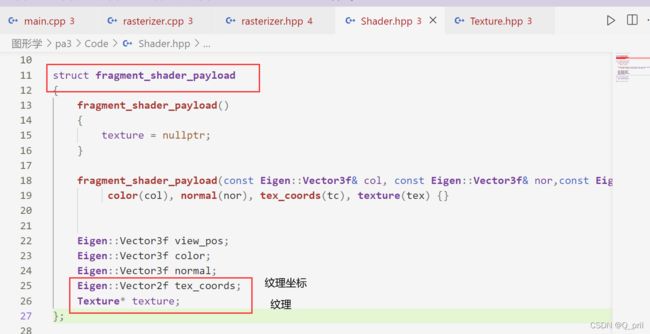
③通过插值得到三角形的各个属性,并用其初始化fragment_shader_payload结构的对象payload,注意fragment_shader_payload为Shader中定义的数据结构类型,payload为对象名,此对象用来记录当前像素的view_pos,颜色、法向量、纹理图中对应的坐标等。
而最后用来获取颜色的fragment_shader函数是先前在主函数通过“函数赋值”得到的着色函数,即下方的代码,根据命令不同fragment_shader意味着不同的着色方式(即主函数中的normal、phong、texture、bump等)。
//main.cpp
//模型中每个小三角形的顶点坐标
r.set_vertex_shader(vertex_shader);
//光栅化着色方式
r.set_fragment_shader(active_shader);
//rasterizer.cpp
void rst::rasterizer::set_vertex_shader(std::function vert_shader)
{
vertex_shader = vert_shader;
}
void rst::rasterizer::set_fragment_shader(std::function frag_shader)
{
fragment_shader = frag_shader;
} 1.3.1 重心坐标 computeBarycentric2D
这里解释一下computeBarycentric2D的原理,根据闫老师课堂所讲,可知可以通过一个点的重心坐标插值得到该点的各种属性,这里参考了[4]、[5]:
具体求解有行列式法和方程法,行列式是从重心坐标的定义出发利用三角形面积求解,方程法是根据重心坐标的性质(某一点的所有性质皆可以由三个顶点和α、β、γ得到)求解。
这里只介绍方程法,另外,最终算出的结果有多种表达方式(毕竟三角形面积有多种计算方式,用不同边则最后得到结果中含的未知数就不一样),这里只给出与代码中相同的表示:
根据重心坐标的性质可以列出一下式子:
将第一个式子代入后两个式子,消掉γ,可得:
消掉α,得:
同理即可得到α、γ,具体过程略,最终即为代码的形式:
static std::tuple computeBarycentric2D(float x, float y, const Vector4f* v){
float c1 = (x*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*y + v[1].x()*v[2].y() - v[2].x()*v[1].y()) / (v[0].x()*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*v[0].y() + v[1].x()*v[2].y() - v[2].x()*v[1].y());
float c2 = (x*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*y + v[2].x()*v[0].y() - v[0].x()*v[2].y()) / (v[1].x()*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*v[1].y() + v[2].x()*v[0].y() - v[0].x()*v[2].y());
float c3 = (x*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*y + v[0].x()*v[1].y() - v[1].x()*v[0].y()) / (v[2].x()*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*v[2].y() + v[0].x()*v[1].y() - v[1].x()*v[0].y());
return {c1,c2,c3};
} 1.3.2 深度插值
前面求出的α、β、γ其实是针对二维平面内三角形而言的,这个三角形是经过MVP和视图变换之后映射到屏幕的,此重心坐标与真实三维空间(因为MV仅涉及平移和等比例的缩放,没有使物体变形,所以这里所说的三维空间即为viewspace)中的重心坐标之间存在误差,所以代码后续有一个修正的操作,如下:
auto[alpha, beta, gamma] = computeBarycentric2D(i+0.5, j+0.5, t.v);
float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
zp *= Z;假设二维空间中小三角形三个顶点的深度值分别为,其内部一点的重心坐标为,对应深度值为;而三维空间三个顶点的深度值分别为,重心坐标为,对应深度值为,可得出下列公式,这里的原理参考了[4]、[6]、[7]。
①
⑤
联立①和⑤,可得:
⑥
⑦
⑧
可知⑥+⑦+⑧ = 1,将各式右边相加,提出Z,则得:
⑨
同理,对于任意属性,二维插值结果修复到三维的方式为:
⑩
auto[alpha, beta, gamma] = computeBarycentric2D(i+0.5, j+0.5, t.v);
float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
zp *= Z;再来看一下这个代码,Z得到的便是⑨式的结果,zp*=Z是⑩式代入属性Z的结果,这里提示一点,⑨中的是三维空间中的Z值,是否还记得draw函数中经过MVP变换后,齐次坐标下w的值即为Z的结果(因为投影矩阵最后一行为[ 0 0 1 0 ])。这里的代码其实是为了实现二维重心坐标修复到三维。但是其实在rasterizer_triangle的开头就使用了下图所示代码,即将t中的w值设置成了1,故代入可得:
(这里的α'等是代码中的α)
(Z是代码中的Z)
故zp实际还是二维插值得到的结果,并没有起到真正修正的效果,这里只是个近似,但是公式本身是有意义的!
// rasterizer_triangle函数
// 将三维向量变为齐次坐标
auto v = t.toVector4();
//Triangle.cpp
std::array Triangle::toVector4() const
{
std::array res;
std::transform(std::begin(v), std::end(v), res.begin(), [](auto& vec) { return Vector4f(vec.x(), vec.y(), vec.z(), 1.f); });
return res;
} 后续的interpolated_color、interpolated_normal、interpolated_texcoords、interpolated_shadingcoords同样是进行了一定的近似,根据老师给出的框架传入已计算传的重心坐标和需要插值的属性即可,当然自己写一个修复版的插值公式也是可以的。
2.0.0 着色模型介绍
下面,进入任务的主题,介绍一下各个着色模型同时记录一下我在写代码时的问题,这部分参考了[8]博主的代码。
2.1 normal着色模型
首先就是normal_fragment_shader:
Eigen::Vector3f normal_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f return_color = (payload.normal.head<3>().normalized() + Eigen::Vector3f(1.0f, 1.0f, 1.0f)) / 2.f;
Eigen::Vector3f result;
result << return_color.x() * 255, return_color.y() * 255, return_color.z() * 255;
return result;
}这里我说两点,首先是normal是法线的意思,虽然这个着色结果是各处地方颜色不同的小牛,但实际是由法线的变化形成的,并不涉及phong系统下的光照。
其次是第一行的代码,首先取出当前待着色像素点的法向量的X,Y,Z坐标并归一化,故此时X,Y,Z都在[-1,1]之间,加上(1.0f, 1.0f, 1.0f)后,变为[0,2],再除以2,即得[0,1],再分别乘以255即可得到各个颜色值了。
2.2 phong模型
Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
//不同光照模型的函数,注意漫反射取决于该点的color值
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
// light是一个数据类型,分别记录了灯光位置 和 强度
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector lights = {l1, l2};
//环境光强度
Eigen::Vector3f amb_light_intensity{10, 10, 10};
//人眼位置
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
//三维物体所在位置,即光线作用的点
Eigen::Vector3f point = payload.view_pos;
//三维物体的法线
Eigen::Vector3f normal = payload.normal;
//结果,是不同光累计的结果
Eigen::Vector3f result_color = {0, 0, 0};
//对于每一束光,需要计算phong模型下的光照结果
for (auto& light : lights)
{
// 光的方向
Eigen::Vector3f light_dir = light.position - point;
// 视线方向
Eigen::Vector3f view_dir = eye_pos - point;
// 衰减因子
float r = light_dir.dot(light_dir);
// ambient
Eigen::Vector3f La = ka.cwiseProduct(amb_light_intensity);
// diffuse
Eigen::Vector3f Ld = kd.cwiseProduct(light.intensity / r);
Ld *= std::max(0.0f, normal.normalized().dot(light_dir.normalized()));
// specular
Eigen::Vector3f h = (light_dir.normalized() + view_dir.normalized()).normalized();
Eigen::Vector3f Ls = ks.cwiseProduct(light.intensity / r);
Ls *= std::pow(std::max(0.0f, normal.normalized().dot(h)), p);
result_color += (La + Ld + Ls);
}
return result_color * 255.f;
} phong模型需要计算出每个点的漫反射、高光、环境光,如果对于公式有不理解的可以看[9]中的公式,这里不再介绍了。提示几点:
①光照方向和人眼方向向量都是从物体出发的,故都是-point
②半程向量h,是归一化后的light_dir和view_dir相加之后得到的方向,之后需再进行一次归一化,若前者没有归一化,得到的结果如下所示,这里参考了[10]。
③高光不忘记pow来控制高光范围,不然就会像下面一样太白啦
④注意vector3f或者vector4f以及max的等函数需要传入float类型的数据,请记得随手加上小数点哦
最终结果如下:
2.3 texture模型
// 纹理shader
Eigen::Vector3f texture_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f return_color = { 0, 0, 0 };
if (payload.texture)
{
// 获取纹理坐标的颜色
return_color = payload.texture->getColor(payload.tex_coords.x(), payload.tex_coords.y());
}
Eigen::Vector3f texture_color;
texture_color << return_color.x(), return_color.y(), return_color.z();
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = texture_color / 255.f; // 颜色归一化
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{ {20, 20, 20}, {500, 500, 500} };
auto l2 = light{ {-20, 20, 0}, {500, 500, 500} };
std::vector lights = { l1, l2 };
Eigen::Vector3f amb_light_intensity{ 10, 10, 10 };
Eigen::Vector3f eye_pos{ 0, 0, 10 };
float p = 150;
Eigen::Vector3f color = texture_color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = { 0, 0, 0 };
Eigen::Vector3f ambient = ka * amb_light_intensity[0];
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
Eigen::Vector3f light_dir = light.position - point;
Eigen::Vector3f view_dir = eye_pos - point;
float r = light_dir.dot(light_dir);
// ambient
Eigen::Vector3f La = ka.cwiseProduct(amb_light_intensity);
// diffuse
Eigen::Vector3f Ld = kd.cwiseProduct(light.intensity / r);
Ld *= std::max(0.0f, normal.normalized().dot(light_dir.normalized()));
// specular
Eigen::Vector3f h = (light_dir.normalized() + view_dir.normalized()).normalized();
Eigen::Vector3f Ls = ks.cwiseProduct(light.intensity / r);
Ls *= std::pow(std::max(0.0f, normal.normalized().dot(h)), p);
result_color += (La + Ld + Ls);
}
return result_color * 255.f;
}
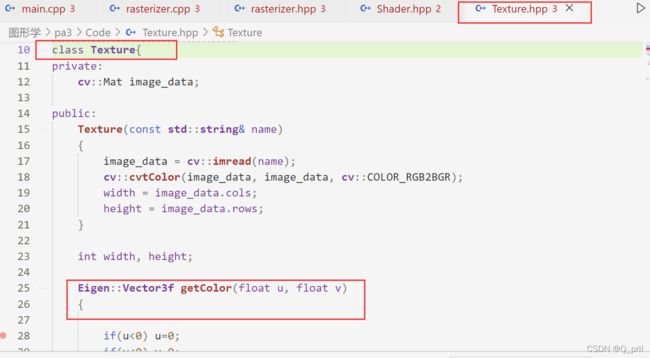
这个模型的特点是着色需要考虑纹理,那么纹理影响哪一步呢?没错就是颜色!而颜色用于漫反射,厘清这个关系就够了,这个模型比起phong模型只需把颜色改为当前像素对应的纹理即可。而纹理如何得到?payload模型中记录了纹理的坐标tex_coords和纹理Texture类,若想获取纹理值,只需把纹理坐标传到获取纹理的函数即可,这里注意厘清关系。
2.3.1 Segmentation fault
这里记录两个我遇到的问题,第一个是关于U、V坐标范围的,模型计算的UV会出现小于0或者大于1的情况,如下图所示,会导致Segmentation fault,在[11]中也有人说到这个问题,解决方式就是限制到0,1即可。
Eigen::Vector3f getColor(float u, float v)
{
if(u<0) u=0;
if(v<0) v=0;
if(u>1) u=1;
if(v>1) v=1;
auto u_img = u * width;
auto v_img = (1 - v) * height;
auto color = image_data.at(v_img, u_img);
return Eigen::Vector3f(color[0], color[1], color[2]);
} 2.3.2 libpng warning:iCCP:known incorrect sRGB profile
 第二个问题是在运行时出现的,简单来说,问题在于——Libpng-1.6在检查ICC配置文件方面比以前的版本更严格,可以忽略此警告、不影响程序的结果,如果想要解决,需要从PNG图像中删除ICCP块,参考:
第二个问题是在运行时出现的,简单来说,问题在于——Libpng-1.6在检查ICC配置文件方面比以前的版本更严格,可以忽略此警告、不影响程序的结果,如果想要解决,需要从PNG图像中删除ICCP块,参考:
c++ - libpng warning: iCCP: known incorrect sRGB profile - Stack Overflow
2.4 bump和displacement模型
这一部分其实在代码方面有一些超纲,所以也可以看到注释方面写的已经相当详尽了,根据论坛来看后续课程会再次详细解释原理,这里先不多赘述,展示代码如下:
Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement bump mapping here
// Let n = normal = (x, y, z)
// Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
// Vector b = n cross product t
// Matrix TBN = [t b n]
float x = normal.x();
float y = normal.y();
float z = normal.z();
Eigen::Vector3f t{ x * y / std::sqrt(x * x + z * z), std::sqrt(x * x + z * z), z*y / std::sqrt(x * x + z * z) };
Eigen::Vector3f b = normal.cross(t);
Eigen::Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
// dU = kh * kn * (h(u+1/w,v)-h(u,v))
// dV = kh * kn * (h(u,v+1/h)-h(u,v))
// Vector ln = (-dU, -dV, 1)
// Normal n = normalize(TBN * ln)
float u = payload.tex_coords.x();
float v = payload.tex_coords.y();
float w = payload.texture->width;
float h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColor(u + 1.0f / w , v).norm() - payload.texture->getColor(u, v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1.0f / h).norm() - payload.texture->getColor(u, v).norm());
Eigen::Vector3f ln{ -dU,-dV,1.0f };
normal = TBN * ln;
// 归一化
Eigen::Vector3f result_color = normal.normalized();
return result_color * 255.f;
}
Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement displacement mapping here
// Let n = normal = (x, y, z)
// Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
// Vector b = n cross product t
// Matrix TBN = [t b n]
float x = normal.x();
float y = normal.y();
float z = normal.z();
Eigen::Vector3f t{ x*y / std::sqrt(x*x + z * z), std::sqrt(x*x + z * z), z*y / std::sqrt(x*x + z * z) };
Eigen::Vector3f b = normal.cross(t);
Eigen::Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
// dU = kh * kn * (h(u+1/w,v)-h(u,v))
// dV = kh * kn * (h(u,v+1/h)-h(u,v))
// Vector ln = (-dU, -dV, 1)
// Position p = p + kn * n * h(u,v)
// Normal n = normalize(TBN * ln)
float u = payload.tex_coords.x();
float v = payload.tex_coords.y();
float w = payload.texture->width;
float h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColor(u + 1.0f / w, v).norm() - payload.texture->getColor(u , v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1.0f / h).norm() - payload.texture->getColor(u , v).norm());
Eigen::Vector3f ln{ -dU,-dV,1.0f };
point += (kn * normal * payload.texture->getColor(u , v).norm());
normal = TBN * ln;
normal = normal.normalized();
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
Eigen::Vector3f light_dir = light.position - point;
Eigen::Vector3f view_dir = eye_pos - point;
float r = light_dir.dot(light_dir);
// ambient
Eigen::Vector3f La = ka.cwiseProduct(amb_light_intensity);
// diffuse
Eigen::Vector3f Ld = kd.cwiseProduct(light.intensity / r);
Ld *= std::max(0.0f, normal.dot(light_dir.normalized()));
// specular
Eigen::Vector3f h = (light_dir.normalized() + view_dir.normalized()).normalized();
Eigen::Vector3f Ls = ks.cwiseProduct(light.intensity / r);
Ls *= std::pow(std::max(0.0f, normal.dot(h)), p);
result_color += (La + Ld + Ls);
}
return result_color * 255.f;
} 补充两点,首先bump是只改变了法向向量以此营造出凹凸贴图的感觉,而displacement是改变了点的位置进而也改变了法线。其次,注意注释中有的是向量,有的是矩阵,二者在赋值、初始化时方式有些许不同。另外在这方面有疑问或想现在就搞明白的可以参考[12]、[13]。
3.0 提高部分:双线性插值:
当纹理过小时,会导致很多像素都选取了同一个纹理,进而出现锯齿等情况,如下图所示为我打印出的各个像素的颜色,可以看到存在较多像素颜色相同的情况。
通过双线性插值即可得到模糊、平滑后的结果,如下图所示,最右边为1024x1024的纹理图得到的效果,相对光滑;最左边为512x512纹理图的结果,中间为512x512纹理图下双线性插值的结果,相对最左边的要平滑一些,更接近最右边的结果。
代码如下,原理不再解释,使用的时候记得修改main.cpp中的texture函数哦:
Eigen::Vector3f getColorBilinear(float u, float v)
{
if(u<0) u=0;
if(v<0) v=0;
if(u>1) u=1;
if(v>1) v=1;
auto u_img = u * (width);
auto v_img = (1 - v) * (height);
float u0 = std::max(1.0,floor(u_img-0.5)), u1 = floor(u_img+0.5);
float v0 = std::max(1.0,floor(v_img-0.5)), v1 = floor(v_img+0.5);
float s = (u_img-u0)/(u1-u0);
float t = (v_img-v0)/(v1-v0);
auto color00 = image_data.at(v0, u0);
auto color01 = image_data.at(v0, u1);
auto color10 = image_data.at(v1, u0);
auto color11 = image_data.at(v1, u1);
auto color0 = color00 + s*(color01-color00);
auto color1 = color10 + s*(color11-color10);
auto color = color0 + t*(color1-color0);
return Eigen::Vector3f(color[0], color[1], color[2]);
} 4.0 结语
这真的是我做过最认真的普通作业了,虽然在这个过程中查阅了很多资料,但其实还是有一些小问题,比如我的牛在嘴左侧有一颗黑点...比如bump和displacement模型并没有搞得很清楚...博客里也有不少东西是我自行理解的,如果有问题或者如果还有更好的效果、写法,可以告诉我~
下方的链接是论坛中关于作业三的所有帖子,希望可以帮助大家,也免去一页一页翻帖子了哈哈~
计算机图形学与混合现实研讨会
参考链接
[1]GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibili
[2]GAMES101现代计算机图形学入门 渲染管线(Graphics Pipeline) - 知乎
[3]作业3 interpolated_shadingcoords – 计算机图形学与混合现实研讨会
[4]【图形学】GAMES101 Assignment3 作业框架分析_Mine268的博客-CSDN博客
[5]图形学基础知识:重心坐标(Barycentric Coordinates)_王王王渣渣的博客-CSDN博客_重心坐标
[6]关于作业2和作业3中Z-Buffer的问题 – 计算机图形学与混合现实研讨会
[7]作业3 关于深度值问题自己踩的坑和一些想法 – 计算机图形学与混合现实研讨会
[8]GAMES101-现代计算机图形学学习笔记(作业03)_CCCCCCros____的博客-CSDN博客_games101作业3[9]GAMES101 闫令琪图形学 作业3_再学一个我就睡的博客-CSDN博客_games101 作业3[9]作业3phong模型的高亮位置不对 – 计算机图形学与混合现实研讨会
[11]作业3:UV坐标取值范围 – 计算机图形学与混合现实研讨会
[12]计算机图形学八:纹理映射的应用(法线贴图,凹凸贴图与阴影贴图等相关应用的原理详解) - 知乎关于作业三的dispalcement map – 计算机图形学与混合现实研讨会
[14]作业3双线性插值后效果更差了 – 计算机图形学与混合现实研讨会
[15]作业3踩坑分享 – 计算机图形学与混合现实研讨会