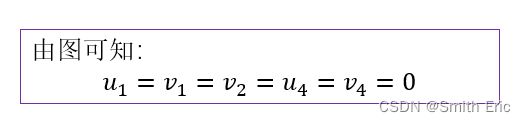Matlab-四杆桁架结构的有限元分析(有限元分析基础-曾攀)

 

求解步骤如下:

程序见最后

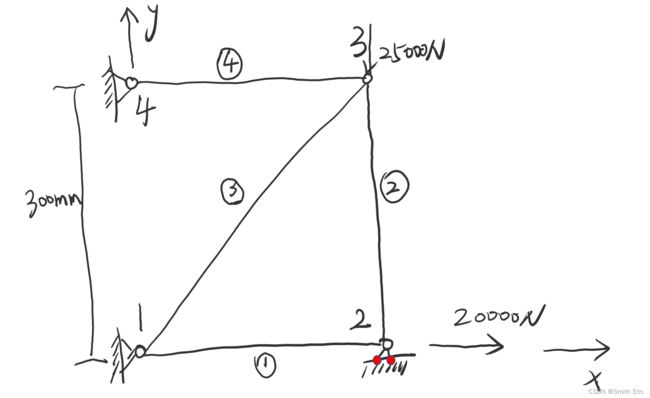
Step1:结构离散和编号

Step2:计算各单元的刚度矩阵

        输入弹性模量、横截面积、坐标位置、夹角等参数

        代入程序分别求得四个单元刚度矩阵（k1.k2,k3,k4）

Step3:建立整体刚度方程

%四个节点，共8个自由度
>>KK=zeros(8,8);
%分别对号入座，代入总刚矩阵
>>KK=Bar2D2Node_Assembly(KK,k1,1,2);
>>KK=Bar2D2Node_Assembly(KK,k2,2,3);
>>KK=Bar2D2Node_Assembly(KK,k3,1,3);
>>KK=Bar2D2Node_Assembly(KK,k4,3,4);

Step4:施加边界条件以及刚度方程求解

>>k=KK([3,5,6],[3,5,6]);
>>p=[20000;0;-25000];
>>u=k\p;

 将u和和上图组合得到所有节点位移q

Step5:支反力的计算

%支反力为
P=KK*q

Step6:各个单元的应力计算

先从整体位移列阵q中提取单元的位移列阵

调用计算单元应力的函数Bar2DNode_Stress得到各个单元的应力分量

>>u1=[q(1);q(2);q(3);q(4)]
>>stress1=Bar2DNode_Stress(E,A,x1,y1,x2,y2,alpha1,u1)

>>u2=[q(3);q(4);q(5);q(6)]
>>stress2=Bar2DNode_Stress(E,A,x2,y2,x3,y3,alpha2,u2)

>>u3=[q(1);q(2);q(5);q(6)]
>>stress3=Bar2DNode_Stress(E,A,x,y1,x3,y3,alpha3,u3)

>>u4=[q(7);q(8);q(5);q(6)]
>>stress4=Bar2DNode_Stress(E,A,x4,y4,x3,y3,alpha4,u1)

%计算全局刚度矩阵
function k=Bar2D2Node_Stiffness(E,A,x1,y1,x2,y2,alpha)
%该函数计算单元的刚度矩阵
%input:弹性模量W、横截面积A
%input：第一个节点坐标(x1,y1)、第二个节点坐标（x2,y2）和角度alpha
%output:输出单元刚度矩阵k(4x4)
%----------------------------------------------------
L=sqrt((x2-x1)^2+(y2-y1)^2);
x=alpha*pi/180;
C=cos(x); S=sin(x);
k=E*A/L*[C*C C*S -C*C -C*S;
         C*S S*S -C*S -S*S;
        -C*C -C*S C*C  C*S;
        -C*S -S*S C*S  S*S];

%该函数计算单元的应力
function stress=Bar2D2Node_Stress(E,x1,y1,x2,y2,alpha,u)
%input:E;第一个节点坐标;第二个节点坐标
%input:夹角alpha，节点位移向量u
%返回单元应力值stress
%----------------------
L=sqrt((x2-x1)^2+(y2-y1)^2);
x=alpha*pi/180;
C=cos(x); S=sin(x);
Stress=E/L*[-C -S C S]*u;

组装总刚度矩阵见

Matlab-杆单元整体刚度矩阵组装（有限元基础-曾攀）_Smith Eric的博客-CSDN博客https://blog.csdn.net/qq_39642029/article/details/124491784?spm=1001.2014.3001.5502