第二章 多变量线性回归

1.多维特征

多维特征是指数据集中包含多个特征或变量的数据，每个特征都可以描述数据对象的某一方面。在机器学习中，多维特征通常用于训练模型进行分类、回归或聚类等任务。

在处理多维特征时，需要注意一些问题。首先，有些特征之间可能存在相关性，这会导致模型过拟合。因此，需要进行特征选择或降维处理，以去除冗余特征或减少特征间的相关性。其次，不同特征的尺度或量纲可能不同，需要进行归一化或标准化处理，以使所有特征都在同一量纲上。此外，对于缺失值或异常值需要进行处理，以避免对模型训练造成影响。

在多维特征的应用中，可以考虑使用一些高级技术来处理高维数据。例如，基于核的方法可以将高维数据映射到低维空间，同时保持数据的结构；随机森林或梯度提升机等集成方法也可以用于处理多维特征；基于矩阵分解的方法可以将高维特征矩阵分解为多个低维矩阵的乘积，从而实现降维；另外，还有基于距离度量或相似度度量的方法，如主成分分析（PCA）等。

总之，多维特征是机器学习中常见的数据形式，需要采取适当的方法进行处理和利用，以提高模型的性能和泛化能力。

2.多变量梯度下降

与单变量线性回归类似，在多变量线性回归中，我们也构建一个代价函数，则这个代价
函数是所有建模误差的平方和，即


我们开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

多变量梯度下降（Gradient Descent for Multiple Variables）是梯度下降算法在多变量问题上的应用。在多变量梯度下降中，我们需要同时优化多个参数，以最小化目标函数（通常是代价函数）。

与单变量梯度下降相比，多变量梯度下降需要考虑多个参数的变化方向和步长。在每次迭代中，我们需要计算目标函数对每个参数的偏导数（梯度），然后根据所有参数的梯度来更新参数。
具体来说，多变量梯度下降的步骤如下：
1.初始化参数向量θ为一个随机值或者全零向量。
2.计算目标函数对于参数向量的梯度。
3.根据梯度方向和步长更新参数向量θ。
4.重复步骤2和3，直到达到预设的停止条件（如梯度小于某个阈值，或者达到预设的最大迭代次数）。
在多变量梯度下降中，步长的选择也是一个关键因素。常见的步长选择方法包括固定步长、学习率衰减等。选择合适的步长可以影响算法的收敛速度和最终的结果。

此外，为了避免算法陷入局部最小值，可以采用一些策略，如使用不同的初始参数值、随机初始化参数向量、多次运行算法并选择最优结果等。

总之，多变量梯度下降是一种常用的优化算法，适用于多变量问题。通过迭代更新参数向量，它可以找到目标函数的局部最小值，并用于机器学习和深度学习等领域中的模型训练和参数优化。

3.梯度下降法实践 1-特征缩放

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯
度下降算法更快地收敛。
以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-
2000 平方英尺，而房间数量的值则是 0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

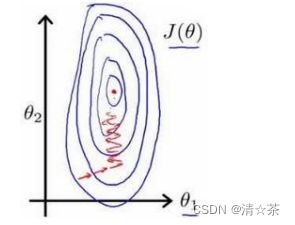
解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。如图：


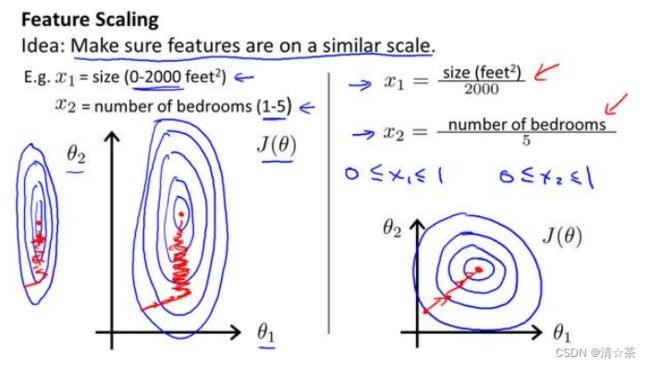
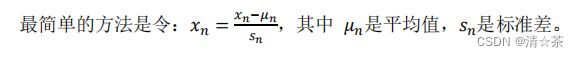
保证值在-1到1之间。
在实践中，梯度下降法常常需要配合特征缩放来进行。特征缩放的主要目的是将不同尺度的特征值缩放到同一尺度上，从而保证梯度下降法能够更有效地收敛。

具体来说，如果特征值的取值范围差异很大，梯度下降算法在迭代过程中可能会在取值范围较小的特征上快速收敛，而忽略取值范围较大的特征。为了避免这种情况，我们需要将所有特征的尺度进行统一。

特征缩放的方法有很多种，常见的一种是归一化，即将特征值减去均值然后除以取值范围，得到标准化的特征值。这种方法的优点是可以将所有特征的取值范围控制在-1到1之间，方便计算和比较。

另一种常用的特征缩放方法是使用对数变换或者多项式变换等非线性变换方法，将特征值映射到指定的范围内。这些方法适用于特征值的分布不符合正态分布的情况。

在实践中，选择哪种特征缩放方法需要具体问题具体分析。一般来说，如果特征值的分布比较均匀且符合正态分布，可以选择归一化方法；如果特征值的分布不均匀或者不符合正态分布，可以选择非线性变换方法。

需要注意的是，在进行特征缩放时需要保持原始数据的分布特性，不能因为缩放导致数据的分布发生改变，从而影响模型的性能和结果的可靠性。

4. 梯度下降法实践 2-学习率

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们
可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

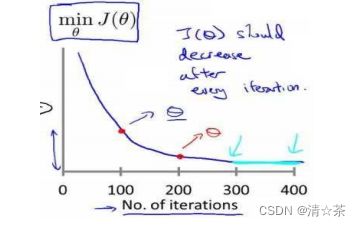
梯度下降算法的每次迭代受到学习率的影响，如果学习率过小，则达到收敛所需的迭
代次数会非常高；如果学习率过大，每次迭代可能不会减小代价函数，可能会越过局部最
小值导致无法收敛。

学习率在梯度下降法中是一个关键参数，它决定了每次迭代时参数更新的步长。学习率的选择对梯度下降法的性能和收敛速度有着重要影响。

在实践中，选择合适的学习率是非常重要的。如果学习率过大，可能会导致梯度下降算法无法收敛，甚至越过局部最小值；如果学习率过小，则可能导致算法收敛速度过慢，需要更多的迭代次数。

一种常见的学习率选择方法是尝试不同的学习率值，然后观察算法的收敛情况。通常可以尝试一些固定的学习率值，例如0.01、0.03、0.1、0.3、1等，然后绘制代价函数随迭代步数的变化曲线。如果发现学习率过大或过小，可以相应地调整学习率值，直到找到一个合适的学习率。

另外，也可以使用动态调整学习率的方法，例如自适应学习率算法。这种算法会根据梯度下降算法的收敛情况自动调整学习率，从而更好地控制参数更新的步长。

总之，选择合适的学习率是梯度下降法实践中的关键步骤之一。需要仔细选择和调整学习率，以确保梯度下降算法能够快速、有效地收敛，并得到最优的参数解。

5.特征和多项式回归

特征缩放是实际应用线性回归模型时的一个重要步骤。当我们在处理具有多个特征的数据时，可能会发现不同特征的取值范围差异很大。这就可能导致梯度下降算法在迭代过程中，由于维度之间的差异使得Jθ的值收敛得很慢，甚至无法收敛。

为了解决这个问题，我们通常采用特征缩放，也就是将所有的特征都缩放到一个相近的取值范围内。例如，我们可以将特征值减去其均值，然后除以取值范围，进行标准化处理。这样，所有的特征都在-1到1的范围内，梯度下降法就能更快地收敛。

以一个具体的例子来说明，假设我们有两个特征x1和x2，其中x1的取值范围在0-2000之间，而x2的取值范围在1-5之间。如果我们直接使用这两个特征进行线性回归，梯度下降法可能会非常慢。但是，如果我们把这两个特征都缩放到0-1之间，那么梯度下降法就会更快地收敛。

6.正规方程

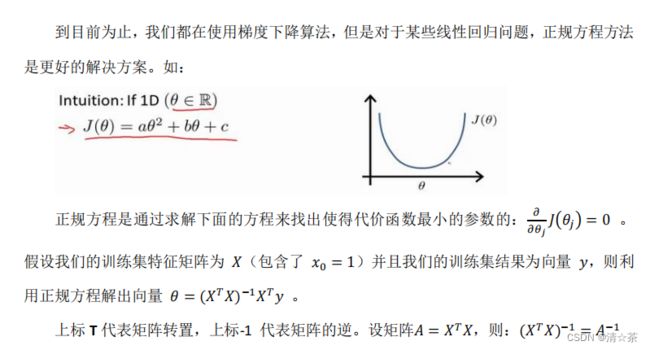
注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺
寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是
不能用的。

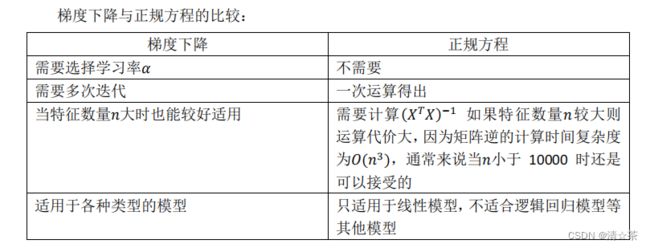
对于那些更复杂的学习算法，
我们将不得不仍然使用梯度下降法。因此，梯度下降法是一个非常有用的算法，可以用在有
大量特征变量的线性回归问题。或者我们以后在课程中，会讲到的一些其他的算法，因为标
准方程法不适合或者不能用在它们上。但对于这个特定的线性回归模型，标准方程法是一个
比梯度下降法更快的替代算法。所以，根据具体的问题，以及你的特征变量的数量，这两种
算法都是值得学习的。

正规方程是一种求解线性回归参数的方法，它通过求解一个线性方程组来找到最优的参数。正规方程的优点在于它可以避免梯度下降等优化算法中的迭代过程，从而更快地得到参数解。

在正规方程中，我们首先将训练数据和结果进行矩阵表示。假设训练数据有m个样本，每个样本有n个特征，则可以将其表示为m×n的矩阵X，结果可以表示为m×1的向量y。然后，我们通过求解正规方程组来找到最优的参数向量θ。正规方程组可以表示为：

X^T * X * θ = X^T * y

其中，X^T表示矩阵X的转置，θ表示参数向量，y表示结果向量。

通过求解正规方程组，我们可以得到最优的参数向量θ。这种方法在理论上比梯度下降等优化算法更快，因为它只需要求解一个线性方程组，而不是通过迭代逐步逼近最优解。

然而，在实际应用中，正规方程可能会受到一些限制。例如，当特征之间存在多重共线性时，即多个特征之间存在高度的线性相关性，正规方程可能会变得不稳定，因为它会试图同时拟合这些高度相关的特征。此时，使用梯度下降等优化算法可能会更加稳定和可靠。

综上所述，正规方程是一种求解线性回归参数的方法，通过求解一个线性方程组来找到最优的参数。它具有理论上的优势，但在实际应用中可能会受到限制。选择使用哪种方法需要根据具体情况而定。

7.Octave 教程(Octave Tutorial)

最多的用于机器学习的原始语言是 Octave、MATLAB、Python、NumPy和 R。
加减乘除：±*/
或与非：or、&&、||
打印输出用disp(a),a为参数。
创建向量：
V=1：0.1：2
这个该如何理解呢：这个集合是一组值，从数值 1 开始，增量或说是步长为 0.1，直到
增加到 2，按照这样的方法对向量操作，可以得到一个行向量，这是一个 1 行 11 列的矩
阵，其矩阵的元素是 1 1.1 1.2 1.3，依此类推，直到数值 2。
可以建立一个集合并用命令“1:6”进行赋值，这样就被赋值了1 至6 的六个整数。

这里还有一些其他的方法来生成矩阵
例如“ones(2, 3)”，也可以用来生成矩阵：

元素都为 2，两行三列的矩阵，就可以使用这个命令：

为一个一行三列的零矩阵，一行三列的矩阵里的元素全部是零：

如果我对进行赋值，用 Rand 命令建立一个一行三列的矩阵，因为使用了 Rand 命令，
则其一行三列的元素均为随机值，如“rand(3,3)”命令，这就生成了一个 3×3 的矩阵，并且其所有元素均为随机。

数值介于 0 和 1 之间，所以，正是因为这一点，我们可以得到数值均匀介于 0 和 1 之间
的元素。如果，你知道什么是高斯随机变量，或者，你知道什么是正态分布的随机变量，你可以设置集合，使其等于一个一行三列的
分布，方差或者等于矩阵，并且，来自三个值，一个平均值为 0 的高斯分布，方差或者等于1的标准偏差。

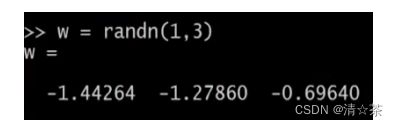
并用 hist 命令绘制直方图。

绘制单位矩阵：

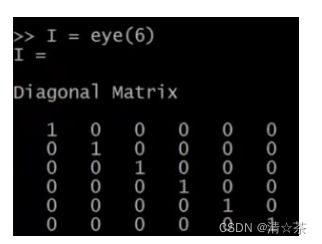
如果对命令不清楚，建议用 help 命令：

size() 命令返回矩阵的尺寸。

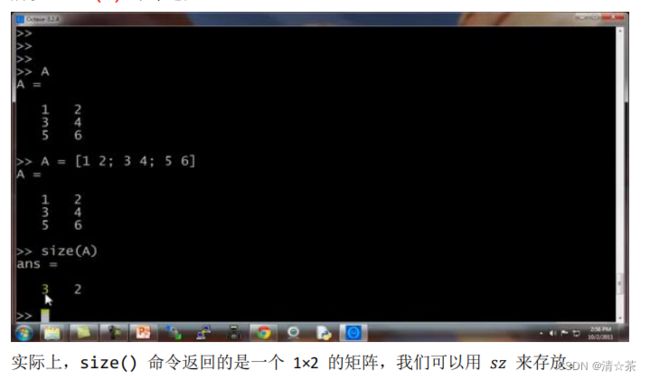
如果你有一个向量 ，假如 v = [1 2 3 4]，然后键入 length(v)，这个命令将返回最大维度的大小，返回 4。
pwd 命令可以显示出 Octave 当前所处路径。
cd 命令，意思是改变路径，我可以把路径改为 C:\Users\ang\Desktop，
ls列出当前文件夹中的所有文件。
who 函数能让你看到当前工作空间中的所有变量，同样还有另一个 whos 命令，能更
详细地进行查看。
把它存入硬盘，那么用 save hello.mat v 命令，这个命令会将变量存
成一个叫 hello.mat 的文件，让我们回车，现在我的桌面上就出现了一个新文件，名为
hello.mat。

A([1 3]，这个命令意思是取 矩阵第一个索引值为 1 或 3 的元素，也就是说我取的是 A 矩阵的第一行和第三行的每一列，冒号表示的是取这两行的每一列元素。

A = [A, [100; 101;102]]，这样做的结果是在
原矩阵的右边附加了一个新的列矩阵，就是把 矩阵设置为原来的 矩阵再在右边附上一
个新添加的列矩阵。

如果你就输入 A(，这是一个很特别的语法结构，意思是把中的所有元素放入一个单独的列向量。

C = [A B]，这个意思就是把这两个矩阵直接连在一起，矩阵 在左边，矩阵 在右边，这样组成了 矩阵，就是直接把和 合起来。

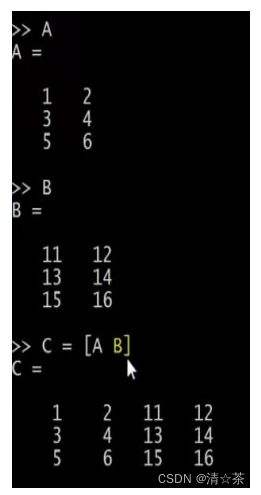
C = [A; B]，这里的分号表示把分号后面的东西放到下面。所以，[A;B]的作用依然还是把两个矩阵放在一起，只不过现在是上下排列，所以现在 在上面，在下面， 就是一个 6×2 矩阵。

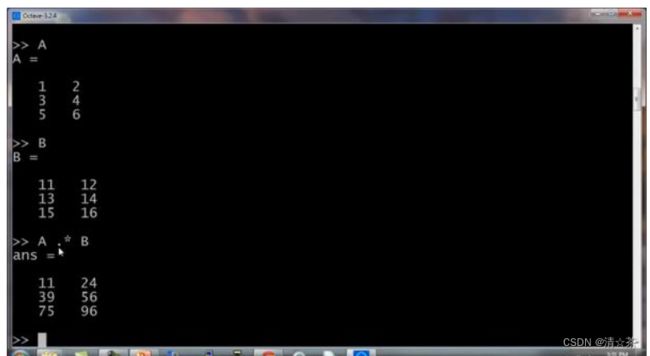
可以对每一个元素，做运算 方法是做点乘运算 A.*B，这么做 Octave 将矩阵 中的每一个元素与矩阵 中的对应元素相乘:A.*B
这里第一个元素 1 乘以 11 得到 11，第二个元素 2 乘以 12 得到 24，这就是两个矩阵的
元素位运算。通常来说，在 Octave 中点号一般用来表示元素位运算。

我输入 A.^2，这将对矩阵中每一个元素平方。

我们设为 [1; 2; 3] 是列向量，你也可以输入 1./V，得到每一个元素的倒数，所以这
样一来，就会分别算出 1/1 1/2 1/3。
矩阵也可以这样操作，1./A 得到中每一个元素的倒数。

abs求绝对值，-v是直接求负数。
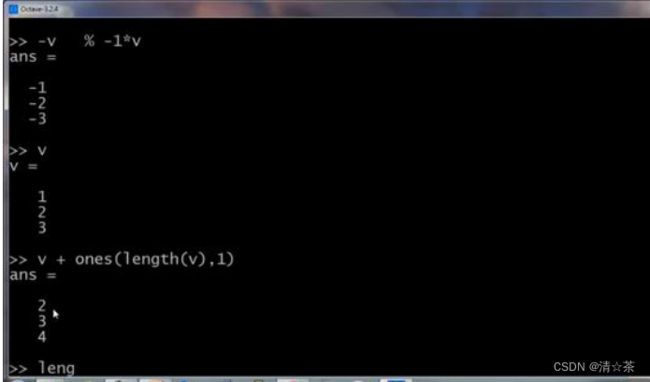
还有一个技巧，比如说我们想对中的每个元素都加 1，那么我们可以这么做，首先构
造一个 3 行 1 列的 1 向量，然后把这个 1 向量跟原来的向量相加，因此向量从[1 2 3] 增至[2 3 4]。我用了一个，length(v)命令，因此这样一来，ones(length(v) ,1) 就相当于
ones(3,1)，然后我做的是 v +ones(3,1)，也就是将 的各元素都加上这些 1，这样就
将 的每个元素增加了 1。

max是求当前矩阵的最大值。
v+1是矩阵中的每个元素都加1.
如果我写 find(a<3)，这将告诉我 中的哪些元素是小于 3 的。

设 A = magic(3)，magic 函数将返回一个矩阵，称为魔方阵或幻方 (magic squares)，它们具有以下这样的数学性质：它们所有的行和列和对角线加起来都等于相同的值。

sum(a)求和。
prod(a)矩阵中所有元素的乘积。
floor(a) 是向下四舍五入，因此对于 中的元素 0.5 将被下舍入变成 0。
ceil(a)，表示向上四舍五入，所以 0.5 将上舍入变为最接近的整数，也就是 1。
type(3)，这通常得到一个 3×3 的矩阵，如果键入 max(rand(3),rand(3))，这样做的结果是返回两个 3×3 的随机矩阵，并且逐元素比较取最大值。
flipup/flipud 表示向上/向下翻转。
算的对角线元素的和。我们现在构造一个 9×9 的单位矩阵，键入 eye(9)，然后我们要用 逐点乘以这个单位矩阵，除了对角线元素外，其他元素都会得到 0。键入 sum(sum(A.*eye(9))。
绘图数据：

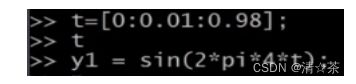
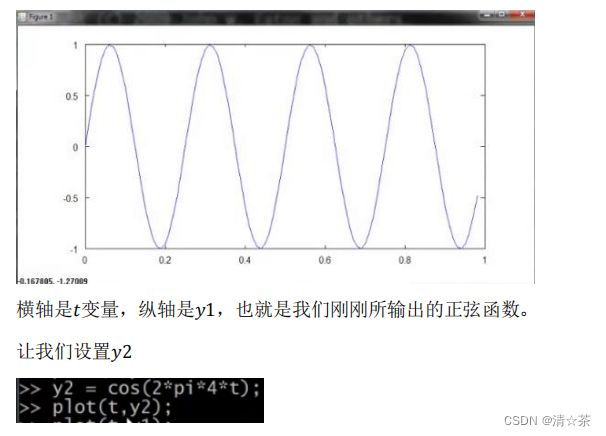
如果我想绘制正弦函数，这是很容易的，我只需要输入 plot(t,y1)，并回车，就出现
了这个图：



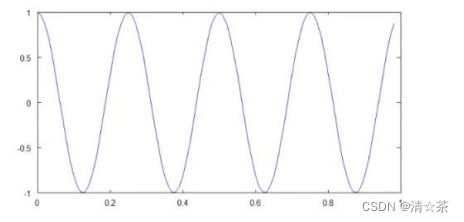
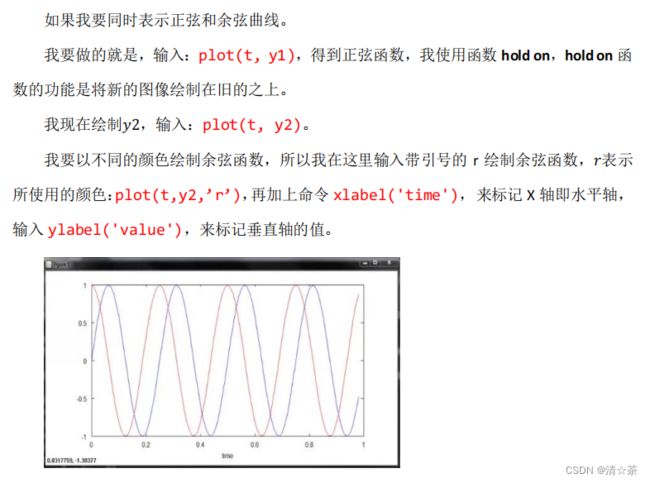
同时我也可以来标记我的两条函数曲线，用这个命令 legend(‘sin’,‘cos’)将这个图例放在右上方，表示这两条曲线表示的内容。最后输入 title(‘myplot’)，在图像的顶部显示这幅图的标题。
你键入 figure(1); plot(t, y1);将显示第一张图，绘制了变量 1。
键入 figure(2); plot(t, y2); 将显示第一张图，绘制了变量 2。
subplot 命令，我们要使用 subplot(1,2,1)，它将图像分为一个 1*2 的格子，也就是前两个参数，然后它使用第一个格子，也就是最后一个参数 1 的意思。

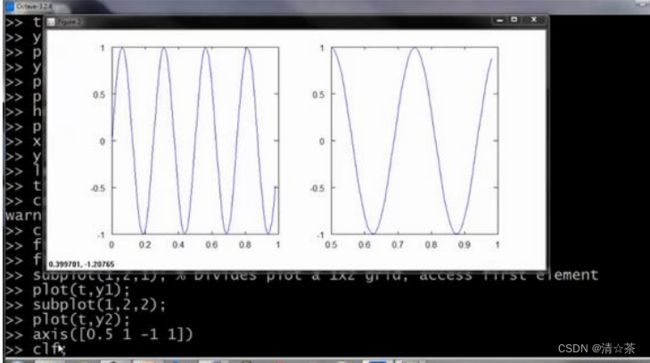
最后一个命令，你可以改变轴的刻度，比如改成[0.5 1 -1 1]，输入命令：axis([0.5 1 -1 1])也就是设置了右边图的轴和轴的范围。具而言，它将右图中的横轴的范围调整至 0.5 到 1，竖轴的范围为-1 到 1。
Clf（清除一幅图像）。
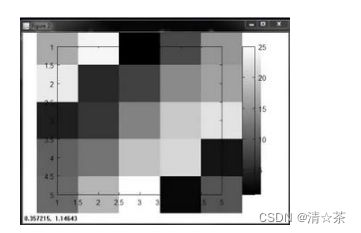
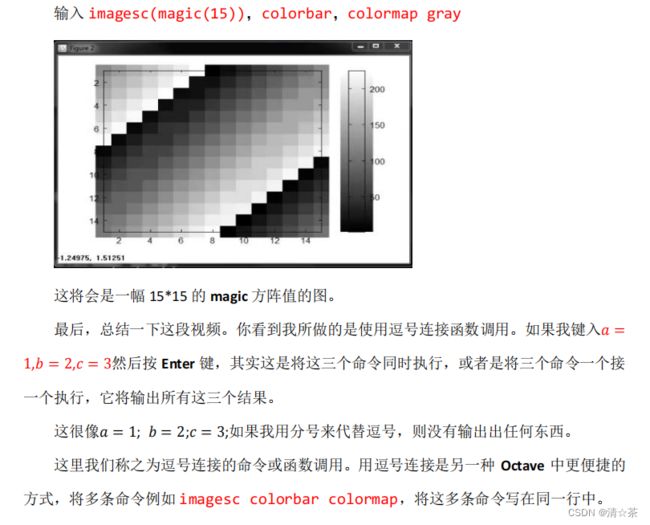
使用函数 colorbar，让我用一个更复杂的命令 imagesc(A)，colorbar，colormap gray。这实际上是在同一时间运行三个命令：运行 imagesc，然后运行，colorbar，然后运行 colormap gray。它生成了一个颜色图像，一个灰度分布图，并在右边也加入一个颜色条。所以这个颜色条显示不同深浅的颜色所对应的值。


控制语句：for,while,if语句
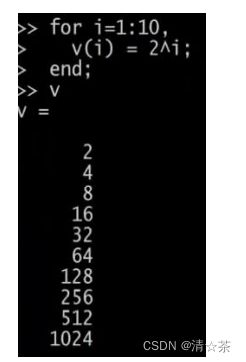
向量 的值就是这样一个集合 2 的一次方、2 的二次方，依此类推。这就是我的 等于 1 到 10 的语句结构，让 遍历 1 到 10 的值。





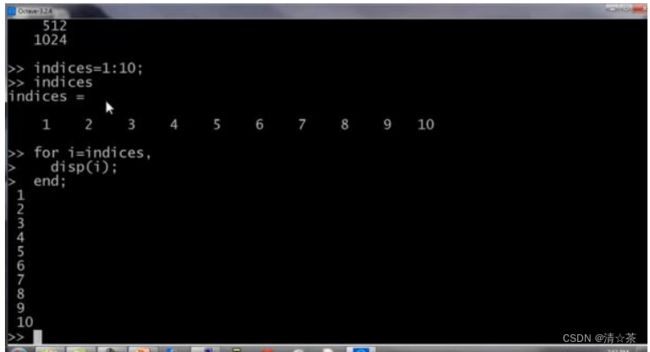
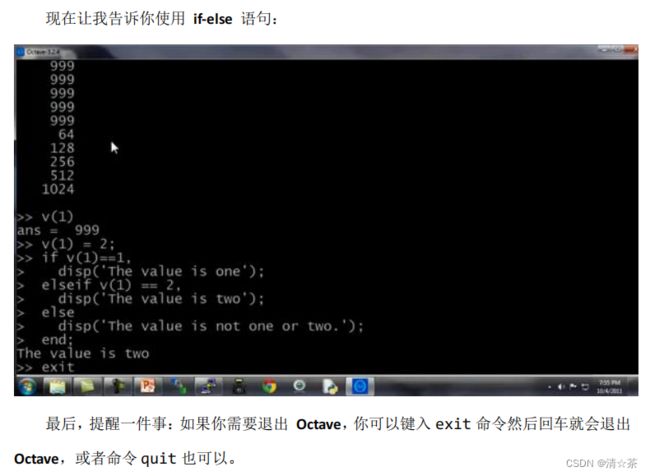
“SquareAndCubeThisNumber(x)” (的平方以及的立方)
这说的就是函数返回值是两个： 1 和 2，接下来就是1是被平方后的结果，2是被立方后的结果，这就是说，函数会真的返回 2 个值。
如果我键入 [a,b] = SquareAndCubeThisNumber(5)，然后，就等于 25， 就等于 5 的立方 125。

8.向量化

向量化就是编程简化，算法优化。
向量化是一种编程技巧，尤其在深度学习领域中，它被广泛应用。向量化是通过使用数学表达式来描述计算过程，从而避免使用显式的循环结构，以提高代码运行效率。

在深度学习中，尤其是在处理大数据集时，代码的运行速度至关重要。如果使用传统的循环结构来进行计算，可能会非常耗时。而向量化通过将计算过程表示为数学表达式，可以利用高级数学库（如NumPy）进行优化，从而显著提高代码运行速度。

向量化在实践中有很多应用。例如，在机器学习中，可以使用向量化来快速计算损失函数和梯度。在深度学习中，全连接神经网络的权重更新也可以通过向量化来实现。

总的来说，向量化是一种编程技巧，通过使用数学表达式来描述计算过程，可以避免使用显式的循环结构，从而提高代码运行效率。在深度学习领域中，向量化是一个关键的技巧，它能够显著提高代码运行速度，使得大数据集的处理成为可能。