机器学习系统的设计(Machine Learning System Design)

1.首先要做的内容

本章以一个垃圾邮件分类器算法为例进行讨论。
为了解决这样一个问题，我们首先要做的决定是如何选择并表达特征向量。我们可以选择一个由 100 个最常出现在垃圾邮件中的词所构成的列表，根据这些词是否有在邮件中出现，来获得我们的特征向量（出现为 1，不出现为 0），尺寸为 100×1。
为了构建这个分类器算法，我们可以做很多事，例如：

1. 收集更多的数据，让我们有更多的垃圾邮件和非垃圾邮件的样本
2. 基于邮件的路由信息开发一系列复杂的特征
3. 基于邮件的正文信息开发一系列复杂的特征，包括考虑截词的处理
4. 为探测刻意的拼写错误（把 watch 写成 w4tch）开发复杂的算法。

在上面这些选项中，非常难决定应该在哪一项上花费时间和精力，作出明智的选择，比随着感觉走要更好。将在随后的课程中学习误差分析，将会了解到怎样用一个更加系统性的方法，从一堆不同的方法中，选取合适的那一个。

2.误差分析

构建一个学习算法的推荐方法为：

1. 从一个简单的能快速实现的算法开始，实现该算法并用交叉验证集数据测试这个算法。
2. 绘制学习曲线，决定是增加更多数据，或者添加更多特征，还是其他选择。
3. 进行误差分析：人工检查交叉验证集中我们算法中产生预测误差的实例，看看这些实例是否有某种系统化的趋势。
   以我们的垃圾邮件过滤器为例，误差分析要做的既是检验交叉验证集中我们的算法产生错误预测的所有邮件，看：是否能将这些邮件按照类分组。例如医药品垃圾邮件，仿冒品垃圾邮件或者密码窃取邮件等。然后看分类器对哪一组邮件的预测误差最大，并着手优化。
   思考怎样能改进分类器。例如，发现是否缺少某些特征，记下这些特征出现的次数。
   例如记录下错误拼写出现了多少次，异常的邮件路由情况出现了多少次等等，然后从出现次数最多的情况开始着手优化。
   吴恩达的机器学习误差分析方法可以总结如下：
   1.收集误差样本：从模型的预测结果中选择一组样本，这些样本可能被错误分类或者模型在这些样本上表现不佳。
   2.分析误差类型：针对每个误差样本，确定其错误类型，如假阳性、假阴性、误分类等。
   3.确定误差来源：通过仔细观察和分析误差样本，寻找造成误差的潜在原因。这可能涉及到数据集问题（如标签错误、噪声数据）、模型问题（如欠拟合、过拟合）以及特征工程等方面。
   4.制定改进策略：根据误差分析的结果，制定相应的改进策略。这包括调整模型超参数、增加更多训练数据、改进特征工程、使用更复杂的模型结构等。
   5.实施改进措施：根据制定的改进策略，对模型进行相应的修改和优化，并重新训练和评估模型的性能。
   6.迭代反复：误差分析是一个迭代的过程，需要不断进行反馈和改进。通过不断分析误差、改进模型，逐步提高模型的性能。

吴恩达强调误差分析的重要性，认为它是改进和优化模型的关键一步。通过仔细分析模型的错误，我们可以了解模型的弱点，并采取相应的措施来修复和提升模型的性能。误差分析需要结合领域知识和实践经验，需要在实践中不断进行反复和迭代。最终，通过不断的误差分析和改进，可以构建出更准确、鲁棒的机器学习模型。

3.类偏斜的误差度量

使用一个合适的误差度量值，这有时会对于你的学习算法造成非常微
妙的影响，这件重要的事情就是偏斜类（skewed classes）的问题。类偏斜情况表现为我们的训练集中有非常多的同一种类的实例，只有很少或没有其他类的实例。
例如我们希望用算法来预测癌症是否是恶性的，在我们的训练集中，只有 0.5%的实例是恶性肿瘤。假设我们编写一个非学习而来的算法，在所有情况下都预测肿瘤是良性的，那么误差只有 0.5%。然而我们通过训练而得到的神经网络算法却有 1%的误差。这时，误差的大小是不能视为评判算法效果的依据的。
查准率（Precision）和查全率（Recall） 我们将算法预测的结果分成四种情况：

1. 正确肯定（True Positive,TP）：预测为真，实际为真
2. 正确否定（True Negative,TN）：预测为假，实际为假
3. 错误肯定（False Positive,FP）：预测为真，实际为假
4. 错误否定（False Negative,FN）：预测为假，实际为真
   则：查准率=TP/(TP+FP)。例，在所有我们预测有恶性肿瘤的病人中，实际上有恶性肿瘤的病人的百分比，越高越好。
   查全率=TP/(TP+FN)。例，在所有实际上有恶性肿瘤的病人中，成功预测有恶性肿瘤的病人的百分比，越高越好。
   吴恩达在机器学习中提到了一种用于处理类偏斜（class imbalance）问题的误差度量方法，即使用精确度（precision）和召回率（recall）的组合来评估模型性能。

类偏斜问题是指在分类问题中，不同类别的样本数量差异很大，其中一个类别的样本数量远多于另一个类别。这样的情况下，简单地使用准确度作为评估指标可能会产生误导性的结果。

在类偏斜的情况下，吴恩达建议使用精确度和召回率来更全面地评估模型的性能。精确度是指被正确分类的正样本占所有被分类为正样本的样本的比例，而召回率是指正确分类的正样本占所有实际正样本的比例。

具体来说，对于类别为正例的样本，精确度衡量了模型在预测正例时的准确性，而召回率衡量了模型对于实际正例的覆盖程度。在类偏斜的情况下，我们更关注模型对于少数类别的预测性能，因此可以将召回率作为主要的评估指标。

此外，吴恩达还提到了F1分数（F1 score），它是精确度和召回率的加权调和平均值。F1分数综合考虑了模型的精确度和召回率，适用于在类别偏斜问题中对模型性能进行综合评估。

总结来说，吴恩达建议在类偏斜问题中使用精确度、召回率和F1分数来评估模型的性能，以获得更全面和准确的结果。这种方法能够更好地处理类别不平衡带来的挑战，并提供更具实际意义的模型评估。

4.查准率和查全率之间的权衡

希望能够保证查准率和召回率的相对平衡。
预测肿瘤性质的例子。假使，我们的算法输出的结果在 0-1 之间，我们使用阀值 0.5 来预测真和假。

查准率(Precision)=TP/(TP+FP) 例，在所有我们预测有恶性肿瘤的病人中，实际上有恶性肿瘤的病人的百分比，越高越好。
查全率(Recall)=TP/(TP+FN)例，在所有实际上有恶性肿瘤的病人中，成功预测有恶性肿瘤的病人的百分比，越高越好。
如果我们希望只在非常确信的情况下预测为真（肿瘤为恶性），即我们希望更高的查准率，我们可以使用比 0.5 更大的阀值，如 0.7，0.9。这样做我们会减少错误预测病人为恶性肿瘤的情况，同时却会增加未能成功预测肿瘤为恶性的情况。
如果我们希望提高查全率，尽可能地让所有有可能是恶性肿瘤的病人都得到进一步地检查、诊断，我们可以使用比 0.5 更小的阀值，如 0.3。
将不同阀值情况下，查全率与查准率的关系绘制成图表，曲线的形状根据数
据的不同而不同：

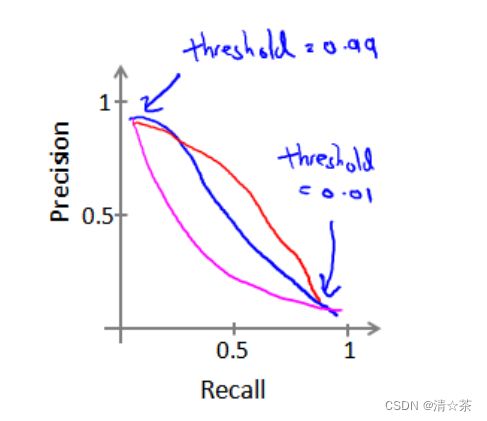
我们希望有一个帮助我们选择这个阀值的方法。一种方法是计算 F1 值（F1 Score），其计算公式为：

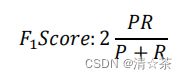
选择使得 F1 值最高的阀值。
吴恩达在机器学习中讨论了查准率（precision）和查全率（recall）之间的权衡。查准率和查全率是评估分类模型性能的两个重要指标，它们之间存在一种权衡关系。

查准率是指被正确分类的正样本占所有被分类为正样本的样本的比例。它衡量了模型在预测为正样本时的准确性。查准率高表示模型在预测为正样本时较少出现假阳性（将负样本错误地预测为正样本）的情况。

查全率是指被正确分类的正样本占所有实际正样本的比例。它衡量了模型对于实际正样本的覆盖程度。查全率高表示模型能够更好地捕捉到实际正样本，较少出现假阴性（将正样本错误地预测为负样本）的情况。
在实际应用中，我们往往需要根据具体的需求和场景来权衡查准率和查全率。如果我们更关注模型的准确性，希望尽量避免假阳性，那么我们会更注重查准率，即提高模型的准确性，即便牺牲一定的查全率。

相反，如果我们更关注模型对于实际正例的覆盖程度，希望尽量避免假阴性，那么我们会更注重查全率，即提高模型的敏感性，即便牺牲一定的查准率。
在不同的应用中，我们可能需要根据具体情况进行权衡。例如，在医疗诊断中，我们可能更关注查准率，确保尽量减少误诊的风险；而在垃圾邮件过滤中，我们可能更关注查全率，确保尽量捕捉到所有的垃圾邮件。

5.机器学习的数据

通过机器学习算法来区分常见的易混淆的单词，他们尝试了许多种不同的算法，并发现数据量非常大时，这些不同类型的算法效果都很好。
比如，在这样的句子中：早餐我吃了__个鸡蛋(to,two,too)，在这个例子中，“早餐我吃了 2 个鸡蛋”，这是一个易混淆的单词的例子。于是他们把诸如这样的机器学习问题，当做一类监督学习问题，并尝试将其分类，什么样的词，在一个英文句子特定的位置，才是合适的。使用了一个方差，用于逻辑回归上的一个方差，被称作"感知器"(perceptron)。

什么时候我们会希望获得更多数据，而非修改算法。他们所做的就是改变了训练数据集的大小，并尝试将这些学习算法用于不同大小的训练数据集中，这就是他们得到的结果：

这些趋势非常明显，首先大部分算法，都具有相似的性能，其次，随着训练数据集的增大，在横轴上代表以百万为单位的训练集大小，从 0.1 个百万到 1000 百万，也就是到了 10亿规模的训练集的样本，这些算法的性能也都对应地增强了。
那么让我们来看一看，大量的数据是有帮助的情况。假设特征值有足够的信息来预测值，假设我们使用一种需要大量参数的学习算法，比如有很多特征的逻辑回归或线性回归，或者用带有许多隐藏单元的神经网络，那又是另外一种带有很多参数的学习算法，这些都是非常强大的学习算法，它们有很多参数，这些参数可以拟合非常复杂的函数，因此我要调用这些，我将把这些算法想象成低偏差算法，因为我们能够拟合非常复杂的函数，而且因为我
们有非常强大的学习算法，这些学习算法能够拟合非常复杂的函数。很有可能，如果我们用这些数据运行这些算法，这种算法能很好地拟合训练集，因此，训练误差就会很低了。
现在假设我们使用了非常非常大的训练集，在这种情况下，尽管我们希望有很多参数，但是如果训练集比参数的数量还大，甚至是更多，那么这些算法就不太可能会过度拟合。也就是说训练误差有希望接近测试误差。
另一种考虑这个问题的角度是为了有一个高性能的学习算法，我们希望它不要有高的偏差和方差。
因此偏差问题，我们将通过确保有一个具有很多参数的学习算法来解决，以便我们能够得到一个较低偏差的算法，并且通过用非常大的训练集来保证。

特征值有足够的信息量，且我们有一类很好的函数，这是为什么能保证低误差的关键所在。它有大量的训练数据集，这能保证得到更多的方差值，
因此这给我们提出了一些可能的条件，如果你有大量的数据，而且你训练了一种带有很多参数的学习算法，那么这将会是一个很好的方式，来提供一个高性能的学习算法。