基于MWORKS.Sysplorer的油气混合作动筒建模与仿真应用

作为常见的线性传动装置，液压作动筒因其高功率密度和传动平稳、可控性好等特点而被广泛应用于各领域。常规的液压作动筒以油液为介质传递动力，其原理结构如图1所示。液压油从无杆腔进入，推动作动筒活塞伸出；或从有杆腔流入，推动作动筒活塞缩回。

图1 常规液压作动筒原理示意图

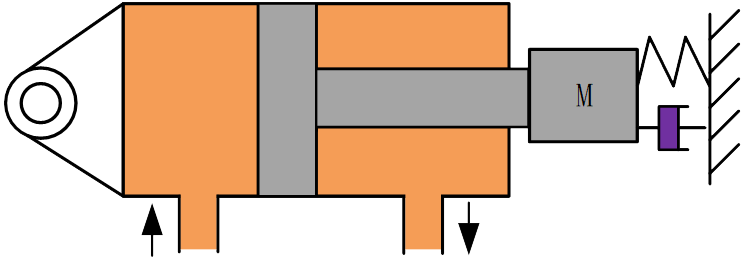
在一些场景下，出于可靠性要求，作动筒需要在如图2所示两种工况下工作：第一种工况，同常规液压作动筒一样，液压源提供动力，油液传递动力；第二种工况，当液压系统发生故障时，油路被断开，由气源提供动力，惰性气体传递动力，完成作动筒的单向伸出动作以保证整个系统的安全运行。本文称该种作动筒为油气混合作动筒。

图2 油气混合作动筒原理示意图

需要区分的是，存在一种液压油和气体作用在不同腔体的作动筒与本文所述的油气混合作动筒功能相似，其结构如图3所示，该构型作动筒可在MWORKS.Sysplorer中使用同元商业模型库TYHydraulicComponents和TYPneumaticComponents进行拖拽式建模，此处不再赘述。

因此特别强调本文所述的油气混合作动筒为油气共用同一腔体。油气混合作动筒建模需进行同腔体的油气切换计算，涉及切换条件判断和状态变量重置等问题，具有一定的复杂性。

图3 油气异腔作动筒原理示意图

本文基于MWORKS.Sysplorer，采用Modelica语言构建油气混合作动筒模型。

在进行油气混合作动筒建模之前，首先明晰常规液压作动筒建模机理。

常规液压作动筒的模型可以等效为两个液压腔体和一个质量块，这是由其机构决定的。液压作动的本质就是通过控制作动筒左右两个腔体的油液来实现对活塞的力/速度/位移控制。

从物理模型角度，活塞可视为一个质量块，描述质量块的运动只需要描述它的受力情况。那么作动筒中活塞的受力来自何处？显然，在作动筒内部受力主要是两个液压腔体的压强作用在活塞面积上产生的液压力。

那么再继续追问，液压腔体的压强如何产生？以作动筒无杆腔为例，观察图1，流入作动筒无杆腔的油液想要推动活塞向右运动，但是遇到活塞和负载的“抵抗”，在推动活塞运动之前无杆腔体积不变。随着油液不断流入无杆腔，由于流体压缩性，该腔压强不断上升，直至无杆腔压强作用在活塞上产生的力能够克服负载和摩擦等阻力，推动活塞运动。也就是说，在密闭容积内流体受压时压强相应增加，压强作用在活塞产生力，力作用下活塞运动。

上面定性的分析了液压作动筒的模型机理，那么接下来将定量的用数学语言描述模型。

首先分析力作用下的活塞运动。假设已知无杆腔和有杆腔的压强分别为和，把活塞和负载质量视为一个质量块，那么根据牛顿运动定律，有以下方程：

（1）

其中，为活塞的总质量，为活塞所受的外部负载力，为活塞所受阻尼力和摩擦力，为作动筒活塞无杆腔面积，为作动筒活塞无杆腔面积，为作动筒活塞位移。

从上述方程，可以根据两腔体压力计算活塞的加速度，进而由积分计算速度和位移。那么如何计算两个腔体的压力呢？

前面已经讲过，在活塞被推动之前，流体不断流入容腔，由于流体的压缩性产生压力。在活塞实际运动的过程中，流入腔体的流量分为三部分：一部分为补充活塞运动产生的流量；一部分为补充流体压缩引起的流量；还有一部分为泄漏流量。作动筒两腔的流量和的方程如下所示：

（2）

（3）

其中，为作动筒无杆腔容积，为作动筒有杆腔容积，为作动筒内泄漏系数，为液压油体积弹性模量。

因此，描述作动筒的运动状态仅需要三个方程。力平衡方程(1)描述活塞的受力运动，给出两腔压强和与活塞位移之间的数学关系；流量连续性方程(2)和(3)描述液压腔体的状态，给出腔体压强和输入流量之间的数学关系。

油气混合作动筒与常规作动筒的最大区别在于油液作动到气体作动的切换，即某一时刻液压系统故障，液压源切换为气压源，由气压源推动活塞完成伸出动作。首先考虑气腔的建模。

3.1 气腔建模

不妨假设已经完成切换，油气混合作动筒左端为气腔，右端为油腔，那么活塞的运动方程与(1)相同。

（4）

其中，为无杆腔气体压强。那么仅需再计算出气体腔体压力，即可完成左腔为气腔右腔为油腔的油气混合作动筒的数学描述。

描述气体压力的方程如下所示：

（5）

其中，为无杆腔体积；为气体质量；为气体常数，由介质类型确定；为气体温度。的计算可由输入到该腔的质量流量积分得到，有如下方程：

（6）

那么仅剩温度需要计算，可由如下方程计算：

（7）

其中，为比热比，和分别为定压比热容和定容比热容；在气体流入时为环境温度；为腔体体积变化速率，为活塞速度。

3.2 油气混合作动筒建模

油气混合模型需要考虑液压工况时油腔的计算向气压工况时气腔的计算切换。首先需要明确模型何时开启计算切换。实际物理系统中是由外部的气压或液压控制元件进行主动的切换，作动筒仅需被动接受动力源即可。那么在模型中我们如何处理，让油气混合作动筒模型知道什么时候开始进行气压计算呢？这就涉及到判断条件的问题。

不妨先设置一个布尔类型标志变量，默认值为0，表示此时为液压工况状态；切换为气压工况状态时通过判断条件令，进而计算气压工况状态下的变量。刚刚已经讲述，在实际物理系统中，作动筒被动接受动力源。那么在油气混合作动筒模型中，可以从物理接口的流量信号来判断切换与否。当气体流量大于设定阈值后，油气混合作动筒模型由液压工况切换到气压工况，如下所示：

（8）

在状态切换的同时，也要对状态变量进行重置，这点在后面讲述。

无论是在液压工况下还是在气压工况下，其本质均为腔体内的压强作用在无杆腔活塞面产生作用力。因此，首先区分两个状态下的力，不妨设气压工况时腔体内的气体作用力为，液压工况时腔体内的液压作用力为，重新构建运动方程如下：

（9）

液压力和气压力计算如下所示：

（10）

观察上式，我们想要使模型在液压工况时，仅计算；在气压工况时，仅计算。那也就是说，要设法令液压工况时；令气压工况时。

在液压工况下，需要计算两个状态变量液压腔体压力和气腔温度，

(11)

由式（5）可知，令气体质量为0，那么气体压强也为0，进而在液压工况时气压力，仅进行液压相关变量的计算。

气压工况下，也需要计算两个状态变量液压腔体压力和气腔温度。因为在Modelica语言中，if产生的选择分支的方程数量必须相等。

(12)

到这里，基本的建模已经完成。不过细心的你可能会发现，仍然残留有一些小问题。比如前文中提到令气体质量为0，但是在式（12）中为分母；在式（12）中仅令的微分为0，并没有将它本身重置为0。因此在状态切换的同时，应当将重置为0，将重置为一较小值以进行计算。那么如何重置这些状态变量的值呢？

复杂的建模中经常要面临状态变量的数值重置和微分方程切换。在Modelica语言中可以使用reinit对状态变量数值进行重置，大大方便了在状态变量微分方程切换场合时的建模与仿真。

4.1 模型验证

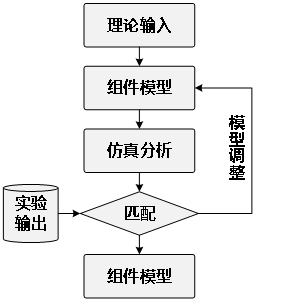
基于上述方程对油气混合作动筒进行建模，根据相关实验数据，按照如图4所示的组件模型验证流程对油气混合作动筒模型进行验证迭代，直至模型输出符合理论及物理规律。

图4 组件模型验证流程

经与实验数据对比验证，本文所构建的油气混合作动筒模型输出符合理论及实际物理规律，数值仿真结果与实验数据匹配良好，模型所计算的液压压力平均误差为3.3%，气压压力平均误差为5.6%，活塞位移平均误差为1.2%。基于本模型进行下述应用场景验证。

4.2 典型应用场景仿真

建立如下图所示的模型对油气混合作动筒模型进行典型应用场景仿真。

图5 油气混合作动筒典型应用场景仿真模型图

应用场景如下：0-2秒进行液压作动，活塞在油液作用下伸出。在2秒时，活塞运动到某位置，液压系统故障，该腔油液全被放掉油压为0；模型开始进行气压作动计算，活塞在之前的位置上被气体继续推动完成伸出动作。

仿真工况如下：在0-2秒给定油液流量源0.2kg/s的恒定流量，油气混合作动筒模型能仿真液压传动下的伸出动作；假设在仿真的第2秒液压系统发生故障，气体流量源开始供气，流量恒定为0.01kg/s。

​

所得到的仿真结果如下：

图6 油气混合作动筒活塞位移曲线图

图7 油气混合作动筒活塞速度曲线图

图8 油气混合作动筒左腔液压压强和气压压强曲线图

图9 油气混合作动筒左腔气体温度曲线图

图10 油气混合作动筒液压气压标记曲线图

由仿真曲线可知，油气混合作动筒模型能准确的描述切换前后的液压和气压状态，处理切换过程中的状态变量的微分方程切换和数值重置等情况。

本文从常规液压作动筒的建模出发，主要介绍了一种具备不同工况油气同腔切换特点的油气混合作动筒建模方法。文中给出了油气混合作动筒的应用场景并分析了其物理行为特点，针对该种作动筒油气同腔切换的特点提出了一种涉及状态变量微分方程切换和数值重置的油气混合作动筒建模方法。基于MWORKS.Sysplorer实现了油气混合作动筒的建模并对模型进行了验证。

MWORKS.Sysplorer为机电液系统提供广泛且深入的建模仿真平台支持。如果您需要文中提及的油气混合作动筒的主要代码，请回复评论并留下您的邮箱，我们会尽快发送给您！

我们还将不定期推出更多的技术文章，介绍MWORKS.Sysplorer的使用攻略和相关专业学科原理的应用等信息，欢迎继续关注我们的后续推送！