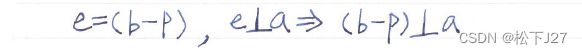线性代数 --- 投影Projection 一（投影向量p）

线性代数中的投影

        之前看过Gilbert strang老爷爷在MIT主讲的线性代数视频，令我印象最深的，就是他讲过的一堂关于投影的课。倒不是这堂课的内容本身有多么的吸引我，反倒是他在这堂课中所说的一句话，时至今日都另我印象深刻。

他的原话是：“我要让这堂课不朽（immortal）”

        当时，我看了以后，感觉整个人都被震住了。细细想来，一个老师，居然在他的课上，一开始就说，要让他的这堂客不朽。这得需要何等的自信，这得多么热爱自己所教的这门课啊。这句话一直激励着我，一定要把线性代数学好，尤其是要把线性代数中的投影学好。1，是为了证明自己，当初上学的时候，线性代数学的不好，并不是因为自己笨，尤其是不是因为自己比别的同学笨。2，是只有真正把线性代数学好了，才能真正的理解这门，被Gilbert strang称之为不朽的课程 --- 投影。

        言归正传，我自认为在学习投影的时候，花了很多时间和精力，也走了很多弯路。现在我就把我对投影的理解梳理出来，分享给有需要的人，同时，更是对我自己学习的一个总结和梳理。（---松下J27）

---

如何计算向量的投影

        在线性代数投影的学习中，有两个非常重要概念，或者说我们一直在试图回答两个问题：（以二维空间为例）

1，对于一个任意向量b而言，他在另一个向量上的投影是什么？尤其是，他在x-y轴上的投影是什么？

这个问题的答案，就是要找到投影向量p(小写的p)。例如，向量b=[1,5]，在x轴[x,0]上的投影为p_x=[1,0]，在y轴[0,y]上的投影为p_y=[0，5]。

2，有没有一个矩阵P，能把任意向量都投影到指定的向量上去？例如，矩阵P[1 0;0 0]可以把二维空间中的任意向量都投影到x轴上去

而这个问题的答案，是要找到一种线性变换或者说是投影矩阵P(大写的P)，他可以把任何矩阵都投影到指定的向量上去。

---

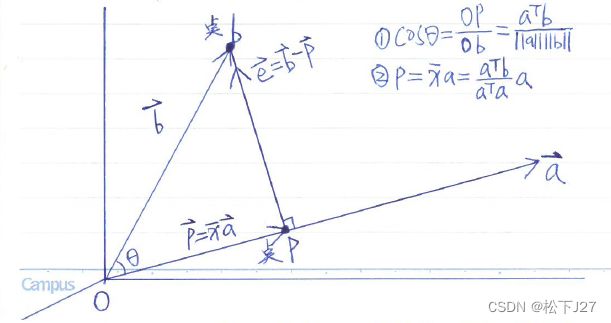
向量b在向量a上的投影向量p

        现在，我们先把目光聚焦在计算投影向量p上：也就是在二维空间中，如何求出一个向量在另一个向量上的投影？

        做向量b到向量a所在直线的垂线，垂于点p，得到b在a上的投影Op，即投影向量p(记为英文字母小写p)。

其中：

（1）向量a所在直线上的垂点p，是向量b的端点b在直线a上的投影点。

（2）向量p是向量b在直线a上的投影向量。向量p与向量a的方向相同，大小是a的某一倍数(为了方便后续的描述和学习，我们暂且称之为投影系数)，读作x hat。

        记作：

（3）点p到点b的连线垂直于Oa,它是点b到Oa的最短距离。

        

        前面说过，投影向量p与a的方向相同，但长度不同。且，向量p的长度与a之间满足一定的比例。也就是说，只要求出了投影系数，就相当于求出了投影向量p: 

p=a

现在，我们分别通过两种方法计算投影系数：

1，利用直角三角形中夹角的余弦。（适用于二维和三维空间）

2，利用正交向量的内积为0，也就是根据投影向量p与垂线e相互垂直。（适用于更高维空间）

---

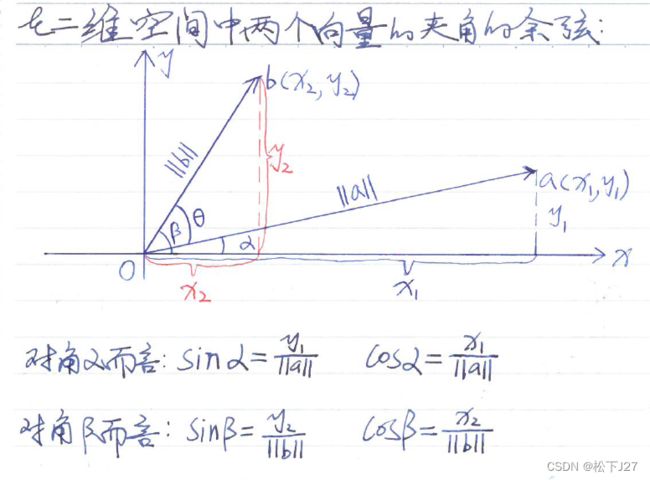
方法1，两个向量夹角的余弦：

        先简单的回顾一下，需要用到的三角函数和线性代数的基础知识，以及三角函数中的一些定理用线性代数的语言是如何描述的。

向量的内积/点积：

向量的长度: 

 用向量的长度来表示直角三角形的边长：

用向量的长度与向量的内积来表示夹角的余弦：

得到α和β的正弦和余弦后，根据余弦的和差公式，我们求得了用两个向量的内积与两个向量的长度表示的角θ的余弦:

（请注意上图中用a,b的内积表示x1x2+y1y2的部分）

        

        现在我们再回到之前所画的投影图中，点b和他在a上的投影---点p，再加上原点o，共同构成了直角三角形。Op的长度是Oa的某一倍数，即投影系数，是一个常数。

        首先，在直角三角形中，利用角θ的余弦等于领边Op比斜边Ob，得到式1：

         其次，向量a与向量b的夹角为θ，根据之前推导出来的两个向量的夹角的余弦公式，得到式2：（这一结论也可以通过三角函数中的余弦定理求得）

联合式1和式2得到：

 小结：

        如果只在二维和三维空间中讨论向量的投影，都可以用三角函数中的余弦的和差公式（或：余弦定理）等三角函数的知识来计算。但是，如果上升到n维，也就是的空间中，角度/夹角这个几何术语的定义本身都不确定了/或者说不存在/不适用了，这样一来，我们在二维空间中利用三角函数的知识计算得来的投影系数在高维空间(n>3)中就不一定适用了。

---

方法2，正交向量的内积为0：

        在本文的上一节所提到的方法1中，我们利用三角函数的知识，基于两个向量夹角的余弦求出了投影系数，继而求出了投影向量p。但之前的那种方法只适用于低维度的空间，这里我们要介绍一种适用于所有维度的计算投影系数的算法，即，两个相互垂直的向量，他们的内积为0。

        投影点p到向量b的端点b的连线---向量e=b-p，垂直于向量a。我们有：

         根据两个相互垂直的向量他们的内积为零，有：

        这样一来，我们就在不使用任何三角函数相关知识的情况下，计算出了和前面一样的投影系数。同时，也把投影向量的计算方法推广到了更高的维度。

最后：

 （全文完）

作者 --- 松下J27

参考文献（鸣谢）：

1，《Introduction to Linear Algebra》,5th Edition - Gilbert Strang

 2，线性代数及其应用，侯自新，南开大学出版社，1990.

古诗词赏析：

《读孟尝君传》　　王安石（宋）

        世皆称孟尝君能得士，士以故归之，而卒赖其力以脱于虎豹之秦。嗟乎！孟尝君特鸡鸣狗盗之雄耳，岂足以言得士？不然，擅齐之强，得一士焉，宜可以南面而制秦，尚何取鸡鸣狗盗之力哉？夫鸡鸣狗盗之出其门，此士之所以不至也。

 

（配图与本文无关）

重要的事情说三遍：

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27