电子技术——MOS管的CV特性

电子技术——MOS管的CV特性

MOS管是一种压控晶体管，本节我们学习MOS管的CV特性，即电压-电流特性。MOS管的特性曲线有两种，分别是伏安特性和传导特性。

$i_D-v_{DS}$ 特性曲线

为了测量MOS管的 $i_D-v_{DS}$ 曲线，我们使用下面的电路：

由上图可知，我们固定栅极电压 $v_{GS}$ 然后调节源极-漏极电压 $v_{DS}$ 来观察漏极电流 $i_D$ 的变化。通过这样的方法，我们就可以绘制出MOS管的CV特性曲线如下图：

图中显示了三个区域，分别是 截止区域 饱和区域 三极管区 。其中截止区域和三极管区作用于开关电路。

换句话说，如果MOS管用作于放大器，他必须处在饱和区。

图中展现了两条曲线，一种是在 $v_{GS}<V_{tn}$ 情况下测量的，此时MOS管永远工作在截止区，因为栅极没有足够大于阈值电压的电压来创建沟道，因此漏极电流恒为零。另一种是在 $v_{GS}=V_{tn}+v_{OV}$ 下测量，此时MOS管打开，可能处在三极管区，也可能处在饱和区。

三极管区和饱和区的边界即是 $v_{DS}$ 和 $v_{OV}$ 之间的大小关系，若想MOS管工作在饱和区，那么必须使得 $v_{DS}>v_G-V_{tn}$ 。

$i_D-v_{GS}$ 特性曲线

由上节的知识，我们知道，当MOS管工作在饱和区的时候，此时 $i_D$ 与 $v_{DS}$ 无关，只与 $v_{OV}$ 有关，关系是：

$$i_D=\frac{1}{2}{k}_n^{\prime }(\frac{W}{L})v_{OV}^2$$

在不同 $v_{OV}$ 测量得到的曲线如下：

此时，我们假设MOS管工作在饱和区（漏极电压足够大），那么 $i_D-v_{GS}$ 特性曲线应该是如下的二次曲线：

MOS管的有限内阻

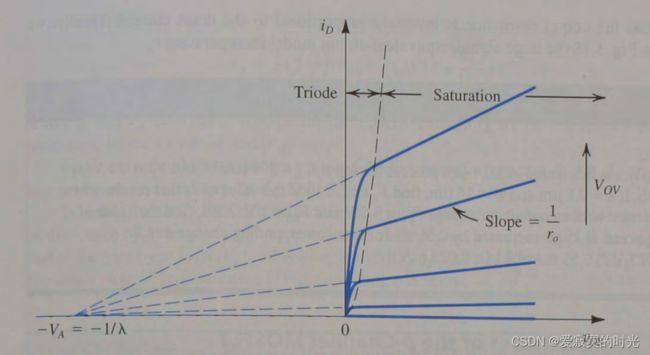
观察伏安特性曲线，MOS管在饱和区显示出内阻无限大的特性（理想电流源），但是世上没有内阻无限大的电路，实际上MOS管一定是存在内阻的，改变 $v_{DS}$ 电压产生的一个最大的效应就是会改变MOS管沟道的长度，如图所示：

图中沟道减小的那一段距离 $\Delta L$ 就是由电压 $v_{DS}-v_{OV}$ 造成的线性变化，进而影响 $i_D$ 电流，这个效应称为 沟道长度调制效应 。

我们通过一个因子 $\lambda$ 来描述这个变化， $\lambda$ 参数是MOS管本身工艺和原始长度 $L$ 决定的：

$$i_D=\frac{1}{2}{k}_n^{\prime }(\frac{W}{L})v_{OV}^2(1+\lambda v_{DS})$$

我们发现，新的曲线的延长线都交于一点 $-V_A=-\frac{1}{\lambda }$ ，即 $V_A=\frac{1}{\lambda }$ 具有电压量纲。我们可以分离 $L$ 变量：

$$V_A=V_A^{\prime }L$$

此时 $V_A^{\prime }$ 只和MOS管本身工艺有关，这个电压也称为厄尔利电压。

引入沟道长度调制效应之后，我们发现，MOS管不再显示出无限内阻特性，而是等效于一个有内阻的电流源：

这个内阻我们记为 $r_o$ 定义为：

$$r_o\equiv [\frac{\partial i_D}{\partial v_{DS}}{]}_{v_{GS}=const}^{-1}$$

求导可的：

$$r_o=[\lambda \frac{k_n^{\prime }}{2}\frac{W}{L}(V_{GS}-V_{tn}){]}^{-1}$$

带入饱和电流公式：

$$r_o=\frac{1}{\lambda I_D}=\frac{V_A}{I_D}$$

其中 $I_D$ 是之前无沟道长度调制效应时的饱和电流，由此可见，内阻和漏极电流成反比。