电子技术——MOS管的小信号模型
电子技术——MOS管的小信号模型
在上一节，我们已经学习过了MOS管的基本线性放大原理，本节我们继续深入MOS管的小信号放大，建立MOS管的小信号模型。
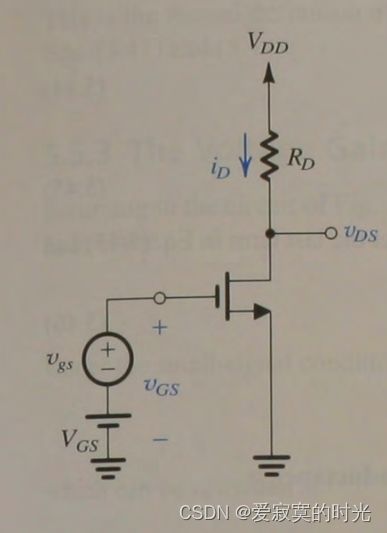
我们本节继续使用上节的电路，如下图所示：
DC偏置点
根据上节的知识，我们知道漏极DC电流为：
I D = 1 2 k n V O V 2 I_D = \frac{1}{2} k_n V_{OV}^2 ID=21knVOV2
在这里我们忽略MOS管的沟道长度调制效应（ λ = 0 \lambda = 0 λ=0 ）。
输出DC电压为 V D S = V D D − R D I D V_{DS} = V_{DD}-R_DI_D VDS=VDD−RDID 。
为了保证MOS管工作在饱和区，必须使得 V D S > V O V V_{DS} > V_{OV} VDS>VOV 。因为输出信号直接叠加在 V D S V_{DS} VDS 上，漏极电压必须留出足够的余量，使得MOS工作在饱和区。
漏极的信号电流
接下来，我们考虑叠加 v g s v_{gs} vgs ，因此 v G S = V G S + v g s v_{GS} = V_{GS} + v_{gs} vGS=VGS+vgs ，这导出漏极的瞬时电流值：
i D = 1 2 k n ( V G S + v g s − V t ) 2 = 1 2 k n ( V G S − V t ) 2 + k n ( V G S − V t ) v g s + 1 2 k n v g s 2 i_D = \frac{1}{2} k_n(V_{GS} + v_{gs} - V_t)^2 = \frac{1}{2} k_n(V_{GS}-V_t)^2 + k_n(V_{GS}-V_t)v_{gs} + \frac{1}{2} k_nv_{gs}^2 iD=21kn(VGS+vgs−Vt)2=21kn(VGS−Vt)2+kn(VGS−Vt)vgs+21knvgs2
式子中的第一项是我们的DC偏置电流 I D I_D ID ，第二项正比于 v g s v_{gs} vgs ，第三项正比于 v g s 2 v_{gs}^2 vgs2 。第三项是我们不希望的信号，因为这引入了非线性的信号失真。为了解决这一点，我们必须保证我们的信号 v g s v_{gs} vgs 足够小，以至于：
1 2 k n v g s 2 ≪ k n ( V G S − V t ) v g s \frac{1}{2} k_n v_{gs}^2 \ll k_n(V_{GS} - V_t)v_{gs} 21knvgs2≪kn(VGS−Vt)vgs
或者说是：
v g s ≪ 2 V O V v_{gs} \ll 2V_{OV} vgs≪2VOV
如果上式满足，那么我们就可以忽略最后一项，即：
i D ≃ I D + i d i_D \simeq I_D+ i_d iD≃ID+id
也就是说，漏极电流的顺时值可以看做是DC电流上叠一个信号电流，在这里信号电流
i d = k n ( V G S − V t ) v g s i_d = k_n (V_{GS}-V_t)v_{gs} id=kn(VGS−Vt)vgs
信号量 v g s v_{gs} vgs 和 i d i_d id 之间有互导关系，我们定义互导系数为 g m g_m gm ：
g m ≡ i d v g s = k n ( V G S − V t ) = k n V O V g_m \equiv \frac{i_d}{v_{gs}} = k_n(V_{GS}-V_t) = k_nV_{OV} gm≡vgsid=kn(VGS−Vt)=knVOV
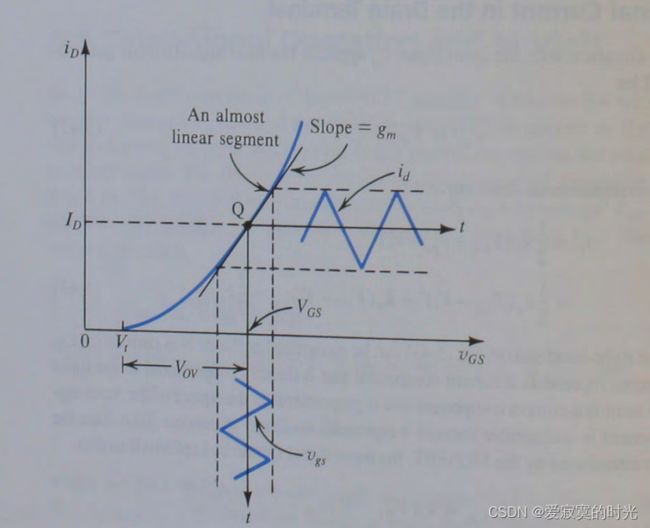
互导系数的意义如下图，下图是MOS管的互导特性曲线图，上叠信号作用于Q点， g m g_m gm 正好是Q点处的斜率。
g m ≡ ∂ i D ∂ v G S ∣ v G S = V G S g_m \equiv \frac{\partial i_D}{\partial v_{GS}} |_{v_{GS}=V_{GS}} gm≡∂vGS∂iD∣vGS=VGS
最终 i d = g m v g s i_d = g_m v_{gs} id=gmvgs 。
信号电压增益
讨论完小信号模型中的信号电压和信号电流之间的关系，现在让我们计算信号电压的增益。根据上节的放大器模型：
v D S = V D D − R D i D v_{DS} = V_{DD} - R_Di_D vDS=VDD−RDiD
使用小信号电流 i D = I D + i d i_D = I_D+ i_d iD=ID+id 我们有：
v D S = V D S − R D i d v_{DS} = V_{DS} - R_Di_d vDS=VDS−RDid
我们将后项定义为信号的输出电压 v d s = − R D i d = − g m v g s R D v_{ds} = -R_Di_d = -g_m v_{gs} R_D vds=−RDid=−gmvgsRD 。
则信号的电压增益为：
A v ≡ v d s v g s = − g m R D = − k n V O V R D A_v \equiv \frac{v_{ds}}{v_{gs}} = -g_m R_D = -k_nV_{OV}R_D Av≡vgsvds=−gmRD=−knVOVRD
这个式子说明电压增益为负值，输入信号电压和输出信号电压直接相差了180度。最终我们发现信号电压增益和我们在上一节得到的瞬时电压增益一样。
分离DC分析和小信号分析
通过上面的瞬时电流电压值的式子，我们发现，只要我们满足下面的条件：
- MOS管Q点工作在饱和区，并且瞬时也工作在饱和区。
- 信号满足小信号条件，即 v g s ≪ 2 V O V v_{gs} \ll 2V_{OV} vgs≪2VOV 。
那么我们可以分离DC分析和小信号分析，我们可以首先进行DC分析，计算Q点坐标，然后根据Q点坐标确定互导系数，之后进行小信号分析。
小信号等价电路模型
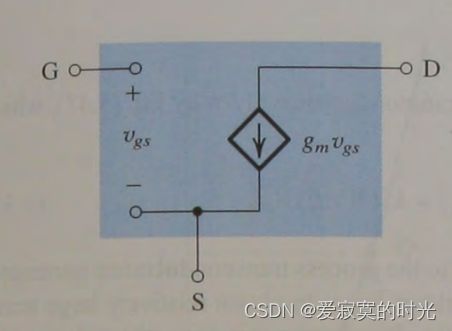
从信号的角度考虑，MOS管相当于一个压控流源，从栅极输入电压 v g s v_{gs} vgs 那就会在漏极输出一个电流 g m v g s g_m v_{gs} gmvgs ，输入阻抗无穷大，输出阻抗理论上也无穷大，放在一起得到我们的等价电路模型如下图：
我们称这个模型为 小信号模型 和对应的 小信号等价电路 。
对于电路中剩下的部分，即DC部分，我们将DC部分的值置为0，即将DC电压源短路DC电流源断路。
但是这个模型有一个缺点就是我们默认假设漏极电流与漏极电压无关，可是根据前面的小节的学习我们知道，MOS管的输出阻抗并不是理想无穷大，而是为：
r o = ∣ V A ∣ I D r_o = \frac{|V_A|}{I_D} ro=ID∣VA∣
这里 V A = 1 λ V_A = \frac{1}{\lambda} VA=λ1 ，是与MOS本身有关的参数， I D I_D ID 是不考虑调制效应时候的漏极DC电流。这个电阻 r o r_o ro 同样会作用于信号上，因此我们在我们电路模型上引入这个电阻：
回到我们电路模型中，我们发现，引入电阻 r o r_o ro 后电压增益变为：
A v = − g m ( R D ∣ ∣ r o ) A_v = -g_m (R_D || r_o) Av=−gm(RD∣∣ro)
因此，这个有限阻抗的MOS管降低了电压增益。
互导系数 g m g_m gm
我们继续深入研究一下小信号模型中的互导系数 g m g_m gm ，我们将其展开为：
g m = k n ′ ( W / L ) ( V G S − V t ) = k n ′ ( W / L ) V O V g_m = k_n' (W/L) (V_{GS} - V_t) = k_n' (W/L) V_{OV} gm=kn′(W/L)(VGS−Vt)=kn′(W/L)VOV
我们发现互导系数正比于常量 k n ′ k_n' kn′ 和 MOS管的宽长比 W / L W/L W/L 因此要获得更大的电压增益，MOS管必须做的又短又宽。 g m g_m gm 还正比于 V O V V_{OV} VOV ，但是上节我们知道，如果增大 V O V V_{OV} VOV 的值，那么将会减小信号的最大允许幅值。
另外一个有用的式子是：
g m = 2 k n ′ W / L I D g_m = \sqrt{2k_n'} \sqrt{W/L} \sqrt{I_D} gm=2kn′W/LID
这个表达式说明两件事情：
- 对于给定的MOS管， g m g_m gm 只正比于 I D \sqrt{I_D} ID 。
- 对于给定的偏置电流， g m g_m gm 只正比于 W / L \sqrt{W/L} W/L 。
还有另外一种表达形式：
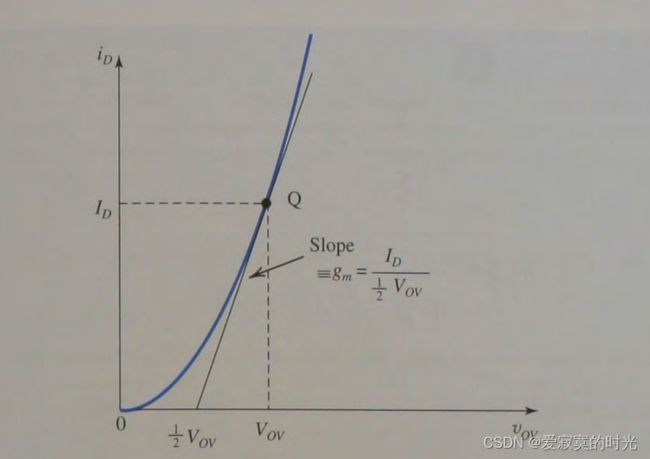
g m = 2 I D V O V g_m = \frac{2I_D}{V_{OV}} gm=VOV2ID
为了提供MOS管的尺寸无关性设计，一般工程师使用下面的互导特性曲线图像来确定为了达到预期 g m g_m gm 而需要的正确偏置点。
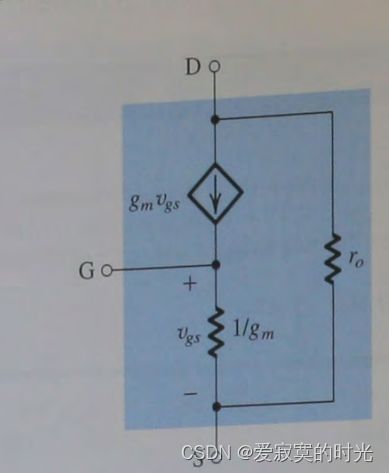
等效 T 模型
除了上面我们建立的理想压控流源模型外，我们还有另外一个模型，称为 T 模型，如下图：
图中(a)是我们学习过的理想压控流源模型，在(b)中我们复制一份流源而不会影响整个电路。我们创建一个新的节点，标记为X，连接到MOS管的栅极，如图©。观察栅极电流不会发生变化，也就是说依旧保持电流为零，并且也不会改变MOS管的端特性。我们发现输入电压 v g s v_{gs} vgs 直接作用于受控流源 g m v g s g_m v_{gs} gmvgs 两端，因此，此时可以使用一颗电阻来替换电流源，那么电路的属性依然不会发生改变。这颗电阻的阻值应该为 1 g m \frac{1}{g_m} gm1 ，如图(d)。
这个模型被称为 T 模型 ，注意虽然栅极直接和电路相连，但是栅极的输入阻抗依旧是无穷大。
注意到上面电路我们没有引入 r o r_o ro ，如果需要，仍然可以在DS两端引入电阻 r o r_o ro 如下图：
为了区分和之前的模型，我们称之前的理想压控流源模型为混合 π \pi π 模型。