时域信号中的噪声特性研究:平稳与非平稳噪声的比较分析
平稳噪声(Stationary Noise)和非平稳噪声(Non-stationary Noise)是信号处理和统计学中常用的术语,用于描述噪声信号的特性。
1. 平稳噪声
定义: 平稳噪声是指其统计特性在时间上保持不变的噪声。具体来说,平稳噪声的均值和方差在时间的任何时刻都是常数。
性质:
- 平稳噪声的均值对于时间是常数。
- 方差对于时间是常数。
- 自相关函数(autocorrelation function)只依赖于时间差,而不依赖于时间本身。
2. 非平稳噪声(Non-stationary Noise):
定义: 非平稳噪声是指其统计特性在时间上变化的噪声。换句话说,非平稳噪声的均值、方差或自相关函数在时间上可能发生变化。
性质:
- 非平稳噪声的均值、方差或自相关函数可能随时间发生变化。
- 经典的例子是随时间变化的趋势或周期性的噪声。
在实际应用中,平稳噪声通常更容易处理,因为它的统计性质在整个时间范围内保持不变。非平稳噪声可能需要更复杂的方法来进行建模和处理,因为其统计性质可能随时间变化。
3. MATLAB对比分析
% 生成平稳噪声信号
rng(42); % 设置随机数生成器的种子以确保结果可重现
t = 0:0.01:1; % 时间范围
mean_value = 0;
std_dev = 1;
stationary_noise = mean_value + std_dev * randn(size(t));
% 绘制平稳噪声信号和自相关函数
figure;
subplot(2,1,1);
plot(t, stationary_noise);
title('Stationary Noise Signal');
xlabel('Time');
ylabel('Amplitude');
subplot(2,1,2);
autocorr(stationary_noise);
title('Autocorrelation of Stationary Noise');
这个例子生成了一个平稳噪声信号,然后绘制了信号的时域图和自相关函数。在平稳噪声中,自相关函数是一个在时间差上几乎不变的常数。
% 生成非平稳噪声信号
t = 0:0.01:1; % 时间范围
mean_values = sin(2*pi*t); % 随时间变化的均值
std_dev = 1;
non_stationary_noise = mean_values + std_dev * randn(size(t));
% 绘制非平稳噪声信号和自相关函数
figure;
subplot(2,1,1);
plot(t, non_stationary_noise);
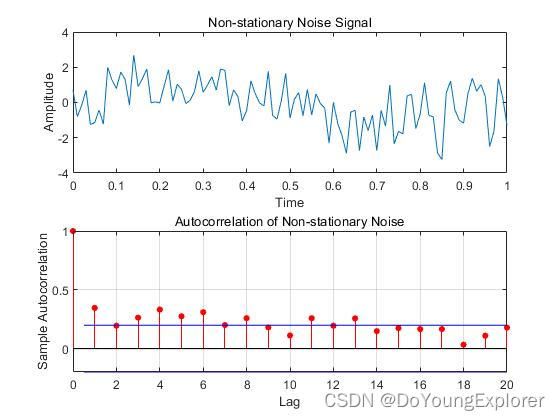
title('Non-stationary Noise Signal');
xlabel('Time');
ylabel('Amplitude');
subplot(2,1,2);
autocorr(non_stationary_noise);
title('Autocorrelation of Non-stationary Noise');
这个例子生成了一个非平稳噪声信号,其均值随时间变化。在非平稳噪声中,自相关函数可能会随时间变化而变化。通过比较这两个例子,你可以观察到平稳噪声的统计性质在整个时间范围内基本保持不变,而非平稳噪声的统计性质可能随时间发生变化。
4. 自相关函数分析
下面我将解释一下如何理解自相关函数的图像:
自相关函数图解释:
- 横轴(X轴): 表示时间差(lag),即当前时刻与之前的时刻之间的时间间隔。
- 纵轴(Y轴): 表示信号在不同时间差下的相关性。
自相关函数图的解读:
- 峰值和谷值: 自相关函数图中的峰值表示信号在对应时间差下的相关性很高,而谷值表示相关性较低。
- 周期性: 如果信号是周期性的,你可能会观察到自相关函数在某个时间差上有明显的周期性峰值。
平稳和非平稳信号的对比:
- 平稳信号: 自相关函数在不同时间差上的形状基本相同,峰值和谷值保持稳定。
- 非平稳信号: 自相关函数在时间差上可能有明显的变化,峰值和谷值可能会随时间而变化。
在之前的MATLAB示例中,我使用 autocorr 函数绘制了平稳和非平稳噪声信号的自相关函数。你可以观察自相关函数图,以了解信号的周期性、稳定性以及不同时间点上的相关性。为进一步说明,进行如下仿真
% 生成一个示例信号
t = 0:0.01:1;
x = sin(2*pi*5*t) + 0.5*randn(size(t));
% 计算自相关函数
lags = -length(t)+1:length(t)-1;
autocorr_values = xcorr(x, 'coeff');
% 绘制原始信号
figure;
subplot(2, 1, 1);
plot(t, x);
title('Original Signal');
xlabel('Time');
ylabel('Amplitude');
grid on;
% 绘制自相关函数图
subplot(2, 1, 2);
stem(lags, autocorr_values);
title('Autocorrelation Function');
xlabel('Lag');
ylabel('Autocorrelation Coefficient');
grid on;
以下是对自相关函数图形的形象解释:
零时间差(Lag为0):
- 自相关函数在零时间差处的值总是1,因为在这个时刻信号与自身完全重合,相关性最高。
峰值和谷值:
- 自相关函数图上的峰值表示信号在对应的时间差上具有很高的相关性,而谷值表示相关性较低。
- 峰值和谷值的位置和高度提供了关于信号的周期性和变化的信息。
- 如果存在周期性,你可能会看到多个峰值,每个峰值对应于信号的一个周期。
周期性:
- 如果信号是周期性的,自相关函数图上会显示出明显的周期性峰值。
- 周期性的峰值可以帮助你确定信号的周期。
衰减:
- 随着时间差的增加,自相关函数的值可能会衰减。衰减的速度和形式提供了关于信号衰减和趋势的信息。
截尾:
- 在某些情况下,自相关函数可能会在一定的时间差后截尾,表示信号与自身的相关性随时间差的增加而减小。
"Lag" 是一个表示时间序列中两个数据点之间的时间差的术语。在自相关函数中,Lag 表示在计算自相关性时一个信号相对于另一个信号的滞后(时间延迟)。单位取决于你使用的时间单位。在你提供的 MATLAB 代码中,时间步长 0.01 表示每个数据点之间的时间间隔。因此,Lag 的单位是这个时间间隔。具体来说,在你的代码中,t = 0:0.01:1; 中,时间步长为 0.01,表示每个数据点之间相隔 0.01 单位的时间。因此,Lag 表示数据点之间的时间差,单位是这个时间步长。例如,如果 Lag 为 10,表示对应的两个数据点之间有 10 * 0.01 = 0.1 的时间间隔。在自相关函数图中,Lag 为 0 时表示信号与自身在同一时间点,Lag 的增加表示信号之间的时间差增加。通过观察自相关函数图,你可以了解信号在不同时间差上的相关性,以及信号的周期性、趋势等信息。