信息隐藏——第二章 伪随机数发生器

一、概述
真随机数序列的定义:
①能通过所有正确的随机性检验。
②序列的产生是不可预知的。
③在完全相同的操作条件下得到的序列是不重复的
在自然界中确实拥有作为随机数发生器能产生满足这样定义的现象与实例，我们将这样的随机数称为真随机数

在实际应用中 最普遍的算法模式是迭代：Xi + 1 = f( Ε, Xi)

结合真随机数的定义, 我们需要从以下几个方面重点解决伪随机数性能
的问题:
①序列能否在一定置信度条件下通过所有正确的随机性检验。
②序列能否按照要求服从一定的概率分布。
③在不知道 Xn 的情况下能否保证一定不知道 Xn + 1 。
④在怎样的种子和参数控制下才能使序列保持较长的周期且不退化。
⑤不同种子控制下的序列能否不重复且能否尽可能地不相关。

二、服从均匀分布的伪随机数
1.目前应用最为 广泛的均匀分布伪随 机数发生器就是线性 同余伪随机发生器LCG。LCG 的迭代描述公式为:xi + 1 = ( a xi + c) ( mod m)
2.小数开方伪随机数发生器的基本原理是基于以下定理:
推导出：若当某一 xi 是一个无理数时, 则其后由迭代产生的数都将是无理数, 那么该序列的每一个数显然可以保持较长的位数, 从而避免了序列的退化。在不限定取值位数的条件下, 该方法产生的序列周期 T→∞。

function randmtx = randU2( row, col, seed, k1, k2)
if nargin < 3
seed = 11;
end
m = 4 ;
seed2 = sqrt( seed) ;
while seed2 < 1
seed2 = seed2* 10 ;
end
n = round( seed2 /m) ;
x = ( 10^n) * seed2;
randmtx( 1, 1) = x - floor( x) ;
for i = 2∶row* col
temp = sqrt( abs( randmtx( 1, i-1) ) ) ;
while temp < 1
temp = temp* 10;
end
n = round( temp /m) ;
x = ( 10^n) * temp;
randmtx( 1, i) = ( x - floor( x) ) ;
end
randmtx = reshape( randmtx, row, col) ;
if nargin < 4
return
end
randmtx = randmtx* ( k2 - k1) + k1;

3.对所生成的随机序列的统计检验


三、服从其他概率分布的伪随机数
由于最初的数字水印本身就是一个服从随机分布的正态矩阵，我们不仅要求能够得到均匀分布的随机序列, 还要求得到任意分布的随机序列, 这才能适应信息隐藏学科的需要。
1.构造的一般思路：
① 产生均匀分布随机序列 X{x1, x2, …, xn } ;
② 令 yi = G^- 1( xi) ;
③ 则随机序列 Y{y1, y2, …, yn }即为所求。
2.对于序列 Y, 满足:

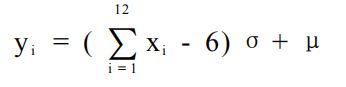
即得到服从 N( μ, σ^2) 的特性。

在 MATLAB 中, randn. m 函数就是依照式( 2. 26 ) 编写的产生正态分布随机数的
函数。
3.正态分布随机序列的统计检验
引入 正态概率纸检验法
MATLAB 中的正态概率纸函数是 normplot 函数。标准正态分布函数在正态坐标下是一条直线。
故经过操作

>> ans = randn( 1, 1000) ;
>> ans2 = randU1 ( 1, 1000, 100, 0, 1) ;
>> normplot( ans) ; hold on; normplot( ans2) ;

若所得为直线，随机序列即服从正态分布。

四、具有混沌特性的伪随机数
1.下面是 Logistic 方程产生混沌序列的 MATLAB 函数 randCL. m。
文件名: randCL. m
%目的: 利用 Logistic 方程产生混沌序列
应用举例: a = randCL( 10, 10, 0. 5, 3. 9 )
参数说明: 此函数产生一个序列矩阵
row: 为矩阵的行
col: 为矩阵的列
seed: 为初值( 0 到 1)
u : 即为公式中的 μ( 大于 3. 5699 小于等于 4)
%

function randmtx = randCL( row, col, seed, u)
randmtx( 1, 1) = seed;
for i = 2∶row* col
randmtx( 1, i) = u* randmtx( 1, i - 1) * ( 1 - randmtx( 1, i - 1) ) ;
end
randmtx = reshape( randmtx, row, col) ;

在一些数字水印算法中, 就是将生成好的混沌序列按照某种规则把它转化为需要的 0, 1 二值序列作为数字水印嵌入载体的。这时的水印与混沌序列有相同的性质, 就是与初值紧密相关。
2.混合光学双稳模型产生的混沌序列
迭代方程的形式为:
xn + 1 = Asin^2·( xn - xB )
这里有两个参数 A, xB , 分别取 4 和 2. 5, 此时方程处于混沌状态, 赋给它不同的初值 x0 将得到不同的混沌序列, 下面同样给出它的 MATLAB 函数 randCS. m。
%目的: 由混合光学双稳模型生成混沌序列
% 应用举例: a = randCS( 10, 10 , 0. 5) ;
% 参数说明: 此函数产生一个序列矩阵,
% row 为矩阵的行
% col 为矩阵的列
% seed 为初值( 0 到 1) 即公式中初值 X0
% 这里固定取 A = 4 , Xb = 2. 5

function randmtx = randCS( row, col, seed)
A = 4;
Xb = 2. 5;
randmtx( 1, 1) = seed;
for i = 2∶row* col
randmtx( 1, i) = A* sin( randmtx( 1, i - 1 ) - Xb) * sin ( randmtx( 1, i - 1 ) -
Xb) ;
end
randmtx = reshape( randmtx, row, col) ;

五、其他伪随机数发生器
1.N 级线性最长反馈序列( m 序列)
下面我们用 MATLAB 编写一个函数, 来产生这一序列。函数名叫做 mrand. m。
在函数中使用一个 connection 数组表示连接多项式。

function [ seq] = mrand( connection)
m = length( connection) ;
L = 2^m - 1;
registers = [ zeros( 1, m - 1 ) 1] ;
seq( 1) = registers( m) ;
for i = 2∶L
new_reg_cont( 1) = connection( 1) * seq( i - 1) ;
for j = 2∶m
new_reg_cont( j) = bitxor( registers( j - 1) , connection( j) * seq( i - 1 ) ) ;
end
registers = new_reg_cont;
seq( i) = registers( m) ;
end

2.伪随机组合发生器的一般原理
组合发生器是指用几个不同的随机数发生器组合所得到的一种发生器。
组合发生器一算法描述如下:
① 用混沌映射( RandCL) 产生 N 个随机数, 存放在矢量 L = ( l1
, l2
, …, l N ) 中。
② 用线性同余发生器( RandU1 ) 产生一个小于 N 的随机整数 k。
③ 令 rn = lk 。然后利用混沌映射( RandCL) 再产生一个随机数 temp, 令l k = temp。
④ 重复②③得到新的随机序列{ r n }。

六、随机序列在信息隐藏中的运用
1.随机序列与信息嵌入位的选择
Kerckhoffs 原则是信息安全的一个基本原则, 即系统的安全仅仅依赖于密钥而不是安全算法。因此，我们使用随机序列控制信息嵌入位。
常见的随机数控制的方法有两个: 随机间隔法和随机置换法。本节主要介绍随机间隔法。随机间隔法的思想比较简单, 主要是利用随机数的大小控制前后两个嵌入位的距离。

该程序是一个严格意义上的随机间隔选择隐藏位的程序
function [ row, col] = randinterval( matrix, count, key)
% 计算间隔的位数
[ m, n] = size( matrix) ;
interval1 = floor( m* n / count) + 1;
interval2 = interval1 - 2;
if interval2 == 0
error( ′载体太小不能将秘密信息隐藏进去! ′) ;
end
% 生成随机序列
rand( ′seed′, key) ;
a = rand( 1, count) ;
% 初始化
row = zeros( [ 1 count] ) ;
col = zeros( [ 1 count] ) ;
% 计算 row 和 col
r = 1;
c = 1 ;
row( 1, 1) = r;
col( 1, 1) = c;
for i = 2∶count
if a( i) > = 0. 5
c = c + interval1;
else
c = c + interval2;
end
if c > n
r = r + 1;
if r > m
error( ′载体太小不能将秘密信息隐藏进去! ′) ;
end
c = mod( c, n) ;
if c == 0
c = 1;
end
end
row( 1, i) = r;
col( 1, i) = c;
end

2.安全 Ha sh 函数
在随机置换法中, 由于对随机序列不加任何的限制, 不恰当的置换策略将很容易导致选择的像素位重复出现多次, 从而造成一个像素嵌入了多个信息, 后嵌入的信息破坏了先嵌入的信息, 我们称这种情况为碰撞( collision) 。解决碰撞的机制有很多,如数据结构中的开地址法等。这里我们将使用到安全 Hash 函数的伪随机置换算法,该算法可以解决碰撞问题。
Hash 函数的作用是将任意长度的报文映射为一个长度固定的 Hash 码。Hash码是报文每一位的函数。报文任意一位的改变都将导致 Hash 码的改变。常用的安全 Hash 函数有: MD5 , SHA-1 等。这里, 我们使用 MD5。
MD5 算法运算步骤如下:
( 1 ) 填充报文
( 2 ) 初始化缓冲区
( 3 ) 循环执行压缩函数
( 4 ) 输出 Hash码