【深度学习】【注意力机制】【自然语言处理】【图像识别】深度学习中的注意力机制详解、self-attention
1、深度学习的输入
无论是我们的语言处理、还是图像处理等,我们的输入都可以看作是一个向量。通过Model最终输出结果。这里,我们的vector大小是不会改变的。
然而,我们有可能会遇到这样的情况:
输入的sequence的长度是不定的怎么处理?
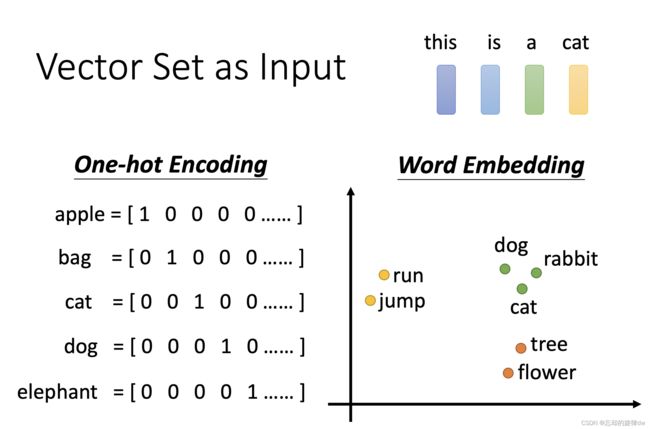
比如 Vector Set as Input:
- 句子:句子的词数不一定相同。
2、深度学习的输出
2.1 输出和输入数量相同
也就是说,输入的每一个向量,都对应一个输出标签。比如输入3个向量,输出3个对应标签。
例子:
- 输入一句话“I saw a saw”,输出4个标签,分析各个词的词性。
- 输入四个向量组成的一段音频,输出这四个向量代表的语意,比如这语音说的是“a、a、b、b”
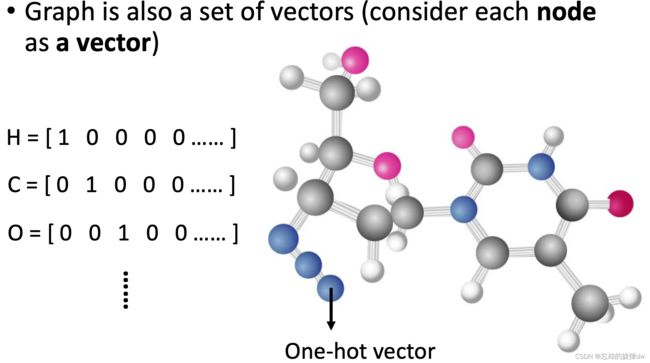
- 输入很多节点向量,构成一个图,输出各个节点所代表的重要含义。

2.2 输入多个向量,输出一个标签
这是说,我们输入了若干个向量,输出一个标签来描述这些向量的含义。
例子:
2.3 不知道要输出多少,机器自己决定
输入一些向量,输出的向量个数是不定的。
例子:
3、Sequence Labeling
这种情况对应上面的[[#2.1输出和输入数量相同]]。
看下面的例子:输入“I saw a saw”,我们的目标是输出每个词的对应词性。

然而这里有个问题:第一个saw和第二个saw词性不同,但通过model的输出却是相同的
因为每个词是独立的,所以要让它model考虑上下文信息。如何解决?
前后几个向量建立关系,添加FC:

FC可以让相邻的词语建立关系(相当于一个window),从而能帮助model推断。
然而这个办法有局限:如果我们考虑整个上下文的关系呢?把window开到最大?换言之:如果我们输入的句子有很多,长短不一,选取其中最长的句子的大小作为window,这样可行吗?答案是:这样会让FC的计算量非常大,还容易overfitting。
可以考虑self- attention。
4、Self- attention
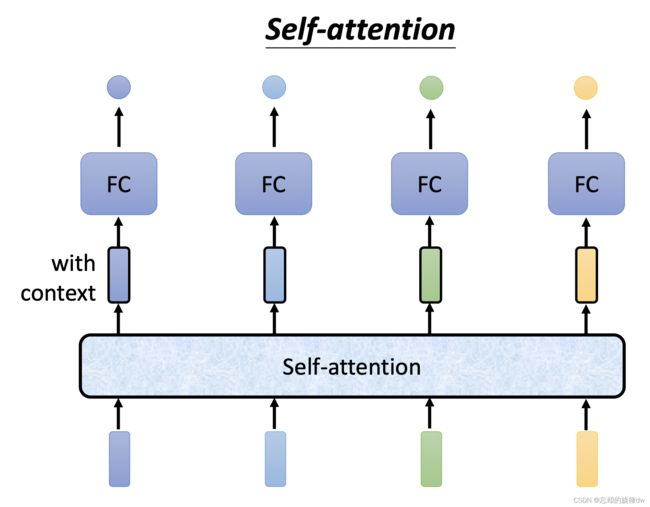
这里带有黑框的vector表示是携带了上下文的vector。
而且self-attention是可以叠加使用的。比如,可以先self- attention后,再进行FC,然后接着self-attemtion…
这就是著名的论文[[Attention_Is_All_You_Need.pdf]]。在这里,Google提出了transformer概念。其实在这之前有其它相近的概念,只是这片论文将这种概念发扬光大。
这里,输入的向量 [ a 1 , a 2 , a 3 , a 4 ] [a^1,a^2,a^3,a^4] [a1,a2,a3,a4] 建立好关系后 [ b 1 , b 2 , b 3 , b 4 ] [b^1,b^2,b^3,b^4] [b1,b2,b3,b4],完成context的获取。
下面以 b 1 b^1 b1的为例,讲述过程:
4.1 向量相关性
对于 a 1 a^1 a1,我们希望找出与它相关的向量,而不是整个sequence。

a 1 a^1 a1的和其他向量的相关程度的数值,用 α \alpha α 表示。
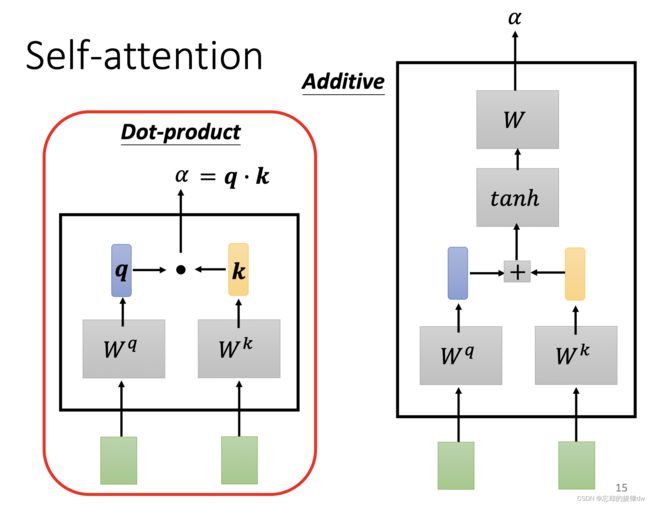
那么如何来找某两个向量之间的关系?比如以 a 1 a^1 a1和 a 4 a^4 a4?举两个例子:
- Dot-product
- Additive
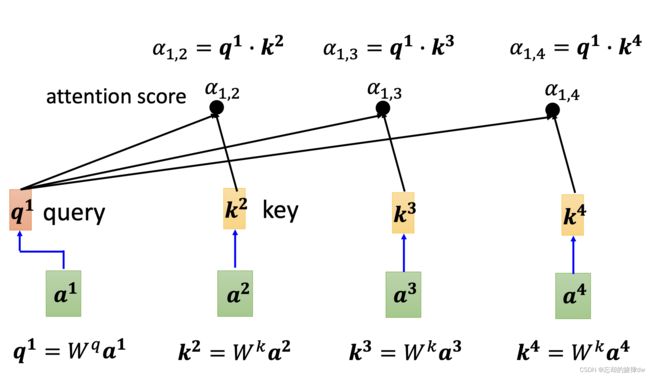
Dot- product:
这是一个常见的计算方法。首先,两个向量分别点乘以不同的向量 W q 和 W^q和 Wq和 W k W^k Wk,得到 q q q和 k k k,然后点乘得到结果 α \alpha α(attention score)。
其实,以 a 1 a^1 a1为例,自己也要和自己计算关联性:
接着,每个 α ′ \alpha' α′分别和 v ′ v' v′ 点乘求和。如果,举个例子, a 1 a^1 a1和 a 2 a^2 a2的关联性较强,那么 b 1 b^1 b1和 v 2 v^2 v2的值会更相近。

4.2 相关性计算细节
4.2.1 q q q、 k k k和 v v v的来源
对于一个向量 a a a,为了对应的 q q q、 k k k和 v v v,每个 a a a需要点乘以一个矩阵 W W W。因为这个W是固定的,所以可以把 a a a合并成一个大矩阵。以 q i q^i qi为例:首先 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4可以合成一个大矩阵 I I I,然后点乘以一个矩阵 W q W^q Wq,得到大矩阵 Q Q Q(可以拆成死列, q 1 q^1 q1、 q 2 q^2 q2、 q 3 q^3 q3、 q 4 q^4 q4)。 k k k和 v v v以此类推。如下图:
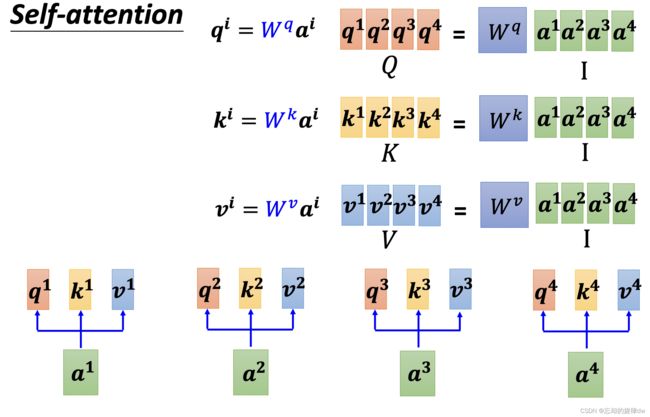
4.2.2 α \alpha α的计算
以 b 1 b^1 b1为例,在计算 b 1 b^1 b1前,我们需要先计算向量 a 1 a^1 a1与 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4的关系,即 α 1 , 1 \alpha^{1,1} α1,1、 α 1 , 2 \alpha^{1,2} α1,2、 α 1 , 3 \alpha^{1,3} α1,3、 α 1 , 4 \alpha^{1,4} α1,4。而对于计算公式中 a 1 , i = k i × q 1 a^{1,i}=k^i\times q^1 a1,i=ki×q1来说, q 1 q^1 q1是不变的。所以可以合并几个 k i k^i ki成一个大矩阵来计算,如下图:
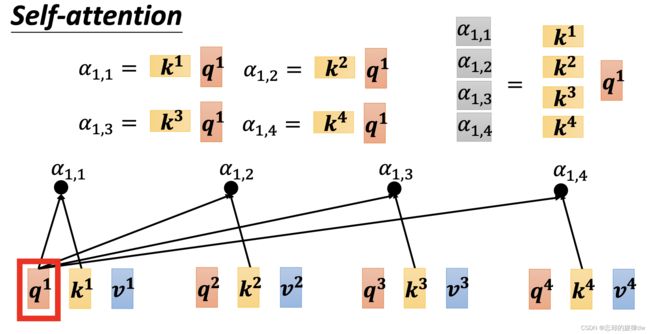
推广到 a i , i a^{i,i} ai,i,在经过normalization(用的是softmax,也可以选其他的如relu)就是:
4.2.3 b b b的计算
以 b 1 b^1 b1为例, b 1 b^1 b1的计算公式是: b 1 = α 1 , 1 ′ × v 1 + α 1 , 2 ′ × v 2 + α 1 , 3 ′ × v 3 + α 1 , 4 ′ × v 4 b^1=\alpha'_{1,1}\times v^1+\alpha'_{1,2}\times v^2+\alpha'_{1,3}\times v^3+\alpha'_{1,4}\times v^4 b1=α1,1′×v1+α1,2′×v2+α1,3′×v3+α1,4′×v4
写成矩阵形式就是:
b 1 = [ v 1 v 2 v 3 v 4 ] [ α 1 , 1 ′ α 1 , 2 ′ α 1 , 3 ′ α 1 , 4 ′ ] b^1= \begin{bmatrix} v^1&v^2&v^3&v^4 \end{bmatrix} \begin{bmatrix} \alpha'_{1,1}\\ \alpha'_{1,2}\\ \alpha'_{1,3}\\ \alpha'_{1,4} \end{bmatrix} b1=[v1v2v3v4] α1,1′α1,2′α1,3′α1,4′
以此类推,拓展到 b 2 b^2 b2、 b 3 b^3 b3、 b 4 b^4 b4就是:
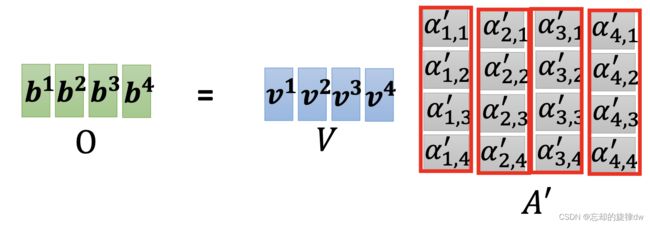
4.2.4 计算过程小结
重新再来看一遍这些计算过程,其实就是一些矩阵的运算。模型要学习的,其实就是 W q W^q Wq、 W k W^k Wk和 W v W^v Wv这三个矩阵。

5、multi-head attention
我们还可以用不同的 q q q来处理不同的相关性。下面举一个2个头的例子。我们的 a i a^i ai首先点乘以一个矩阵,得到了 q i q^i qi,然后 q i q^i qi再分别点乘以不同的两个矩阵,得到 q i , 1 q^{i,1} qi,1和 q i , 2 q^{i,2} qi,2。如下:
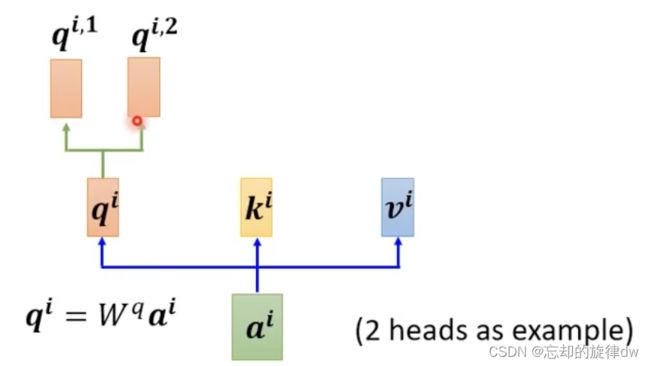
对应地,我们的 k k k和 v v v也需要分别有两个,也就是如下所示的样子:

接着,我们要继续计算 b b b。因为我们的 q q q、 k k k和 v v v各自都是2个,所以我们的 b b b也是分开算。首先通过 q i , 1 q^{i,1} qi,1、 k i , 1 k^{i,1} ki,1、 v i , 1 v^{i,1} vi,1计算得到 b i , 1 b^{i,1} bi,1。如下:

然后,相同地,通过 q i , 2 q^{i,2} qi,2、 k i , 2 k^{i,2} ki,2、 v i , 2 v^{i,2} vi,2计算得到 b i , 2 b^{i,2} bi,2。如下:
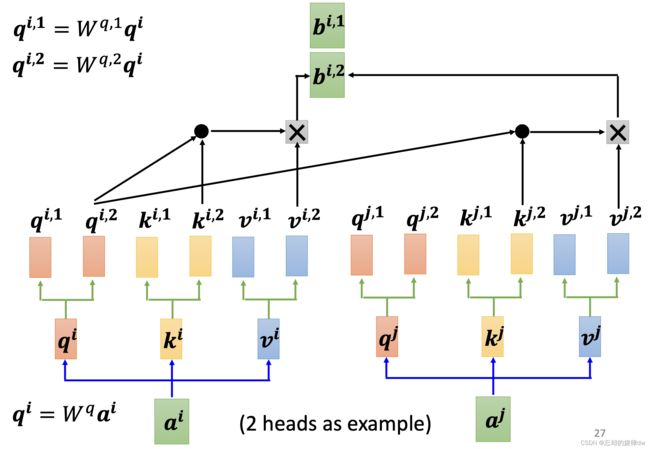
更多头的操作也是如此。
思考:对于一个向量,我们已经能够通过注意力机制,获取上下文信息了,但是好像没有考虑到空间信息。换言之,一些相同的向量通过模型的运算后,输出的结果是相似的,即使这些向量所处位置不同。比如,在我们的语句中,动词出现在句首的可能性很小。也就是说,如果一个词出现在句首,那么它大概率不是动词。
举个例子:“can”这个单词包含两个意思,“可以”和“罐头”。在这句话中:“罐头可以装食物。”,“A can can store food.”。句首的“can”是名词,而不是(情态)动词。这也是很重要的语义信息,然而,上面的注意力机制并没有注意到。
下面,将介绍包含位置信息的注意力机制。
6、Positional Encoding
为了让向量 a i a^i ai携带位置信息,可以让它加上位置向量 e i e^i ei。 e i e^i ei的i表示处在i的位置。比如 e 1 = [ 1 , 0 , 0 , 0 ] e^1=[1,0,0,0] e1=[1,0,0,0]表示处在1的位置, a 1 a^1 a1加上它后,就代表 a 1 a^1 a1处在1的位置; e 2 = [ 0 , 1 , 0 , 0 ] e^2=[0,1,0,0] e2=[0,1,0,0]表示处在2的位置, a 2 a^2 a2加上它后,就代表 a 2 a^2 a2处在2的位置(这里的向量是我举例随意写的)。
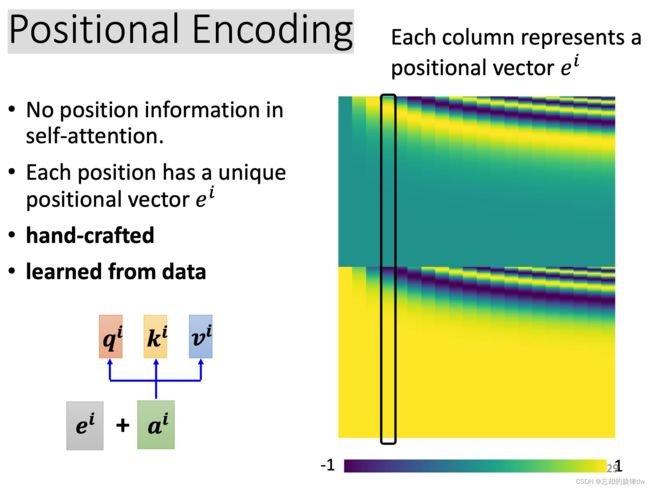
比如在上面图中的第四列,用黑框圈起来的这列代表 e 4 e^4 e4,他可以加到 a 4 a^4 a4上,代表这个 a 4 a^4 a4处在位置4上。
说明:这里的 e i e^i ei是hand-crafted的,也就是人工标注的。
这就有一个问题:如果向量 e e e设置的长度是128,但是我的语句sequence长度是129怎么办?这尚待研究。这有一篇论文研究了这个问题: 《Learning to Encode Position for Transformer with Continuous Dynamical Model》
7、Self- attention的应用
7.1
Transformer、BERT都是利用了自注意力机制。
7.1 Self-attention用在语音上
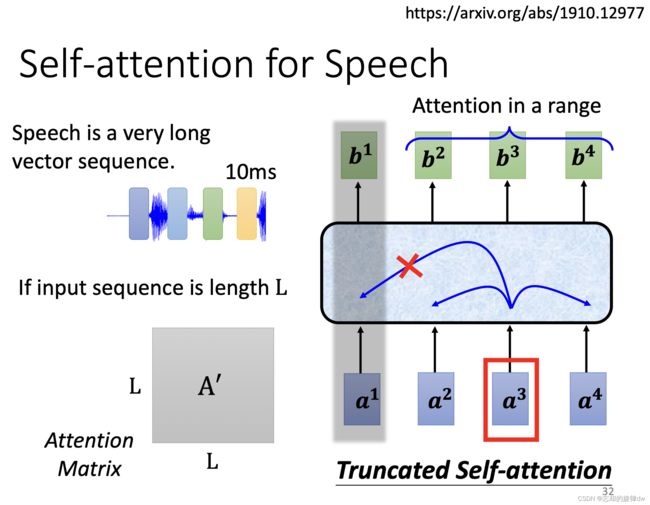
因为即使很短的语音信号转化的向量也是很长的,所以我们随俗便便说的一句语音可能就是上千长度的向量了。这就带来一个问题:矩阵 A ′ A' A′(就是那些很多 a 1 , 1 ′ a'_{1,1} a1,1′、 a 1 , 2 a_{1,2} a1,2、 a 1 , 3 a_{1,3} a1,3的矩阵)的行列会很大,导致占用训练内存很多,难以训练。解决办法是,输入的某个向量不要考虑全部上下文,而是只考虑相邻的几个向量,这样可以加快训练。
![[Pasted image 20240126013029.png]]
7.1 Self-attention用在图像上
对于一张图片来说,一个个像素可以用RGB三个通道表示。这些像素排列起来其实就是一个比较长的向量(把图片拉成一条直线)。这样,如果一个batch的输入是一排向量的话,适合用self-attention。
# 《Self-Attention Generative Adversarial Networks》
举例2:
# 《End-to-End Object Detection with Transformers》
8、Self-attention v.s CNN
我们在使用Self-attention处理图像时,一个pixel(像素)产生query,其他pixel产生key。
以上面我们说的为例,我们使用的是内积(点乘)运算,所以self-attention考虑的是全局资讯(上下文信息)。
而在CNN中,一个neuron只考虑感受野(receptive field)内的讯息。
所以,可以说,CNN是简化版的self- attention;self- attention是CNN的复杂版。
也可以说,self-attention在找出相关的pixel时,像是在自动学习感受野的形状、哪些pixel时重要的、相关的。

下面这篇论文阐述了CNN和self-attention的关系:设置好self-attention的参数,可以做到和CNN一模一样的效果。
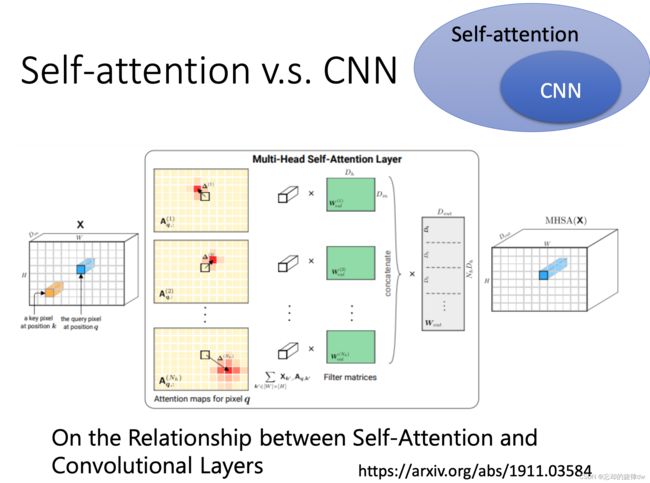
# 《On the Relationship between Self-Attention and Convolutional Layers》
未完待续…读完资料再来更新