代码随想录---数组笔记
一、数据结构的定义
数据结构: 数据结构是计算机存储、组织数据的方式。
数据结构大致可划分为三类:线性结构、树形结构、图形结构。

其中他们各自,又细化出了更多子结构,比如:
线性结构*(线性表)
- 数组
- 链表
- 栈
- 队列
- 哈希表(散列表)
ps: 哈希表是一种特殊的线性表,采用了哈希算法。同时有链表和线性表的优点,但占的空间大,牺牲空间换取了效率。
树形结构
- 二叉树(完全二叉树、满二叉树、平衡二叉树)
- 堆
- Trie(字典树)
- B树
- 红黑树
- 哈夫曼树
- 并查集
图形
- 结构
- 邻接矩阵
- 临接表
二、数组的定义
数组是存放在连续内存空间上的相同类型数据的集合
线性表是具有n个相同类型元素的序列。
注意:
(1)下标索引:数组下标都是从0开始的
(2)内存空间地址连续:删除或者增加元素时,要移动其他元素3的地址
(3)数组的元素是不能删的,只能覆盖
三、数组的操作
1、数组的初始化
在Python中,list由于为动态数组,所以初始化可以很随意:
li = []
li = list()
li = [1, 2, 3, 4, 5]2、数组的遍历
Python在数据的遍历,都可以分为两种:
(1)下标访问
li = [1, 2, 3, 4, 5]
for i in range(len(li)):
print(li[i])(2)直接遍历每个元素
for i in li:
print(i)
# 特殊的 enumerate操作,方便同时获取下标与内容
for index, val in enumerate(li, start=0):
print(f"index:{index},value:{val}")3、#打印数组内存地址
print(id(li)) # 20207790578004、数组排序
# li.sort()原地修改
li = [1, 3, 2, 4, 5]
print(li) # [1, 3, 2, 4, 5]
li.sort()
print(li) # [1, 2, 3, 4, 5]
# sorted(li)创建新数组并返回
li = [1, 3, 2, 4, 5]
new_li = sorted(li)
print(new_li) # [1, 2, 3, 4, 5]
5、循环不变量规则
循环---->边界处理----->区间的定义---->不变量
四、经典数组题目
四道经典数组题目,每一道题目都代表一个类型,一种思想。
1、二分查找
(1)例题 704. 二分查找
(2)思路
1.前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的。
2.循环不变量规则:一般采用左闭右闭区间,也就是[left, right] 。
3.注意循环条件:while left <= right:
4.注意return -1不要放进else中,以免查找的target不存在时,返回的是None,而不是-1
(3)复杂度分析:
时间复杂度: O(logn)
空间复杂度:O(1)
(4)代码
def search(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1
while left <= right: # 候选区有值
mid = (left + right) // 2
if nums[mid] > target:
right = mid -1
elif nums[mid] < target:
left = mid + 1
else:
return mid
return -1 # 根据题意变化(5) 相关题目推荐(力扣)
- 35.搜索插入位置
35.搜索插入位置–讲解
- 34.在排序数组中查找元素的第一个和最后一个位置【中等】
- 69.x 的平方根
- 367.有效的完全平方数
(6) 总结
注意while循环结束后的return语句
2、双指针法
(1)例题 27. 移除元素
(2)思路
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。【常量级空间复杂度】
1.普通双指针
(3)复杂度分析:
时间复杂度:O(n),其中 n 为序列的长度。只需要遍历该序列至多两次。
空间复杂度:O(1)
(4)代码
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
n = len(nums)
left = 0 # left是慢指针,指向下一个将要输出的位置
for right in range(n): # right是快指针,指向当前将要处理的元素(遍历)
if nums[right] != val: # 则nums[right]肯定要输出,要放到left位置上
nums[left] = nums[right]
left += 1 # 左右指针同时右移(右指针是循环自动右移)
# 当nums[right] == val:只有右指针因为循环自动右移
return left # left 的值就是最终要输出数组的长度2.双指针优化
复杂度分析:
时间复杂度:O(n),其中 n 为序列的长度。只需要遍历该序列至多一次。
空间复杂度:O(1)
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
n = len(nums)
left = 0 # 两个指针初始时分别位于数组的首尾,向中间移动遍历该序列
right = n - 1
while left < right: # 左右指针重合时,遍历完数组中所有的元素
if nums[left] == val:
nums[left] = nums[right-1]# 将right指向的元素复制到left 的位置,即删除了left位置上的原值
right -= 1 # right 左移一位
left += 1 # left 右移一位
return left
~~nums[left] = nums[right]~~为什么不是这句???
(5) 相关题目推荐(力扣)
- 26.删除排序数组中的重复项
- 283.移动零
- 844.比较含退格的字符串
- 977.有序数组的平方
(6) 总结
left是慢指针,指向下一个将要输出的位置;
right是快指针,指向当前将要处理的元素
left 的值就是最终要输出数组的长度
使用 O(1) 额外空间并 原地 修改输入数组。
- 普通双指针法:
元素的相对位置没有发生改变
left和right指针都是从0开始
for循环遍历right(也可改成while循环)
只需要遍历该序列至多两次
- 双指针法优化:
元素的相对位置发生了改变
left指针从0开始,right指针从n-1开始;向中间移动遍历该序列。
while循环left < right
只需要遍历该序列至多一次
避免了需要保留的元素的重复赋值操作
3.双指针法的扩展
双指针法将时间复杂度O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级,题目如下:
- 15.三数之和
- 18.四数之和
双指针来记录前后指针实现链表反转:
- 206.反转链表
使用双指针来确定有环:
- 142题.环形链表II
3、通用解法
(1)例题 26.删除排序数组中的重复项
(2)思路
「通用解法」是一种针对「数据有序,相同元素最多保留 k 位」
- 由于是保留 k 个相同数字,对于前 k 个数字,我们可以直接保留。
- 对于后面的任意数字,能够保留的前提是:与当前写入的位置前面的第 k 个元素进行比较,不相同则保留。
复杂度分析
时间复杂度:O(n)
空间复杂度:O(1)
代码
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
def process(nums, k): # 保留 k 个相同数字
idx = 0 # idx,指向待插入位置
# idx < k: 直接保留前 k 个数字
# nums[idx-k] != x: 保留与前 k 个数字不相同的
for x in nums:
if idx < k or nums[idx-k] != x:
nums[idx] = x
idx += 1
return idx
return process(nums, 1) #调用函数 (3) 相关题目推荐(力扣)
- 80. 删除有序数组中的重复项 II
4、滑动窗口
(1)例题
209.长度最小的子数组
(2)思路:
滑动窗口:不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。
详细过程:
定义两个指针 start 和end 分别表示子数组(滑动窗口窗口)的开始位置和结束位置,维护变量 sum 存储子数组中的元素和(即从 nums[start] 到 nums[end] 的元素和)。
初始状态下,start 和end 都指向下标 0,sum 的值为 0。
每一轮迭代,将 nums[end] 加到 sum,如果 sum≥s,则更新子数组的最小长度(此时子数组的长度是 end−start+1),然后将 nums[start] 从 sum 中减去并将 start 右移,直到 sum (3)复杂度分析 时间复杂度:O(n),其中 n 是数组的长度。指针 start 和 end 最多各移动 n 次。 (4)代码 (5) 相关题目推荐(力扣) (6)总结 (1)例题 59. 螺旋矩阵 II (2)思路 本题并不涉及到什么算法,就是模拟过程。 方法:按层模拟 可以将矩阵看成若干层,首先填入矩阵最外层的元素,其次填入矩阵次外层的元素,直到填入矩阵最内层的元素。 定义矩阵的第 k 层是到最近边界距离为 k 的所有顶点。例如,下图矩阵最外层元素都是第 1 层,次外层元素都是第 2 层,最内层元素都是第 3 层。 [[1, 1, 1, 1, 1, 1], (3)复杂度分析 时间复杂度:O(n2 ),其中 n 是给定的正整数。矩阵的大小是 n×n,需要填入矩阵中的每个元素。 (4)代码 (5) 相关题目推荐(力扣) 54. 螺旋矩阵【中等】 剑指Offer 29.顺时针打印矩阵 (6)总结 逆序输出【大数在前,小数在后,左闭右开】 设定好边界值坚持循环不变量原则【左闭右开】
空间复杂度:O(1)。class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
if not nums: # 数组为空
return 0
n = len(nums)
start = end = 0 # 滑动窗口的起始位置指针start;结束位置指针end
sum = 0 # sum存储连续子数组的和,初始值为0
res = n + 1 # res存储子数组的最小长度,初始值为较大的不可能值
# 或者 res = float("inf") # 定义一个无限大的数
while end < n:
sum += nums[end]
while sum >= target: # sum可能要循环减去nums[start],所以用while,而不是if
res = min(res, end - start + 1) # 更新子数组的最小长度
## 准备缩小滑动窗口
sum -= nums[start] # sum里减去nums[start],直至sum
题目没看懂??跳过??
res = float("inf")
# 或者 超过数组长度
res = n + 1
end - start + 1
res = min(res, end - start + 1) # 自带min 函数,复杂度未知
## 两者相比较,可采用以下这种三元写法
res = res if res < end - start + 1 else end -start + 1
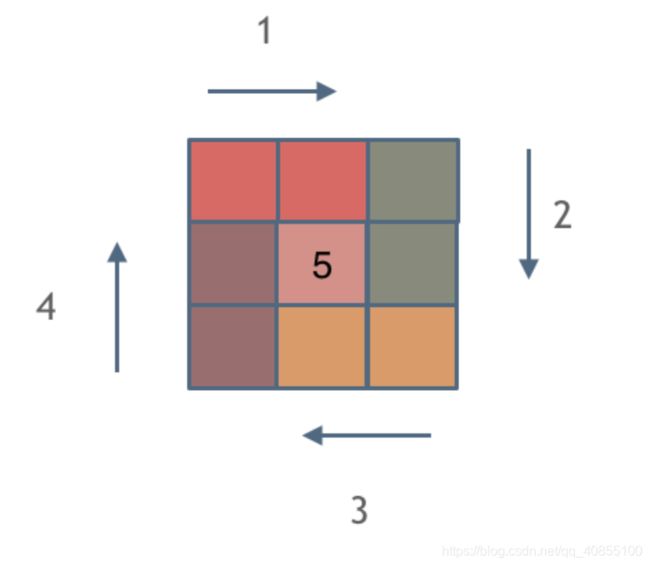
5、模拟法
[1, 2, 2, 2, 2, 1],
[1, 2, 3, 3, 2, 1],
[1, 2, 3, 3, 2, 1],
[1, 2, 2, 2, 2, 1],
[1, 1, 1, 1, 1, 1]]
对于每层,从左上方开始以顺时针的顺序填入所有元素。假设当前层的左上角位于 (top,left),右下角位于 (bottom,right),按照如下顺序填入当前层的元素。
![]()
空间复杂度:O(1)。除了返回的矩阵以外,空间复杂度是常数。class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
matrix = [[0]*n for _ in range(n)] # 初始化一个全0的n x n 正方形矩阵 matrix
left, right, top, bottom = 0, n-1, 0, n-1
num = 1 # num为填充元素,初始值为1
while left <= right and top <= bottom: # 边界条件
# 从左到右遍历top行的[left,righ]列
for col in range(left, right+1):
matrix[top][col] = num
num += 1
# 从上到下遍历right列的[top+1,bottom]行,注意range是左闭右开区间
for row in range(top+1, bottom+1):
matrix[row][right] = num
num += 1
# 从右到左遍历下侧元素,依次为(bottom,right−1) 到 (bottom,left+1)
for col in range(right-1,left, -1):
matrix[bottom][col] = num
num += 1
#从下到上遍历左侧元素,依次为 (bottom,left) 到 (top+1,left)
for row in range(bottom, top, -1):
matrix[row][left] = num
num += 1
#将 left 和 top 分别增加 1,将 right 和 bottom 分别减少 1,进入下一层继续遍历,直到遍历完所有元素为止。
left += 1
top += 1
right -= 1
bottom -= 1
return matrix
for i in range(5,2,-1):
print(i)
# 输出
5
4
3不懂54. 螺旋矩阵为什么必须加上if判断语句,不加会出错?
而59. 螺旋矩阵II加不加if判断语句,都不会出错??不懂我按照左闭右开为什么和他们表示的不同??