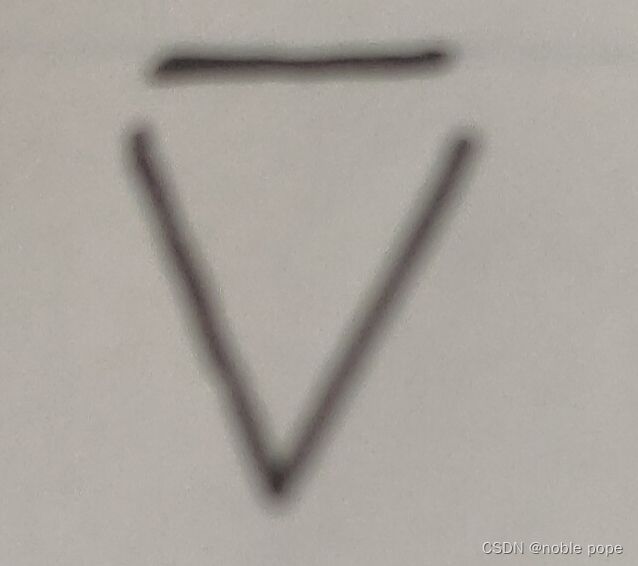离散数学——命题逻辑、谓词逻辑、集合与关系知识点
一、命题逻辑
一、命题及其表示法
命题的定义:具有确定真值的陈述句。
二、联结词(简单不做赘述)
1.否定:¬
2.合取:∧
3.析取:∨
4.条件:→
5.双条件:↔
三、命题公式与翻译
四、真值表与等价公式
1.真值表:根据命题公式的真值可简单构建,示例:构造¬P∨Q的真值表如下
| P | Q | ¬ P | ¬P∨Q |
| T | T | F | T |
| T | F | F | F |
| F | T | T | T |
| F | F | T | T |
2.等价公式:
对合律:¬¬P⇔P;
幂等律:P∨P⇔P,P∧P⇔P;
结合律:(P∨Q)∨R⇔P∨(Q∨R),(P∧Q)∧R⇔P∧(Q∧R);
交换律:P∨Q⇔Q∨P,Q∧P⇔P∧Q;
分配律:P∨(Q∧R)⇔(P∨Q)∧(P∨R),P∧(Q∨R)⇔(P∨Q)∧(P∨R);
吸收律:P∨(P∧Q)⇔P,P∧(P∨Q)⇔P;
德摩根律:¬(P∨Q)⇔¬P∧¬Q,¬(P∧Q)⇔¬P∨¬Q;
同一律:P∨F⇔P,P∧T⇔P;
零律:P∧F⇔F,P∨T⇔T;
否定律:P∨¬P⇔T,P∧¬P⇔F;
五、重言式与蕴含式
1.重言式(永真公式):无论对分量作怎样指派,真值永远为T的命题。
2.矛盾式(永假公式):无论对分量作怎样指派,真值永远为F的命题。
3.蕴含式:当且仅当P→Q是一个重言式时,我们称“P蕴含Q”,记作P⇒Q
P⇔Q的充要条件:P⇒Q,P⇒Q;
4.对P→Q:它的逆换式:Q→P;反换式:¬P→¬Q;逆反式:¬Q→¬P,
P→Q⇔¬Q→¬P。
六、其他联结词
1.不可兼析取:⊕,手写写为
P⊕Q,只有当P和Q一真一假时,它的真值为真,否则为假
2.条件否定:P条件否定Q,只有P为真Q为假时才为真。
3.与非和或非:与非↑,或非↓。性质:
P↑Q⇔¬(P∧Q)
P↑P=¬(P∧P)=¬P
P↓Q⇔¬(P∨Q)
P↓P=¬(P∨P)=¬P
七、对偶与范式
1.对偶式:在命题A中将所有∧和∨互换,F和T互相取代,即得到对偶式A*。
性质:¬A(P1,P2,...,Pn)⇔A*(¬P1,¬P2,...,¬Pn)
A(¬P1,¬P2,...,¬Pn)⇔¬A*(P1,P2,...,Pn)
2.范式
合取范式:A1∧A2∧A3∧...∧An;析取范式A1∨A2∨A3∨...∨An
求范式的步骤:(1)将公式中联结词全换成∨∧¬,(2)将¬移到各命题元之前(3).分配结合律调整。
主析取范式:全是小项,小项内全是∧,小项的编码:真为1,假为0,
例如:主析取范式(¬P∧Q)∨(P∧Q)编码表示为m01∨m11,表示为![]() 1,3
1,3
主合取范式:由大项组成,大项内全是∨,大项编码:真为0,假为1,
例如:主合取范式(¬P∨Q)∧(P∨Q)编码表示为M10∧M00,可表示为![]() 0,2
0,2
求得主和/析取范式即可得到主析/合取范式,根据编码,如大小项中有3个元素,则有2*2*2=8个编码:假设得到的是![]() 0,2,由此可直接推出主析取范式
0,2,由此可直接推出主析取范式![]() 1,3,4,5,6,7。
1,3,4,5,6,7。
八、推理理论
主要有大题证明,
1.规则说明:
P规则:每次引入前提时使用,
T规则:每次推出一个什么结论时使用
I:写在T之后,用于每次由已知推出某个东西时,体现为⇒
E:写在T之后,用于由前面的条件得到等价的东西时,体现为⇔
2.证明方法:
1.真值表法(不推荐,除非题目规定或木法)
2.直接证法:正向由前提一步步推出结论。
3.间接证法:(1)将要得的结论前加一个¬来当做条件,证明其与前提矛盾,反证引入这个一步需要“P(附加前提)”
(2)CP规则,常用与证明类似:***¥¥¥###⇒(R→C),的问题,此时将R作为前提条件:R P(附加前提),最后得出结论时格式应是R→C CP
二、谓词逻辑
一、谓词的概念与表示(应该没啥考点)
例如在命题:他是三好学生。
这个命题中“是三好学生”就是谓词
二、命题函数与量词
命题函数:通过举例学习:
如定义一个命题函数M(x):M(x):x是人。
量词:存在、所有等表示范围的词
三、谓词公式与翻译
举例说明:
翻译:这个蓝色的地板上放了一些零食。
设A(x):x是蓝色的;B(x):x是地板;C(x):x是零食;D(x,y):y放在x上
x:这个,y:一些
A(x)∧B(x)∧C(y)∧D(x,y)
四、变元的约束
约束变元:在一个公式中在ョ或∀定义范围内的变元,其他为自由变元。
换名:针对约束变元
代入:针对自由变元,规则是全覆盖并且不能和已有的重复。
五、谓词演算的等价式与蕴含式
本节主要有以下几个公式:
¬(∀x)P(x)⇔(ョx)¬P(x)
¬(ョx)P(x)⇔(∀x)¬P(x)
出现类似(∀x)(P(x)→Q)时可化简:(∀x)(¬P(x)∨Q)⇔¬(ョx)P(x)∨Q
六、前束范式
前束范式:一个公式,它的两次均在全式的开头,他们的作用域延伸至整个公式的末尾。
七、推理
规则介绍:
US:用于(∀x)P(x)变为P(a)
ES:用于(ョx)P(x)变为P(a)
UG:P(a)向(∀x)P(x)
EG:P(a)向(ョx)P(x)
三、集合与关系
一、集合的概念和表示法
全集:在一定范围内所有集合均为某一集合的子集,则该集合为全集,记为E。
幂集:给定集合A,由A的所有子集组成的集合。例如:A={a,b},则A的幂集为{∅,{a},{b},{a,b}}
二、集合的运算
集合的交:∩
集合的并:∪
满足分配律:A∩ (B∪C)=(A∩ B)∪ (A∩ C),互换也成立。
吸收率成立
集合的补:B对于A的补集,表示为A-B,集合元素全部属于A,不属于B。
~A:集合A的绝对补,即全集E-A。
公式:对集合A和B:
~(A∪B)=~A∩~B , ~(A∩B)=~A∪~B
A-B=A∩~B=A-(A∩B)
集合的对称差:通俗来讲就是两个集合相加后去掉两个集合的重叠部分。
A⊕B=(A-B)⊕(B-A)
三、包含排斥性原理
定理1:设A1,A2为有限集合,元素个数分别为|A1|,|A2|,则:|A1∪A2|=|A1|+|A2|-|A1∩A2|
推广到有3个、四个....n个集合的情况。
四、序偶和笛卡尔积
笛卡尔积:有集合A、B,在序偶中,第一个是A的元素,第二个是B的元素,这样的序偶集合称为笛卡尔乘积(直积):A×B={
五、关系及其表示
任意序偶确定了一个二元关系R,
在一个关系
Ix:X上的恒等关系,Ix={
六、关系的性质
自反,对任意x都有
对称,对任意
传递,对存在的任意xRy,yRz,都有xRz。
关系矩阵画法。
七、复合关系和逆关系
复合关系:R为X到Y的关系,S为Y到Z的关系,则R○S为R和S的复合关系。
复合关系的矩阵运算。
逆关系:将关系R中每个序偶的前后顺序互换,得到的Rᶜ是R的逆关系。
性质:
(R1∪R2)ᶜ=R1ᶜ∪R2ᶜ
(R1∩R2)ᶜ=R1ᶜ∩R2ᶜ
(A×B)ᶜ=B×A
(R1-R2)ᶜ=R1ᶜ-R2ᶜ
复合与逆关系性质:(T○S)ᶜ=Sᶜ○Tᶜ
若R对称:R=Rᶜ
若R反对称:R∩Rᶜ=Ix
八、关系闭包运算
自反闭包r(R)=R∪Ix
对称闭包s(R)=R∪Rᶜ
传递闭包t(R),先写出自身关系矩阵M1,用M1×M1得M2,M2×M1得M3,几阶矩阵就乘到M几,
最后把所有M1到Mn相加就是t(R)的关系矩阵。
九、集合的划分和覆盖
把集合A分成若干子集,使A中每个元素都至少属于其中一个子集,这些子集的集合叫A的覆盖。
如果每个元素属于且仅属于其中一个子集,那么这些子集的集合就叫做A的划分。
加细:若A有两个划分X,Y,对与Y中每个Yi都有X中对应的Xi使得Yi⊆Xi,则称Y是X的加细。
十、等价关系和等价类
对于关系R,如果是自反、对称、传递的,那么R称为等价关系。
等价类:是一个元素的集合,例如:R是集合A上的等价关系,由元素a形成的等价类就是在集合R中所有与a有关的序偶形成的集合就是a形成的等价类。
A中等价类的集合则称为等价类的商集。记作A/R。
十一、相容关系
对于关系R,如果是自反的、对称的,则称R为相容关系。
相容类:存在相容关系的集合A中,能形成相容关系的元素子集,
最大相容类:加入任何元素都不再是相容类的相容类。
十二、序关系
满足自反、反对称性和传递性。
哈斯图画法。
全序关系
良序集合
全序集合