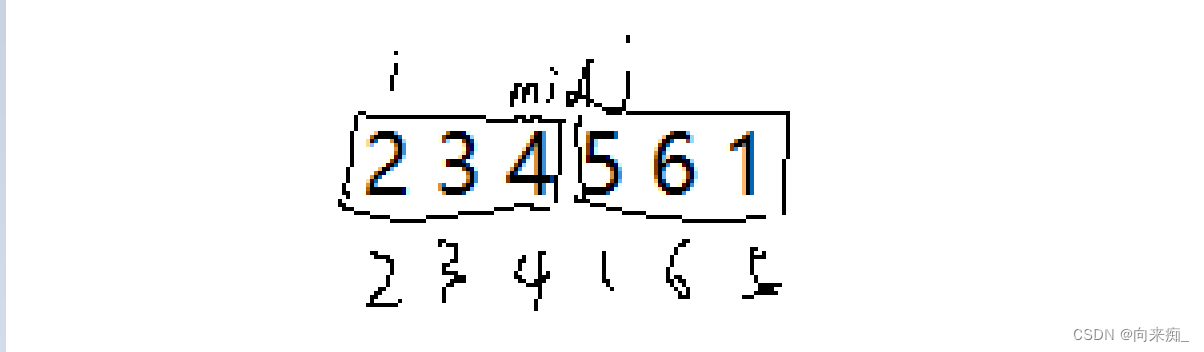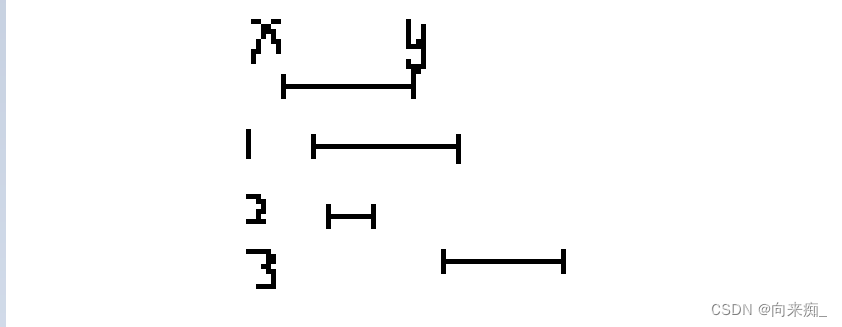算法基础课-基础算法
快速排序
题目链接:785. 快速排序 - AcWing题库
算法思想:找到一个数,让比其大的数放在这个数的左边,比这个小的数放在这个数的右边,并且递归处理所有子区间,这样就能保证整个序列有序。
#include
using namespace std;
void fzw_sort(int q[],int l,int r){
if(l == r) return;
int i = l-1,j=r+1,x=q[(l+r)/2];
// cout<x);
if(i>a[i];
fzw_sort(a,0,n-1);
for(int i=0;i 归并排序
题目链接:787. 归并排序 - AcWing题库
思路:将待排序的序列分成两个子序列,分别对这两个子序列进行递归排序,然后将排好序的子序列合并成一个有序的序列。
#include
using namespace std;
const int N = 100010;
int a[N];
int tmp[N];
void merge_sort(int a[],int l,int r){
if(l>=r) return ;
int mid = l+r>>1;
merge_sort(a,l,mid);merge_sort(a,mid+1,r);
int i = l,j = mid+1,k=0;
while(i<=mid&&j<=r){
if(a[i]<=a[j]) tmp[k++] = a[i++];
else tmp[k++] = a[j++];
}
while (i <= mid) tmp[k ++ ] = a[i ++ ];
while (j <= r) tmp[k ++ ] = a[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) a[i] = tmp[j];
}
int main(){
int n;
cin>>n;
for(int i=0;i>a[i];
merge_sort(a,0,n-1);
for(int i=0;i 题目链接:788. 逆序对的数量 - AcWing题库
题意:要求输出i
思路:对于每次归并排序,都会将区间分为左半和右半,左半的坐标一定小于右半,找出左半比右半数字大的数对即可。
首先思考应该在哪里对cnt计数结果增加,应该是遇到左半的a[i]>a[j]时,再思考应该增加多少,对于左半区间来说已经递增有序,所以左半区间目前枚举的数是最小的,所以需要增加mid-i+1个数,因为左半区间比a[i]大的数有mid-i个。
#include
using namespace std;
const int N = 100010;
int a[N];
int tmp[N];
int cnt = 0;
void merge_sort(int a[],int l,int r){
if(l>=r) return ;
int mid = l+r>>1;
merge_sort(a,l,mid);merge_sort(a,mid+1,r);
int i = l,j = mid+1,k=0;
while(i<=mid&&j<=r){
if(a[i]<=a[j]) tmp[k++] = a[i++];
else{
tmp[k++] = a[j++];
cnt+=mid-i+1;
}
}
while (i <= mid) tmp[k ++ ] = a[i ++ ];
while (j <= r) tmp[k ++ ] = a[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) a[i] = tmp[j];
}
int main(){
int n;
cin>>n;
for(int i=0;i>a[i];
merge_sort(a,0,n-1);
cout< 二分
选右区间的左端点时选第一个模板,选左区间的右端点时选第二个模板。
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}高精度
题目链接:791. 高精度加法 - AcWing题库
思路:倒着存储数字,方便进位,然后模拟加法过程即可。
// C = A + B, A >= 0, B >= 0
#include
using namespace std;
vector add(vector &A,vector &B){
if(A.size() C;
int t = 0;
for(int i=0;i>a;
cin>>b;
vector A;
vector B;
for (int i = a.size() - 1; i >= 0; i -- ){
A.push_back(a[i] - '0');
cout<= 0; i -- ) B.push_back(b[i] - '0');
// cout< C = add(A,B);
for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
return 0;
} 题目链接:792. 高精度减法 - AcWing题库
思路:需要先判断数字大小,然后模拟减法过程即可(模拟借位和去除前导零)。
// C = A - B, 满足A >= B, A >= 0, B >= 0
#include
using namespace std;
bool cmp(vector &A,vector &B){
if(A.size()!=B.size())
return A.size()>B.size();
for(int i=A.size()-1;i>=0;i--){
if(A[i]!=B[i]) return A[i]>B[i];
}
return true;
}
vector sub(vector &A,vector &B){
vector C;
int t = 0;
for(int i=0;i 1 && C.back() == 0) C.pop_back();
return C;
}
int main(){
string a,b;
cin>>a;
cin>>b;
vector A;
vector B;
for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
// cout< C;
if(cmp(A,B)) C = sub(A,B);
else{
cout<<"-";
C = sub(B,A);
};
for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
return 0;
} 题目链接:793. 高精度乘法 - AcWing题库
思路:模拟乘法(需要注意的是t+=a[i]*b以及去除前导零)。
// C = A * b, A >= 0, b >= 0
#include
using namespace std;
vector mul(vector &A,int b){
vector C;
int t = 0;
for(int i=0;i1&&C.back() == 0) C.pop_back();
return C;
}
int main(){
string a;
int b;
cin>>a;
cin>>b;
vector A;
// vector B;
for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
// for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
// cout< C = mul(A,b);
for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
return 0;
} 题目链接: 794. 高精度除法 - AcWing题库
思路:模拟除法(需要注意结果数组需要逆转以及去除前导零)
// A / b = C ... r, A >= 0, b > 0
#include
using namespace std;
vector div(vector &A,int b,int &r){
vector C;
r = 0;
for(int i=A.size();i>=0;i--){
r = r*10 + A[i];
C.push_back(r/b);
r%=b;
}
reverse(C.begin(),C.end());
while(C.size()>1&&C.back() == 0) C.pop_back();
return C;
}
int main(){
string a;
int b;
int r=0;
cin>>a;
cin>>b;
vector A;
// vector B;
for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
// for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
// cout< C = div(A,b,r);
for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
cout< 前缀和与差分
题目链接:795. 前缀和 - AcWing题库
思路:
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]
#include
using namespace std;
const int N = 100010;
int a[N];
int s[N];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) {
cin>>a[i];
s[i] = s[i-1] + a[i];
}
while(m--){
int l,r;
cin>>l>>r;
cout< 题目链接:796. 子矩阵的和 - AcWing题库
思路:画画格子就明白了。
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
#include
using namespace std;
const int N = 1010;
int a[N][N];
int s[N][N];
int main(){
int n,m,q;
cin>>n>>m>>q;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=m;j++){
cin>>a[i][j];
s[i][j] = s[i-1][j] + s[i][j-1] + a[i][j] - s[i-1][j-1];
}
while(q--){
int x1,x2,y1,y2;
cin>>x1>>y1>>x2>>y2;
cout< 题目链接:797. 差分 - AcWing题库
思路:差分是前缀和的逆运算,b[i] = a[i] - a[i-1],需要注意的是差分数组要和原数组区分开,不能在原数组的基础上直接进行差分的初始化,不然会出错,因为在差分初始化的过程中会改变原数组的数值。
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
差分的作用在于统一改变一段区间中的数字,统一加或减去某个数。
#include
using namespace std;
const int N = 100010;
int a[N];
int b[N];
void insert(int l,int r,int c){
b[l] += c;
b[r+1] -= c;
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
insert(i,i,a[i]); //构造a[i]的差分数组
}
while(m--){
int l,r,c;
cin>>l>>r>>c;
insert(l,r,c);
}
for(int i=1;i<=n;i++){
b[i] = b[i-1] + b[i]; //使用前缀和求原数组
cout< 题目链接:798. 差分矩阵 - AcWing题库
思路:给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
#include
using namespace std;
const int N = 1010;
int a[N][N];
int S[N][N];
void insert(int x1,int y1,int x2,int y2,int c){
S[x1][y1] += c;
S[x2 + 1][y1] -= c;
S[x1][y2 + 1] -= c;
S[x2 + 1][y2 + 1] += c;
}
int main(){
int n,m,q;
cin>>n>>m>>q;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=m;j++){
cin>>a[i][j];
insert(i,j,i,j,a[i][j]);
}
while(q--){
int x1,x2,y1,y2,c;
cin>>x1>>y1>>x2>>y2>>c;
insert(x1,y1,x2,y2,c);
}
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + S[i][j];
cout< 位运算
求n的第k位数字: n >> k & 1
返回n的最后一位1:lowbit(n) = n & -n
离散化
参考这个博客AcWing 802. 画个图辅助理解~ - AcWing,写的太好了。
区间合并
题目链接:803. 区间合并 - AcWing题库
思路:先对所有区间按左端点排序,对于当前已有区间,后面的区间分为以下三种情况,1情况更新y值,2情况不改变(可以结合1情况取最大值即可),3情况现将当前区间加入到结果集合中再更新x,y。
需要注意的是最后需要将x,y添加进结果数组,因为假如当前区间是倒数第二个区间,遇到以下三种情况时,1和2情况会更新y值,但不会将当前区间加入结果数组,3情况会更新x,y值,会将当前区间加入结果数组,但是最后一个区间不会加入到结果数组,所以需要在循环外添加进结果数组。
#include
#define x first
#define y second
using namespace std;
typedef pair PII;
int main(){
int n;
cin>>n;
vector a;
while(n--){
int l,r;
cin>>l>>r;
a.push_back({l,r});
}
sort(a.begin(),a.end());
// for(int i=0;i res;
int x = a[0].x,y = a[0].y;
// int cnt = 1;
for(int i=1;i=a[i].x) y = max(a[i].y,y);
else{
res.push_back({x,y});
x = a[i].x;
y = a[i].y;
// cnt++;
}
}
res.push_back({x,y});
cout<