whale-quant 学习 part4：量化选股策略

为什么需要选股

在经济学的有效市场理论模型中，一般可以根据有效性将证券市场分为四种类型：无效市场、弱式有效市场、半强式有效市场和强式有效市场。

• 在无效市场中，当前股价未反映历史价格信息，那么未来的价格将进一步对过去的价格信息作出反应，可以利用过去的价格信息分析未来股价的变化倾向，从中获利。

• 在弱式有效市场中，股价的技术分析失去作用。基本面分析还可以帮助投资者获取超额利润。

• 在半强式有效市场中，基本面分析失效。 （基本面分析是利用公司的盈利、股利前景、未来利率的预期以及公司的风险评估等公开信息来决定适当的股票价格。此时通过内幕消息仍然能够帮助投资者获益。）

• 在强式有效市场中，证券价格已经充分反映了所有的信息，包括公开的和内幕的信息，那么投资者就只能采取保守策略，获得市场平均水平的收益。

以上几种划分只是经济学家为研究方便而构建出的理想情况，在现实中未必能找到完美的对应，但是有效市场理论很好地帮助我们定义了证券市场的有效性以及这种有效性的来源：如果市场能够越好地将历史价格信息、基本面和内幕消息反映到股票价格上，那么该市场就越是有效。

2013年诺贝尔经济学奖得主的研究表明，在短期看来市场是无效的，而长期来看市场是有效的，人们无法预测股票和债券在三五天内的价格，却可以预测更长期例如在未来三年至五年内的走势。在短期内，交易极易受到情绪和非理性因素影响，这些非理性的交易者会给市场带来噪音，从而促使股票价格偏离其实际价值，从而展示出证券市场无效性的一面；而从长期来看，由于大部分投资人都是理性的，便展示出证券市场有效性的一面。(美国经济学家尤金·法马、拉尔斯·彼得·汉森和罗伯特·席勒)

证券市场在短期内的无效会使得一些有价值的股票出现较低的价格，而长期的有效会使得这些低价的股票回归到其应有的高价格，精准地选取到这些股票就能使交易者在这种低买高卖中获取超额收益。量化交易就是尽量摆脱情绪对交易造成的消极影响，更客观地帮助投资者选取可能带来超额收益的股票。

单/多因子选股模型

效用模型与风险模型

效用函数
在经济学中，为了简化问题，假设每一个人都有一个$u(x)$，它的输入是一个财富总额，输出是这么多的财富可以给这个人带来多少效用。效用，简单来讲就是指金钱和物质给一个人带来的在生活中的满足感和便利性。每个人的效用函数是不一样的，但是抛开个体差异，一般来讲，大多数人的效用函数都满足两个性质。

• 性质1：如果$x\le y$,那么$u(x)\le u(y)$。即钱多总比钱少好
• 性质2：如果$d\ge 0$，并且$x\le y$ ，那么$$u(x+d)-u(x)\ge u(y+d)-u(y)$$ 即给两个人同样数额的钱，其中较穷的那个人获得的效用更多。效用函数符合该性质的投资者被称为风险厌恶者。

期望效用假说
期望效用假说：如果一个投资者的效用函数$u$，面对$n$种选项，并且这些选项的财富值结果可以用随机变量$X1,X2,X3,...,X3,Xn$ 表示 ，那么该投资者会选择$E[u(X)]$最大的那个选项(追求最大期望值)

损失厌恶
损失厌恶 行为经济学概念 指人们对于损失的敏感程度远远大于他们对同等数额的收益的敏感度。
即，假设投资A的回报可以用随机变量$X$表示，这项投资的回报预期是$E[X]$,再假设一个投资者具备效用函数$u$ 且现有财富是$x0$那么，该投资者投资于$A$后的财富值可以用随机变量$x0+X$表示，进行该投资的效用是$u(x0+X)$，此项投资给他的额外效用是 $u(x0+X)-u(x0)$。因此，投资A带给投资者的预期效用收益是$E[u(x0+X)-u(x0)]$ 若$E[X]=0$,则该投资为零收益投资，那么$E[u(x0+X)]\le u(x0)$
分散风险
经济学中的风险指未来的不确定性(在概率学中看来一个随机变量分布越散开，其确定性就越低) 所以，一个简易的衡量风险的标准，就是收益变量的标准差${\sigma }_X$ 一般来讲，在保持$E[X]$不变的情况下，我们希望${\sigma }_X$越低越好
对投资者的假设
对于一个投资者，如果任意两个投资回报率的随机变量$X$和$Y$满足$E[X]\ge E[Y]$ 且${\sigma }_X<{\sigma }_Y$ (预期收益更大但风险更小)。投资者会选择$X$，因为投资者是理性的

MPT 模型

金融资产配置的目标是将投资资金合理地分配在多种资产上，在将风险控制在一定范围内的同时把收益率最大化。
MPT 的核心思想是以最小化标准差并最大化预期收益为目标来进行资产配置，有时也称为均值-方差分析(Mean-Variance Analysis)，是金融经济学的一个重要基础理论。
模型和假设
假设市场上有n种不同的金融资产(可狭义理解为股票) $1,2,...n$ 对于某一资产 $i$ 用$r_i$ 表示该资产的收益率的随机变量，$E[r_i]$表示收益率的预期，${\sigma }_i$ 表示 $r_i$的标准差。
将市场上所有收益率方差大于0的资产称为 风险资产 将收益率没有不确定性的资产称为 无风险资产，且假设市场上所有无风险资产的收益率是一样的，称为无风险利率$r_f$
一个风险资产配置 P 是由风险资产按照某个权重比例组成的，每一个资产i在P中的权重是$w_i$ 满足${\sum }_{i=1}^n{w}_i=1$ 假设市场完全开放，且可以无限制的买多或卖空，因此$w_i$ 可以是任何实数

根据单个资产的收益率，可以计算资产配置P的收益变量的一些性质。资产组合收益率的随机变量$r_P={\sum }_{i=1}^n{w}_i{r}_i$ 其预期收益是$E[r_P]=E[{\sum }_{i=1}^n{w}_i{r}_i]={\sum }_{i=1}^{n}E[r_i]$ 方差是$Var(r_P)=E[r_P-E[r_p]]={\sum }_{i=1}^n{\sum }_{j=1}^n{w}_i{w}_{j}Cov(r_i,r_j)$
有效前沿

现在，我们固定预期收益，然后拥有该预期收益，并且标准差最小的资产组合。也就是说，对于任意一个预期收益值$\mu$ 找到一个配置权重$w=(w_1,w_2,....w_n)$ 定义的资产配置P，要求P的预期收益率为$\mu$ 且 在所有可配置出的预期收益为 $\mu$的组合中，P的方差是最小的 以最优化问题表示：
$$最小化Var(r_P)=E[r_P-E[r_P]]=\sum _{i=1}^n\sum _{j=1}^n{w}_i{w}_{j}Coc(r_i,r_j)$$

$$满足E[r_P]=E[\sum _{i=1}^n{w}_i{r}_i]=\sum _{i=1}^n{w}_{i}E[r_i]=\mu ,\sum _{i=1}^n{w}_i=1$$

这个问题的最佳解用 Lagrange 乘子的方法可以找出。对于每一个值 μ，我们求得一个风险资产配置P，满足$E[r_P]=\mu$ 且${\sigma }_P$是最小的。将这些最优解画成图，在标准差-预期的坐标上得到一条抛物线。根据计算所用到的资产的信息不同，这根曲线会不尽相同，但基本上遵循这个形状。

此曲线被称为 有效前沿 也称为马科维兹子弹 有效前沿存在一个波动率最小的位置A，并且在这个点以上的位置才是真正有效的；我们是固定预期收益算得的最低风险而得到的这条曲线，如果再固定风险并选择最大的预期收益，则会筛选掉有效前沿的下半部分。所以，很多时候人们所说的“有效前沿”会特指上半部分。

夏普比率
有效前沿左侧的区域是通过风险资产无法配置出的。但是如果把无风险资产加入资产配置，那么左侧的一些位置是可以获取的。
选择有效前沿上的一个资产配置P，并选择比例$\alpha \ge 0$,将本金的$\alpha$配置P，并将$1-\alpha$配置于无风险资产。如果$\alpha \le 1$ 那么$1-\alpha \ge 0$ (将$1-\alpha$倍的本金存入银行或买入债券，获取那部分的无风险利率)如果$\alpha \ge 1$ 那么$1-\alpha \le 0$(我们贷款本金 $\alpha -1$倍的资金，支付无风险利率，并用贷款连同本金一并配置P) 这样，以$\alpha$为系数，使用P和无风险资产配制出一个组合，我们将它的收益随机变量记为$r_{\alpha }$ 得一下计算:
$$E[r_{\alpha }]=E[\alpha r_P+(1-\alpha )r_f]=\alpha E[r_P]+(1-\alpha )r_f$$
$${\sigma }_{\alpha }=\sqrt{Var(\alpha r_P+(1-\alpha )r_f)}=\alpha {\sigma }_P$$
以上配置组合在期望收益率-标准差曲线上表现为一条经过有效边界上一点的射线，这条线被称为资本配置线（CAL, Capital Allocation Line），线上的每一点表示一个风险资产与无风险资产组成的投资组合。

• CAL的斜率为$Sharpe(P)=\frac{E(r_P)-r_f}{{\alpha }_P}$ 报酬-波动性比率 也称为夏普比率
  夏普比率刻画了投资组合每承受一单位总风险，会产生多少超额报酬(夏普比率越高投资组合越佳，同时在给定的标准差上，夏普比率越高的CAL拥有更好的期望收益)

市场组合和资本市场线
用市场信息计算得来的有效前沿上必定有一个夏普比率最高的点M，我们将其叫做市场组合(market portfolio)。穿过M的资产配置线CAL(M)叫做资本市场线(capital market line)。资本市场线的意义在于，固定标准差，那么市场上收益预期最高的投资组合在这条线上；或者，固定预期收益，那么市场上标准差最低的投资组合在这条线上。所以，资本配置线可以直观地理解为理论上的“最佳配置线”。

CAPM 模型

资本资产定价模型（Capital Asset Pricing Model，简称CAPM）建立于MPT之上，用简单的数学公式表述了资产的收益率与风险系数 $\beta$ 以及系统性风险之间的关系。
模型假设
CAPM 假设

• 市场上所有的投资者对于风险和收益的评估仅限于对于收益变量的预期值和标准差的分析，而且所有投资者都是完全理智的
• 市场是完全公开的，所有投资者的信息和机会完全平等，任何人都可以以唯一的无风险利率无限制地贷款或借出。

为了最大化预期收益并最小化标准差，所有投资者必定选择资本市场线上的一点作为资产配置。也就是说，所有投资者都按一定比例持有现金和市场组合M。因此，M 是名副其实的“市场组合”，因为整个市场都是按照这个组合来分配资产的。所以 M 的波动性和不确定性不单单是市场组合的风险，也是整个市场的风险，叫做系统性风险(systematic risk)。
CAPM公式
CAPM 公式表示了任何风险资产的收益率和市场组合的收益率之间关系。在这个公式中，任何风险资产的收益率都可以被分为两个部分：无风险收益和风险收益（β 收益）
对于某一风险资产S，有$E[r_S]=r_f+{\beta }_S(E[r_M]-r_f)$其中$r_S$是S的收益变量，$r_M$是市场组合的收益变量，$r_f$是市场的无风险利率 ${\beta }_S=\frac{Cov(r_S,r_M)}{Var(r_M)}$是组合S对于市场风险的敏感度。$E[r_M]-r_f$是市场组合的风险收益，${\beta }_S(E[r_M]-r_f)$是资产S的风险收益，可以理解为，资产S承担${\beta }_S$倍的市场风险，所以将会得到相应倍数的风险补偿。
在CAPM中，风险组合S的预期收益是完全由它的${\beta }_S$ 决定的 与资产自己的风险 ${\sigma }_S$是没有关系的
通过CAPM公式可以推算出资产S的夏普比率和市场组合M的夏普比率的关系
$$Sharpe(S)=Corr(r_S,r_M)Sharpe(M)$$
组合S 的夏普比率等于M 的夏普比率乘以M 与 S 的相关系数。在 MPT 模型中，M 是所有风险组合中夏普比率最高的，也就是最有效的。这个公式告诉我们， S 和M 的相关性越高，S 的夏普比率就越高，收益与风险的比值也就越大。

CAPM的应用
CAPM 公式的应用在理论上是一个悖论，那是因为在 CAPM 的假设下所有投资者都持有市场组合 M，那么投资者也没有必要去单独计算每一个风险资产的收益率 ，因为他所持有的资产配置已经是最优的了。但实际上，投资者的效用标准都不一样，资产配置也大相庭径，并不存在一个一致认同的市场组合，这时 CAPM 公式就可以派上用场。在现实环境里，我们可以将一个概括市场整体的组合（比如大盘指数）作为市场组合，并以其为基准计算每个风险资产的系统性风险β。这样，我们根据对市场整体趋势的判断以及对风险控制的需要，选择适当的β进行资产配置

套利定价理论(APT)与多因子模型

套利定价理论可以被理解为CAPM的一个推广，由APT给出的定价模型与CAPM一样，都是均衡状态下的模型，不同的是：CAPM把收益单纯的归为市场变化这一个因子引起的，而APT把收益归因在不同的因子上面

APT 模型认为，套利行为是现代有效市场（即市场均衡价格）形成的一个决定因素，如果市场未达到均衡状态的话，市场上就会存在无风险套利机会，套利行为会使得市场重新回到均衡状态
APT 模型用多个因素来解释风险资产的收益，并根据无套利原则，得到风险资产均衡收益与多个因素之间存在（近似的）线性关系。也就是说，股票或者组合的预期收益率是与一组影响它们的系统性因素的预期收益率线性相关的，影响股票预期收益率的因素从CAPM 中的单一因素扩展到多个因素。多因子模型（Multiple-Factor Model, MFM）正是基于 APT 模型的思想发展出来的完整的风险模型。

现代金融理论认为，股票的预期收益是对股票持有者所承担风险的报酬，多因子模型正是对于风险—收益关系的定量表达，不同因子代表不同风险类型的解释变量。多因子模型定量刻画了股票预期收益率与每个因子之间的线性关系，可以表示为
$$\widetilde{r_j}=\sum _{k=1}^K{X}_{jk}\ast \widetilde{f_k}+\widetilde{{\mu }_j}$$
其中 $X_{jk}$是股票j在因子k上的因子载荷，$\widetilde{f_k}$是因子k的因子收益，$\widetilde{{\mu }_j}$是股票j的残差收益率
多因子模型常用三类因子：技术(动量、换手率、量比、波动等)、宏观(GDP增长、工业增加值、CPI、利率、M1、M2等)、基本面(估值、营收、净利润、负债)

常见的因子分类

基于日频率数据的量化因子构建

日频初始量化指标计算过程
常用日频基础数据列表




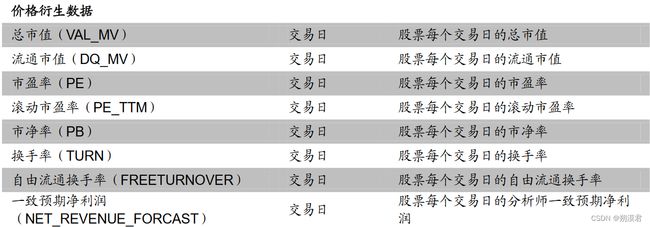
日频因子的初始量化指标计算过程便是通过设置不同参数提取上述指标的过程。
量化因子计算的常见操作过程为，处理以交易日为时间序列、不同标的为截面维度的数据类型。上表中不同周期类型的数据，除交易日类型的价量数据、价格衍生数据外，其他基本面数据，如财报数据、不定期公告数据，均可以利用最近数值填充法，将其处理为以交易日为时间序列的面板数据。
日频量化指标计算算子

利用计算机语言表达量化计算过程的递归逻辑

基于高频数据的量化因子构建

随着传统量化选股方式的广泛应用，经典日频因子的效果逐渐降低，并逐渐转化为风险因子。 因此，除利用自动因子生成方式，尽可能挖掘传统基础数据的有效信息外，引入新的量化因子数据源是提供组合 ALPHA 的重要方式。自 2010 年交易所推出LEVEL2 行情源以来，透过描述市场成交细节的日内高频行情信息，分析、寻找价格形成的细节脉络成为构建新的 ALPHA 因子的重要方式。 相较于日频数据，高频数据虽然拥有更高的数据密度与不同的数据结构，但就单个标的来看，依然可以将其定义为一种时间序列数据进行处理。因此，对应的因子计算过程的大体思路依然可以沿用上一节所述的量化因子计算过程这一框架。
高频初始量化指标计算过程




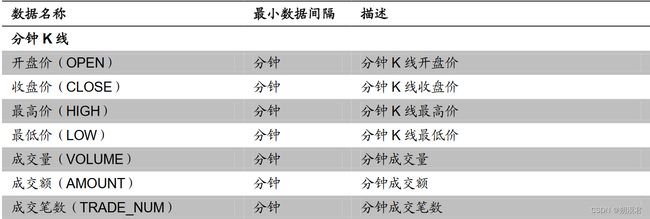
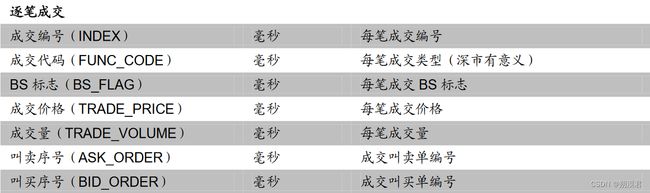
高频与日频数据间的最大差异在于不同的时间周期与数据结构。与传统的日频数据相比，除单日数据量大增外，时间单位的不整齐也是高频数据的另一重要特征。除分钟数据严格的在每个交易日的 240 分钟均有数据外，Tick 数据、逐笔数据均会因标的成交热度不同而有较大差异，其时间序列有明显的时间间隔不均匀特性。

高频量化计算算子

• 分段数据处理
• 高频数据的低频化：间隔不均匀的时间序列数据往往需要先变为均匀时间间隔的数据后，才能进一步处理
• 计算时间窗应当避免跨交易日

常见的因子有效性检验方法

风险管理|风险和收益中的取与舍
从学术角度，P值能够帮助判别因子有效性

行业与市值中性化

在股票市场中，投资者常常利用多种因子来预测股票的未来收益，并根据预测结果制定投资策略。然而，这些因子的有效性往往会受到股票市值、行业归属、投资风格等因素的影响。==比如，某个因子对于大市值的股票可能非常有效，而对小市值的股票则效果较弱；同样，某个因子在某个行业中可能非常有用，但在另一个行业中可能并不适用。==因此，我们需要对因子进行处理，剔除掉因子中可能包含的其他因素，使得我们的因子更加纯粹，更能反映其自身的信息。

因子中性化，也被称为正交化，是一种剔除已有常见因子影响的方法。在实际操作中，我们一般只考虑市值和行业这两个方面的影响，这两种影响分别称为市值中性化和行业中性化。

市值中性化是一种常用的因子中性化方法，其主要目标是剔除股票市值对因子影响，从而得到更纯粹的因子值。这种方法尤其适用于处理连续性数据。在具体操作中，市值中性化通常通过对市值取对数然后进行线性回归的方法来实现。我们通常设定一个模型，如下式所示：
$$Y=\beta .ln(MarketValue)+\alpha +\epsilon$$
其中：

• $Y$ 是我们关注的因子
• $MarketValue$ 是股票的市值
• $\beta$和$\alpha$是回归系数，需要通过数据来估计
• $\epsilon$ 是回归残差，代表在控制了市值影响之后，因子的真实值
  在进行回归分析后，得到的$\epsilon$就是市值中性化后的因子，这个因子已经剔除了市值的影响，因此能更好地反映其他因素的影响。
  python示例如下：

import numpy as np
import pandas as pd
import statsmodels.api as sm

# 假设我们有一个包含市值因子和收益的数据框 DataFrame
# 数据框的列包括：'日期'、'股票代码'、'市值'、'收益'等

# 假设我们已经从数据源加载了数据，存储在变量 data 中

# 选择所需的列
data = data[['日期', '股票代码', '市值', '收益']]

# 根据日期进行分组
groups = data.groupby('日期')

# 定义一个函数来执行市值中性化
def market_neutralize(group):
    # 提取市值和收益的数据列
    market_cap = group['市值']
    returns = group['收益']

    # 添加截距项
    X = sm.add_constant(market_cap)

    # 执行线性回归，拟合收益率与市值的关系
    model = sm.OLS(returns, X)
    results = model.fit()

    # 提取回归系数
    beta = results.params['市值']

    # 计算市值中性化后的收益
    neutralized_returns = returns - beta * market_cap

    # 将市值中性化后的收益添加到数据框中
    group['市值中性化收益'] = neutralized_returns

    return group

# 对每个日期的数据进行市值中性化
neutralized_data = groups.apply(market_neutralize)

行业中性化是为了剔除因子在不同行业间的差异，得到真正意义上的因子收益，使得因子在所有行业之间的表现更加稳定。行业中性化更多针对离散数据，具体来说，行业中性化可以通过两种方法进行：行业均值做差和回归取残差

• 行业均值做差 ：通过将股票按照行业进行分组，计算每个行业分组的因子行业均值，然后将每个股票的因子值减去对应的行业的因子的均值，得到的差值就是该因子在行业中性化后的中性值。
  假设我们要计算因子$Y$的行业中性化值，对股票$i$所在的行业$Industr{y}_i$ 该方法可以用以下公式表示：
  $${\epsilon }_i=Y_i-{\bar{Y}}_{Industr{y}_i}$$
  • $Y_i$是股票i的因子值
  • ${\bar{Y}}_{Industr{y}_i}$是股票i所在行业的因子均值
  • ${\epsilon }_i$就是股票i的行业中性化后的因子值
• 回归取残差
  对于离散数据的回归法使用哑变量线性回归法。假设当前股票中一共有n个行业，那么就有n个哑变量。原理和结果与行业均值做差法一样，可以用以下公式表示：

$$Y_i=\sum _{j=1}^{n}Industr{y}_{ij}\ast {\beta }_j+\alpha +{\epsilon }_i$$
其中：

• $Industr{y}_{ij}$是股票i所在行业的哑变量(如果股票i属于行业j，则$Industr{y}_{ij}=1$,否则$Industr{y}_{ij}=0$)
• ${\beta }_j$是行业j的回归系数
• $\alpha$是截距项
• ${\epsilon }_i$是股票i行业中性化后的因子值
  行业中性化的目标是找到因子$Y$和行业哑变量之间的关系，然后将行业因素的影响从因子$Y$中剔除，得到真正的因子收益$\epsilon$

python多因子选股策略实践

多因子选股模型是一个用来选择股票投资组合的策略，它考虑了多个与预期收益相关的因子。这种模型的理念基于这样的理论：单一因子可能无法全面捕捉到市场的所有变化，而多个因子的组合可以提供更全面、更稳定的预测。 其核心思想是通过多个因子的组合来选择股票，因子可以通过历史数据来计算，然后用来预测未来的股票表现，以期获取更全面、更稳定的预测。这些因子可以包括基本面因子、技术分析因子、宏观经济因子等。例如：

• 基本面因子：包括市盈率（PE）、市净率（PB）、营业收入增长率等
• 技术分析因子：包括动量（Momentum）、波动率（Volatility）等
• 宏观经济因子：包括利率、通货膨胀率等

在实现多因子选股模型时，需要进行以下步骤：
1、确定目标和约束条件：明确多因子模型要达到的投资目标收益率、风险水平等要求。同时考虑实际的投资约束,例如组合数目限制、行业比例限制等。

2、选择因子并计算：根据目标和约束条件,选择合适的股票因子,如PE, PB等。收集数据计算得到每只股票的各因子值。

3、异常值处理：检查数据中的异常值和错报数据,进行处理和滤除,保证因子值的质量。

4、因子标准化：因为不同因子的取值范围差异很大,需要进行标准化处理,例如去均值和缩放等。

5、确定因子权重：根据因子的重要性给予不同权重,通常通过统计方法比如主成分分析来确定。

6、构建多因子模型：结合因子值和权重,建立多因子评分模型,得到各股票的综合评分。

7、股票筛选和组合优化：根据评分进行股票筛选,并进行组合优化,获得符合目标和约束条件的优化组合。

8、回测和调整模型：使用历史数据回测多因子模型的效果,根据结果进行调整和改进。
示例：

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

# 读取和准备数据
df = pd.read_csv('stock_data.csv')
X = df[['PE', 'PB', 'ROE']] # 特征因子
y = df['Returns'] # 目标变量

# 拆分训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 标准化处理
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 构建线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)

# 查看模型系数,确定因子权重
print('Factor weights:', model.coef_)

# 使用模型预测测试数据的收益
y_pred = model.predict(X_test)

# 创建一个DataFrame来存储股票的预测收益
predicted_returns = pd.DataFrame({
    'Stock': X_test.index,
    'Predicted return': y_pred
})

# 根据预测的收益选择股票
selected_stocks = predicted_returns[predicted_returns['Predicted return'] > 0.1]

print('Selected stocks:', selected_stocks)

参考

Datawhale 202401 whale-quant 开源学习