混淆矩阵、准确率、查准率、查全率、DSC、IoU、敏感度的计算

1.背景介绍

在训练的模型的时候，需要评价模型的好坏，就涉及到混淆矩阵、准确率、查准率、查全率、DSC、IoU、敏感度的计算。

2、混淆矩阵的概念

所谓的混淆矩阵如下表所示：

TP:真正类，真的正例被预测为正例

FN:假负类，样本为正例，被预测为负类

FP:假正类 ，原本实际为负，但是被预测为正例

TN:真负类，真的负样本被预测为负类。

从混淆矩阵当中，可以得到更高级的分类指标：Accuracy（准确率），Precision（查准率），Recall（查全率），Specificity（特异性），Sensitivity（灵敏度）。

3. 常用的分类指标

3.1 Accuracy（准确率）

不管是哪个类别，只要预测正确，其数量都放在分子上，而分母是全部数据量。常用于表示模型的精度，当数据类别不平衡时，不能用于模型的评价。

3.2 Precision（查准率）

即所有预测为正的样本中，预测正确的样本的所占的比重。

3.3  Recall（查全率）

真实的为正的样本，被正确检测出来的比重。

3.4 Specificity（特异性）

特异性指标，也称 负正类率（False Positive Rate, FPR），计算的是模型错识别为正类的负类样本占所有负类样本的比例，一般越低越好。

3.5 DSC（Dice coefficient）

Dice系数，是一种相似性度量，度量二进制图像分割的准确性。

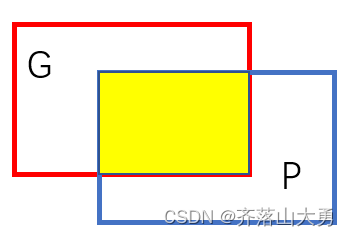
如图所示红色的框的区域时Groudtruth，而蓝色的框为预测值Prediction。

3.6 IoU（交并比）

3.7 Sensitivity（灵敏度）

反应的时预测正确的区域在Groundtruth中所占的比重。

4. 计算程序

ConfusionMatrix 这个类可以直接计算出混淆矩阵

from collections import defaultdict, deque
import datetime
import time
import torch
import torch.nn.functional as F
import torch.distributed as dist
import errno
import os


class SmoothedValue(object):
    """Track a series of values and provide access to smoothed values over a
    window or the global series average.
    """

    def __init__(self, window_size=20, fmt=None):
        if fmt is None:
            fmt = "{value:.4f} ({global_avg:.4f})"
        self.deque = deque(maxlen=window_size)
        self.total = 0.0
        self.count = 0
        self.fmt = fmt

    def update(self, value, n=1):
        self.deque.append(value)
        self.count += n
        self.total += value * n

    def synchronize_between_processes(self):
        """
        Warning: does not synchronize the deque!
        """
        if not is_dist_avail_and_initialized():
            return
        t = torch.tensor([self.count, self.total], dtype=torch.float64, device='cuda')
        dist.barrier()
        dist.all_reduce(t)
        t = t.tolist()
        self.count = int(t[0])
        self.total = t[1]

    @property
    def median(self):
        d = torch.tensor(list(self.deque))
        return d.median().item()

    @property
    def avg(self):
        d = torch.tensor(list(self.deque), dtype=torch.float32)
        return d.mean().item()

    @property
    def global_avg(self):
        return self.total / self.count

    @property
    def max(self):
        return max(self.deque)

    @property
    def value(self):
        return self.deque[-1]

    def __str__(self):
        return self.fmt.format(
            median=self.median,
            avg=self.avg,
            global_avg=self.global_avg,
            max=self.max,
            value=self.value)


class ConfusionMatrix(object):
    def __init__(self, num_classes):
        self.num_classes = num_classes
        self.mat = None

    def update(self, a, b):
        n = self.num_classes
        if self.mat is None:
            # 创建混淆矩阵
            self.mat = torch.zeros((n, n), dtype=torch.int64, device=a.device)
        with torch.no_grad():
            # 寻找GT中为目标的像素索引
            k = (a >= 0) & (a < n)
            # 统计像素真实类别a[k]被预测成类别b[k]的个数(这里的做法很巧妙)
            inds = n * a[k].to(torch.int64) + b[k]
            self.mat += torch.bincount(inds, minlength=n**2).reshape(n, n)

    def reset(self):
        if self.mat is not None:
            self.mat.zero_()

    def compute(self):
        h = self.mat.float()
        # 计算全局预测准确率(混淆矩阵的对角线为预测正确的个数)
        acc_global = torch.diag(h).sum() / h.sum()
        # 计算每个类别的准确率
        acc = torch.diag(h) / h.sum(1)
        # 计算每个类别预测与真实目标的iou
        iu = torch.diag(h) / (h.sum(1) + h.sum(0) - torch.diag(h))
        return acc_global, acc, iu

    def reduce_from_all_processes(self):
        if not torch.distributed.is_available():
            return
        if not torch.distributed.is_initialized():
            return
        torch.distributed.barrier()
        torch.distributed.all_reduce(self.mat)

    def __str__(self):
        acc_global, acc, iu = self.compute()
        return (
            'global correct: {:.1f}\n'
            'average row correct: {}\n'
            'IoU: {}\n'
            'mean IoU: {:.1f}').format(
                acc_global.item() * 100,
                ['{:.1f}'.format(i) for i in (acc * 100).tolist()],
                ['{:.1f}'.format(i) for i in (iu * 100).tolist()],
                iu.mean().item() * 100)


class DiceCoefficient(object):
    def __init__(self, num_classes: int = 2, ignore_index: int = -100):
        self.cumulative_dice = None
        self.num_classes = num_classes
        self.ignore_index = ignore_index
        self.count = None

    def update(self, pred, target):
        if self.cumulative_dice is None:
            self.cumulative_dice = torch.zeros(1, dtype=pred.dtype, device=pred.device)
        if self.count is None:
            self.count = torch.zeros(1, dtype=pred.dtype, device=pred.device)
        # compute the Dice score, ignoring background
        pred = F.one_hot(pred.argmax(dim=1), self.num_classes).permute(0, 3, 1, 2).float()
        dice_target = build_target(target, self.num_classes, self.ignore_index)
        self.cumulative_dice += multiclass_dice_coeff(pred[:, 1:], dice_target[:, 1:], ignore_index=self.ignore_index)
        self.count += 1

    @property
    def value(self):
        if self.count == 0:
            return 0
        else:
            return self.cumulative_dice / self.count

    def reset(self):
        if self.cumulative_dice is not None:
            self.cumulative_dice.zero_()

        if self.count is not None:
            self.count.zeros_()

    def reduce_from_all_processes(self):
        if not torch.distributed.is_available():
            return
        if not torch.distributed.is_initialized():
            return
        torch.distributed.barrier()
        torch.distributed.all_reduce(self.cumulative_dice)
        torch.distributed.all_reduce(self.count)

分类指标的计算

import torch

# SR : Segmentation Result
# GT : Ground Truth

def get_accuracy(SR,GT,threshold=0.5):
    SR = SR > threshold
    GT = GT == torch.max(GT)
    corr = torch.sum(SR==GT)
    tensor_size = SR.size(0)*SR.size(1)*SR.size(2)*SR.size(3)
    acc = float(corr)/float(tensor_size)

    return acc

def get_sensitivity(SR,GT,threshold=0.5):
    # Sensitivity == Recall
    SR = SR > threshold
    GT = GT == torch.max(GT)

    # TP : True Positive
    # FN : False Negative
    TP = ((SR==1)+(GT==1))==2
    FN = ((SR==0)+(GT==1))==2

    SE = float(torch.sum(TP))/(float(torch.sum(TP+FN)) + 1e-6)     
    
    return SE

def get_specificity(SR,GT,threshold=0.5):
    SR = SR > threshold
    GT = GT == torch.max(GT)

    # TN : True Negative
    # FP : False Positive
    TN = ((SR==0)+(GT==0))==2
    FP = ((SR==1)+(GT==0))==2

    SP = float(torch.sum(TN))/(float(torch.sum(TN+FP)) + 1e-6)
    
    return SP

def get_precision(SR,GT,threshold=0.5):
    SR = SR > threshold
    GT = GT == torch.max(GT)

    # TP : True Positive
    # FP : False Positive
    TP = ((SR==1)+(GT==1))==2
    FP = ((SR==1)+(GT==0))==2

    PC = float(torch.sum(TP))/(float(torch.sum(TP+FP)) + 1e-6)

    return PC

def get_F1(SR,GT,threshold=0.5):
    # Sensitivity == Recall
    SE = get_sensitivity(SR,GT,threshold=threshold)
    PC = get_precision(SR,GT,threshold=threshold)

    F1 = 2*SE*PC/(SE+PC + 1e-6)

    return F1

def get_JS(SR,GT,threshold=0.5):
    # JS : Jaccard similarity
    SR = SR > threshold
    GT = GT == torch.max(GT)
    
    Inter = torch.sum((SR+GT)==2)
    Union = torch.sum((SR+GT)>=1)
    
    JS = float(Inter)/(float(Union) + 1e-6)
    
    return JS

def get_DC(SR,GT,threshold=0.5):
    # DC : Dice Coefficient
    SR = SR > threshold
    GT = GT == torch.max(GT)

    Inter = torch.sum((SR+GT)==2)
    DC = float(2*Inter)/(float(torch.sum(SR)+torch.sum(GT)) + 1e-6)

    return DC

参考文献：

混淆矩阵的概念-CSDN博客