1.25学习总结
今天学习了二叉树,了解了二叉树的创建和遍历的过程
今天所了解的遍历过程主要分为三种,前序中序和后序,都是DFS的想法
前序遍历:先输出在遍历左节点和右节点(输出->左->右)
中序遍历:先遍历左节点,再输出和遍历右节点(左->输出->右)
后序遍历:先遍历左节点和右节点,最后再输出(左->右->输出)
#define TElemType char
typedef struct BiNode{
TElmeType data;//数据
struct BiNode *left,*right;//节点的左右指针
}BiNode,*BiTree;
void preOrderTraverse(BiTree T)
{
if (T==NULL)return ;
printf("%c",T->data);
preOrderTraverse(T->left);
preOrderTraverse(T->right);
//前序遍历中-左-右,先输出,再遍历左和右
}
void InOrderTraverse(BiTree T)
{
if (T==NULL)return ;
//中序遍历左-中-右
InOrderTraverse(T->left);//先遍历左节点
cout<data<right);
}
void PostOrderTraverse(BiTree T)
{
if (T==NULL)return ;
//后序遍历左右中
PostOrderTraverse(T->left);
PostOrderTraverse(T->right);
cout<data<>x;
if (x=='*')
{
T=NULL;
return;
}
*T=new BiNode;
//T=(BiNode*)malloc(sizeof (BiNode));
*T->data=x;
CreatTree(&(*T)->left);
CreatTree(&(*T)->right);
}
bool isempty(BiTree T)
{
return T==NULL;
} 然后尝试了一道关于树的题目
https://www.luogu.com.cn/problem/P1087
题目描述
我们可以把由 0 和 1 组成的字符串分为三类:全 0 串称为 B 串,全 1 串称为 I 串,既含 0 又含 1 的串则称为 F 串。
FBI 树是一种二叉树,它的结点类型也包括 F 结点,B 结点和 I 结点三种。由一个长度为 2�2N 的 01 串 �S 可以构造出一棵 FBI 树 �T,递归的构造方法如下:
- �T 的根结点为 �R,其类型与串 �S 的类型相同;
- 若串 �S 的长度大于 11,将串 �S 从中间分开,分为等长的左右子串 �1S1 和 �2S2;由左子串 �1S1 构造 �R 的左子树 �1T1,由右子串 �2S2 构造 �R 的右子树 �2T2。
现在给定一个长度为 2�2N 的 01 串,请用上述构造方法构造出一棵 FBI 树,并输出它的后序遍历序列。
输入格式
第一行是一个整数 �(0≤�≤10)N(0≤N≤10),
第二行是一个长度为 2�2N 的 01 串。
输出格式
一个字符串,即 FBI 树的后序遍历序列。
输入输出样例
输入 #1复制
3 10001011
输出 #1复制
IBFBBBFIBFIIIFF
说明/提示
对于 40%40% 的数据,�≤2N≤2;
对于全部的数据,�≤10N≤10。
这道题就是先按照题目中给出的方法,不断分治找到当串的长度只有1的时候,创建节点,然后再分散开建立新的节点,为了便于得到左右节点的位置,可以设置新的函数
int ls(int p){
return p*2;
}
int rs(int p){
return p*2+1;
}等完成树的创建后,最后再一个后序遍历结束
#include
using namespace std;
char s[1024],tree[4096];
int ls(int p){
return p*2;
}
int rs(int p){
return p*2+1;
}
void build_FBItree(int p,int l,int r)
{
if (l==r)
{
if (s[r]=='1')tree[p]='I';
else tree[p]='B';
return;
}
int mid=(l+r)/2;
build_FBItree(ls(p),l,mid);
build_FBItree(rs(p),mid+1,r);
if (tree[ls(p)]=='B' && tree[rs(p)]=='B')tree[p]='B';
else if (tree[ls(p)]=='I' && tree[rs(p)]=='I')tree[p]='I';
else tree[p]='F';
}
void PostOrderTraverse(int p)
{
if (tree[ls(p)])PostOrderTraverse(ls(p));
if (tree[rs(p)])PostOrderTraverse(rs(p));
printf("%c",tree[p]);
}
int main()
{
int n;
cin>>n;
//cin>>s;
scanf("%s",s+1);
build_FBItree(1,1,strlen(s+1));
PostOrderTraverse(1);
return 0;
} 第二题是有关于搜索的
https://www.lanqiao.cn/problems/644/learning/?page=1&first_category_id=1&problem_id=644
这道题是需要找到所有的对称分割方法,可以轻松的知道,分割线一定是经过对称中心的,因此可以把起始点设置在中心对称处,然后开始向四个方向搜索,当碰到边界的时候就是一种结果
#include
using namespace std;
int ans;
bool vis[10][10];
void dfs(int x,int y)
{
if (x==0 || y==0 || x==6 ||y==6)//到达边界的时候算一种方案
{
ans++;
return;
}
int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
for (int i=0;i<4;++i)
{
int tx=x+dir[i][0],ty=y+dir[i][1];
if (!vis[tx][ty])
{
vis[tx][ty]=true;
vis[6-tx][6-ty]=true;//由于对称的关系,所以只需要访问一半的对称图形就可以了
dfs(tx,ty);
vis[tx][ty]=false;//因为需要找到所有的情况,所以需要取消标记
vis[6-tx][6-ty]=false;
}
}
return;
}
int main()
{
vis[3][3]=true;//由于对称的关系,所以一定经过中心对称点,所以就从这个点开始搜索
dfs(3,3);
cout< 题2https://www.lanqiao.cn/problems/106/learning/?page=1&first_category_id=1&problem_id=106
题目描述
考虑一种简单的正则表达式:
只由 x ( ) | 组成的正则表达式。
小明想求出这个正则表达式能接受的最长字符串的长度。
例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是: xxxxxx,长度是 6。
输入描述
一个由 x()| 组成的正则表达式。输入长度不超过 100,保证合法。
输出描述
这个正则表达式能接受的最长字符串的长度。
输入输出样例
示例
输入
((xx|xxx)x|(x|xx))xx
输出
6
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
这道题,主要用的是递归的方法,由于括号内的需要重新算,所以遇到括号就调用函数,计算括号内的值,遇到有括号就相当于出栈。
#include
using namespace std;
string s;
int pos;
int dfs()
{
int len=s.size();
int tmp=0,ans=0;
while (pos>s;
int ans=dfs();
cout< 后面是每周作业
题3:高手去散步https://www.luogu.com.cn/problem/P1294
题目背景
高手最近谈恋爱了。不过是单相思。“即使是单相思,也是完整的爱情”,高手从未放弃对它的追求。今天,这个阳光明媚的早晨,太阳从西边缓缓升起。于是它找到高手,希望在晨读开始之前和高手一起在鳌头山上一起散步。高手当然不会放弃这次梦寐以求的机会,他已经准备好了一切。
题目描述
鳌头山上有 �n 个观景点,观景点两两之间有游步道共 �m 条。高手的那个它,不喜欢太刺激的过程,因此那些没有路的观景点高手是不会选择去的。另外,她也不喜欢去同一个观景点一次以上。而高手想让他们在一起的路程最长(观景时它不会理高手),已知高手的穿梭机可以让他们在任意一个观景点出发,也在任意一个观景点结束。
输入格式
第一行,两个用空格隔开的整数 �n 、 �.m. 之后 �m 行,为每条游步道的信息:两端观景点编号、长度。
输出格式
一个整数,表示他们最长相伴的路程。
输入输出样例
输入 #1复制
4 6 1 2 10 2 3 20 3 4 30 4 1 40 1 3 50 2 4 60
输出 #1复制
150
说明/提示
对于 100%100% 的数据:�≤20n≤20,�≤50m≤50,保证观景点两两之间不会有多条游步道连接。
思路:这道题可以用图的想法,一个地点可以通向不同的地方,并且是没有方向限制的,因为题目需要我们求最大的距离,所以我们可以建立一个二维数组,那么两个不同的桥就相当于它的坐标,所包含的值就是他们之间的距离,最后再搜索一下
#include
using namespace std;
int vis[25],a[60][60];
int ans,maxn,m,n;
void dfs(int k,int sum)
{
ans=max(ans,sum);
for (int i=1;i<=n;++i)
{
if (!vis[i] && a[k][i]>0)//判断能不能走
{
vis[i]=1;//目的地打上标记
dfs(i,sum+a[k][i]);
vis[i]=0;
}
}
return ;
}
int main()
{
cin>>n>>m;
for (int i=0;i>x>>y>>s;
a[x][y]=s;
a[y][x]=s;
}
for (int i=1;i<=n;++i)
{
vis[i]=1;
dfs(i,0);
maxn=max(ans,maxn);
memset(vis,0,sizeof(vis));//清空标记数组
}
cout< 接水问题https://www.luogu.com.cn/problem/P1190
题目描述
学校里有一个水房,水房里一共装有 �m 个龙头可供同学们打开水,每个龙头每秒钟的供水量相等,均为 11。
现在有 �n 名同学准备接水,他们的初始接水顺序已经确定。将这些同学按接水顺序从 11 到 �n 编号,�i 号同学的接水量为 ��wi。接水开始时,11 到 �m 号同学各占一个水龙头,并同时打开水龙头接水。当其中某名同学 �j 完成其接水量要求 ��wj 后,下一名排队等候接水的同学 �k 马上接替 �j 同学的位置开始接水。这个换人的过程是瞬间完成的,且没有任何水的浪费。即 �j 同学第 �x 秒结束时完成接水,则 �k 同学第 �+1x+1 秒立刻开始接水。若当前接水人数 �′n′ 不足 �m,则只有 �′n′ 个龙头供水,其它 �−�′m−n′ 个龙头关闭。
现在给出 �n 名同学的接水量,按照上述接水规则,问所有同学都接完水需要多少秒。
输入格式
第一行两个整数 �n 和 �m,用一个空格隔开,分别表示接水人数和龙头个数。
第二行 �n 个整数 �1,�2,…,��w1,w2,…,wn,每两个整数之间用一个空格隔开,��wi 表示 �i 号同学的接水量。
输出格式
一个整数,表示接水所需的总时间。
输入输出样例
输入 #1复制
5 3 4 4 1 2 1
输出 #1复制
4
输入 #2复制
8 4 23 71 87 32 70 93 80 76
输出 #2复制
163
说明/提示
【输入输出样例 #1 说明】
第 11 秒,33 人接水。第 11 秒结束时,1,2,31,2,3 号同学每人的已接水量为 1,31,3 号同学接完水,44 号同学接替 33 号同学开始接水。
第 22 秒,33 人接水。第 22 秒结束时,1,21,2 号同学每人的已接水量为 2,42,4 号同学的已接水量为 11。
第 33 秒,33 人接水。第 33 秒结束时,1,21,2 号同学每人的已接水量为 3,43,4 号同学的已接水量为 22。44 号同学接完水,55 号同学接替 44 号同学开始接水。
第 44 秒,33 人接水。第 44 秒结束时,1,21,2 号同学每人的已接水量为 4,54,5 号同学的已接水量为 11。1,2,51,2,5 号同学接完水,即所有人完成接水的总接水时间为 44 秒。
【数据范围】
1≤�≤1041≤n≤104,1≤�≤1001≤m≤100,�≤�m≤n;
1≤��≤1001≤wi≤100。
思路:由于一开始没有人接水,所以前面几个人可以立刻去接水,那么就会产生时间,接下来就需要知道剩下的孩子中,去接水所需要的最大时间,由于这题的数据量很小,所以我可以每安排一个孩子就排一次序,那么第一个一定是最先走的,所以一定是它的时间加上下一个接水的,等到所有孩子完成接水后,当前数组的最后一个时间就是所需要的最长时间
#include
using namespace std;
int main()
{
int n,m;
cin>>n>>m;
int a[10005];
int ss[10005];
for (int i=0;i>a[i];
//初始化水龙头,把最前面的m个人去接水
for (int i=0;i 题4:日志分析https://www.luogu.com.cn/problem/P1165
这道题主要就是再建立一个最大值栈,在只有第一个元素的时候,那个元素入栈,在接下来入栈的元素都要与这个最大值元素比较,如果更大就入栈,若遇到出栈指令,那么判断出栈元素和最大值栈的元素是否相等,如果相等那就都出栈
#include
using namespace std;
int main()
{
stackst;
stackmaxst;//建立最大值栈找最大值
int n;
cin>>n;
for (int i=0;i>x;
if (x==0)
{
long long y;
cin>>y;
if (st.empty())
{
maxst.push(y);//没有元素的情况下,剩余的元素就是最大值
}
else if (maxst.top() 题5:表达式括号匹配https://www.luogu.com.cn/problem/P1739
遇到左括号入栈,遇到右括号出栈,有一点特例就是,会出现开头就是右括号的情况,那么就直接输出失败
#include
using namespace std;
int main()
{
string s;
cin>>s;
int top=-1;
for (int i=0;s[i]!='@';++i)
{
if (s[i]=='(')top++;
else if (s[i]==')')top--;
if (top<-1)
{
cout<<"NO";
return 0;
}
}
if (top==-1)cout<<"YES";
else cout<<"NO";
return 0;
} 题6:约瑟夫问题https://www.luogu.com.cn/problem/P1996
循环队列,假定数到m的人要走,那么用while循坏直到队列中没有元素停止,那么如果当前报的数不是m的话,这个人出去在进去,进到队尾,反之则出队
#include
using namespace std;
int main()
{
int m,n;
cin>>m>>n;
queueque;
for (int i=1;i<=m;++i)
{
que.push(i);
}
int cnt=1;
while (!que.empty())
{
if (cnt!=n)
{
que.push(que.front());
que.pop();
cnt++;
}
else
{
cout< 题6:路障https://www.luogu.com.cn/problem/P3395
BFS和之前掉陨石很像,这个会在不同时间内放置路障,那么我们就建立一个二维数组,并且存放的是路障放置的时间(在这里,如果人走到那个位置恰好有路障,但是时间与人到那个地方时间相同的话,人是不会有事的),初始化路障好了之后,BFS一边就结束了,但这里要注意的是路障的个数是2n-2
#include
using namespace std;
int a[1005][1005];
int vis[1005][1005];
struct Queue{
int x;
int y;
int time;
}QQQ[1000000];
int main()
{
int t;
int flag=0;
cin>>t;
while (t--)
{
int n;
cin>>n;
memset(QQQ,0,sizeof(QQQ));
memset(a,0,sizeof(a));
memset(vis,0,sizeof(vis));
if (n==1)
{
cout<<"Yes"<>x>>y;
a[x][y]=i;//每个路障位置都带着时间
}
int head=0,tail=0;
QQQ[tail].x=1,QQQ[tail].y=1,QQQ[tail].time=0;
vis[1][1]=1;
tail++;
int dic[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
while (head!=tail)
{
for (int i=0;i<4;++i)
{
int tx=QQQ[head].x+dic[i][0],ty=QQQ[head].y+dic[i][1],tt=QQQ[head].time+1;
if (tx==n && ty==n && (a[tx][ty]==0||tt<=a[tx][ty]) )
{
flag=1;
break;
}
if (tx>=1 && ty>=1 &&tx<=n && ty<=n && (a[tx][ty]==0||tt<=a[tx][ty]) && !vis[tx][ty])
{
QQQ[tail].x=tx,QQQ[tail].y=ty,QQQ[tail].time=tt;
vis[tx][ty]=1;
tail++;
}
}
if (flag)break;
head++;
}
if (flag)
{
cout<<"Yes"< 题7:【模板】单调栈https://www.luogu.com.cn/problem/P5788
单调栈就是单调的栈,它需要知道第一个大于当前元素的元素的位置,这就符合单调递增栈的想法,具体的想法主要是从最后一个元素开始找,如果遇到比他大的元素,那么当前栈顶元素就出栈,这就相当于当你需要一个身高递增的队伍的时候,那么卡在中间的比前人矮的人就变成无效的人了,就可以删除
如果需要找后面第一个比自己小的元素的索引就是,单调减同理
#include
using namespace std;
int a[3000005];
int res[3000005];
int main()
{
int m;
stackst;
scanf("%d",&m);
for (int i=1;i<=m;++i)cin>>a[i];
//单调栈,从后面开始排,用案例来说,会先判断栈是否为空和是否栈内的元素要小于要进去的元素
//如果小了,那么栈内的元素就失去了价值,需要出栈
//在压入新元素之前,需要判断栈是否为空,如果是的,代表没有元素大于它或者他是最后一个元素,因此输出0
for (int i=m;i>0;--i)
{
while (!st.empty() && a[st.top()]<=a[i])st.pop();
res[i]=st.empty()?0:st.top();
st.push(i);
}
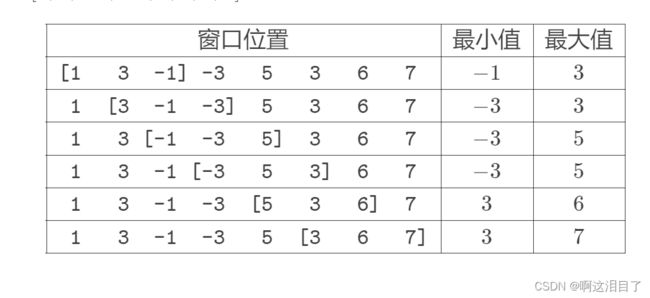
for (int i=1;i<=m;++i)cout< 题8:滑动窗口 /【模板】单调队列滑动窗口 /【模板】单调队列 - 洛谷
可以用双端队列做,想法和单调栈类似
这是找最小值的核心代码
是否需要输出是看i-k的情况,只有当i大于等于k的时候,才会出现窗口才能输出
由于需要找的是最小值,所以当当前的元素大于即将进去的元素时,需要出队,这就相当于如果有更小的元素,那么队列里面的比他小的元素都要出队,然后这个小的进去,如果这个元素比他大,那就直接进去,因为当前的最小的元素很快就会被滑动窗口淘汰
for (int i=1;i<=n;++i)
{
while (!q.empty() && q.back()>a[i])q.pop_back();
q.push_back(a[i]);
if (i-k>=1 && a[i-k]==q.front())q.pop_front();
if (i-k>=0) printf("%d ",q.front());
}最大值同理
#include
using namespace std;
int a[1000009];
int main()
{
int n,k;
scanf("%d %d",&n,&k);
dequeq;
dequep;
for (int i=1;i<=n;++i)cin>>a[i];
for (int i=1;i<=n;++i)
{
while (!q.empty() && q.back()>a[i])q.pop_back();
q.push_back(a[i]);
if (i-k>=1 && a[i-k]==q.front())q.pop_front();
if (i-k>=0) printf("%d ",q.front());
}
cout<=1 && a[i-k]==q.front())q.pop_front();
if (i-k>=0) printf("%d ",q.front());
}
} 题9:小小的埴轮兵团https://www.luogu.com.cn/problem/P7505
同理运用双端队列完成
#include
using namespace std;
dequeq;
long long tot=0;
int main()
{
int n,m,k;
cin>>n>>m>>k;
for (long long i=0;i>a;
q.push_back(a);
}
sort(q.begin(),q.end());
for (long long i=0;i>op;
if (op==3)
{
if (q.empty())cout<<0<>x;
tot+=x;
while (!q.empty())
{
long long v=q.back();
if (v+tot>k)q.pop_back();
else break;
}
}
else if (op==2)
{
long long x;
cin>>x;
tot-=x;
while (!q.empty())
{
long long v=q.front();
if (v+tot<-k)q.pop_front();
else break;
}
}
}
} 题10:表达式求值https://www.luogu.com.cn/problem/P1981
运用栈的思想,如果是先把第一个数放到栈里面,然后判断字符和数字,如果字符是乘号的话优先级比较高,那么就直接从栈里面取数字出来和这个读入的数字计算,结果放到栈里面,如果是加号的话,那么就把数字存到栈里面,最后再统一加起来
#include
using namespace std;
#define MOD 10000
int main()
{
stackst;
long long a,b;
char c;
cin>>a;
a%=MOD;
st.push(a);
while (cin>>c>>b)
{
if (c=='*')
{
long long p=(st.top()*b)%MOD;
st.pop();
st.push(p);
}
else if (c=='+')
{
st.push(b);
}
else
{
break;
}
}
long long sum=0;
while (!st.empty())
{
sum=(sum+st.top())%MOD;
st.pop();
}
cout< 题11:GITARAhttps://www.luogu.com.cn/problem/P6704
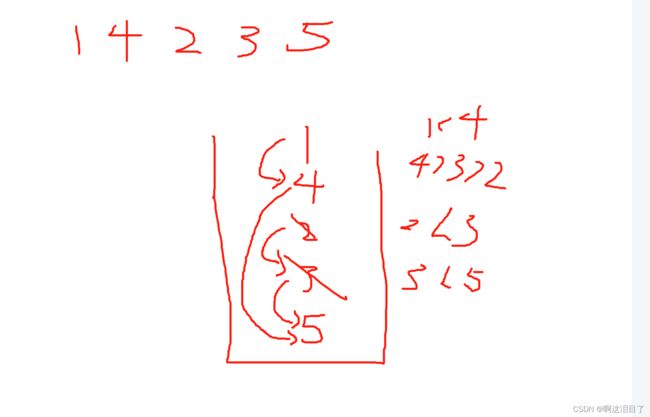
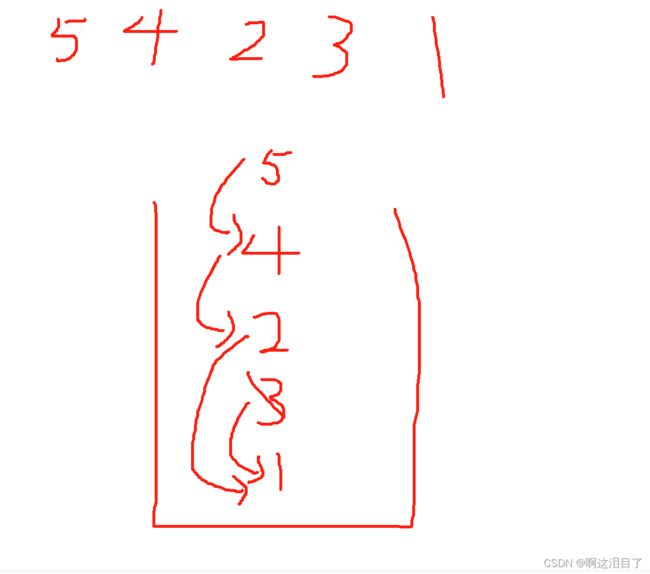
建立七个栈,读入要弹奏的,如果当前的数小于栈顶元素的数字,那么出栈,出栈也要记录个数,结束出栈后,栈内的元素都是小于等于当前元素的,所以要判断,如果栈顶元素与弹奏的元素相同的话,那么不需要再谈了,如果是小于的话,那么还需要再谈一次。
#include
using namespace std;
#define MOD 10000
int main()
{
int n,p;
cin>>n>>p;
stackst[7];
int cnt=0;
for (int i=0;i>a>>b;
while (!st[a].empty()>0&&st[a].top()>b)
{
st[a].pop();
cnt++;
}
if (!st[a].empty())
{
if (st[a].top()==b)
{
continue;
}
else
{
st[a].push(b);
cnt++;
}
}
else
{
st[a].push(b);
++cnt;
}
}
cout< 题12:验证栈序列https://www.luogu.com.cn/problem/P4387
把序列1和序列2的元素都放到两个数组里面,对于序列2需要特别的设置一个了计数器,然后就是开始遍历,把序列1中的元素压入栈中,并且同时判断,当前元素是否和序列2中相同,如果相同的话,就出栈,直到栈内没有元素为止,在继续从序列1中压入元素。元素压完后,再判断栈内是否有元素,如果没有就可以完成。
#include
using namespace std;
#define MOD 10000
int main()
{
int q;
cin>>q;
stackst1;
int a1[100005];
int a2[100005];
while (q--)
{
int n;
cin>>n;
for (int i=1;i<=n;++i)
{
cin>>a1[i];
}
for (int i=1;i<=n;++i)
{
cin>>a2[i];
}
int cnt=1;
for (int i=1;i<=n;++i)
{
st1.push(a1[i]);
while(st1.top()==a2[cnt])
{
st1.pop();
cnt++;
if (st1.empty())break;
}
}
if (st1.empty())
{
cout<<"Yes"<