双指针法|位运算|离散化|区间合并

目录

双指针算法

位运算 

离散化 

序列合并

---

 

双指针算法

题目描述：1.输入n个单词，每个单词在输入的时候按空格隔开，之后打印出每个单词且换行

#include
#include 

using namespace std;
int main()
{
	string arr;
	getline(cin, arr);
	int n = arr.size();
	for (int i = 0; i < n; ++i)
	{
		int j = i;
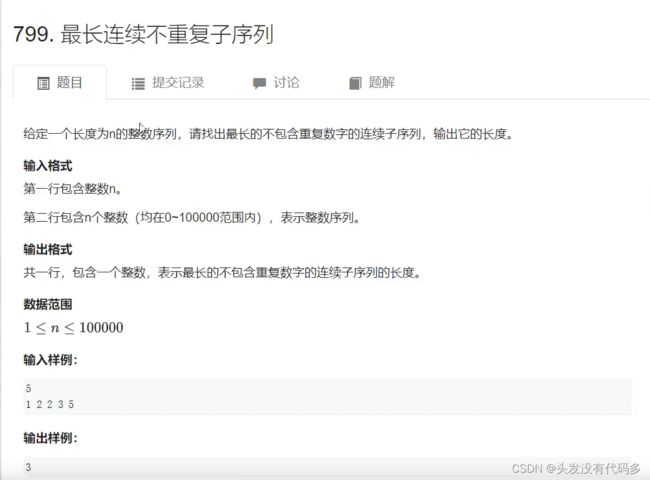
		while (arr[j] != ' '&&j

 

 习题2：最长连续不重复的子序列

#include
#include 
#include
using namespace std;
const int N = 100010;
int arr[N], s[N];
int main()
{

	int n;
	cin >> n;
	int res = 0;
	int i, j;
	for (i = 0; i < n; ++i)
		cin >> arr[i];
	for (i = 0,j = 0; i

位运算 

 lowbit(x)，返回x的最后一位1，起始就是x&-x=x&(~x+1)

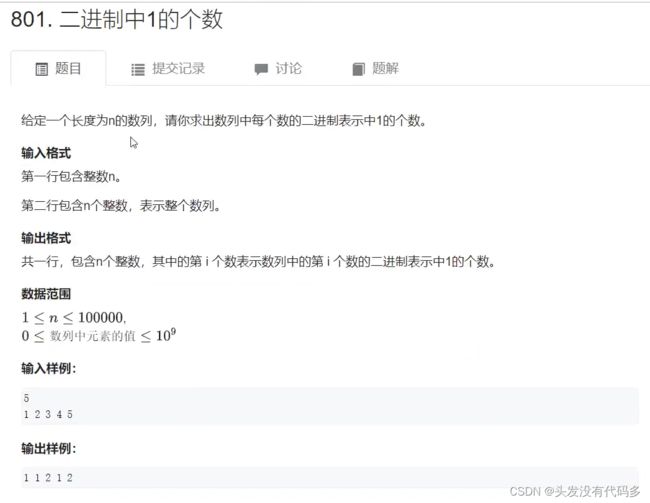
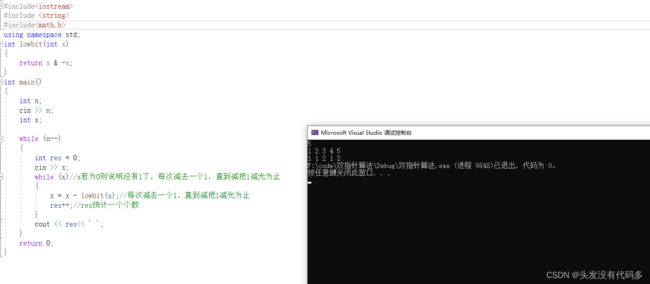
习题:求二进制中1的个数

 

#include
#include 
#include
using namespace std;
int lowbit(int x)
{
	return x & -x;
}
int main()
{
	int n;
	cin >> n;
	int x;
	
	while (n--)
	{
		int res = 0;
		cin >> x;
		while (x)//x若为0则说明没有1了，每次减去一个1，直到减把1减光为止
		{
			x = x - lowbit(x);//每次减去一个1，直到减把1减光为止
			res++;//res统计一个个数
		}
		cout << res<< ' ';
	}
	return 0;
}

 也可这样计算

int main()
{
	int n;
	cin >> n;
	int x;

	while (n--)
	{
		int res = 0;
		cin >> x;
		for (int i = 0; i < 32; ++i)
		{
			if ((x >> i) & 1 == 1)
				res++;
		}
		cout << res << ' ';
	}
	return 0;
}

离散化 

 unique函数本质是将重复的元素移动到数组的末尾，最后再将迭代器指向第一个重复元素的下标。

离散化：一般是在一个的数组中，输入x（下标），将该值映射到从1开始对应的数组

如这里要给上面数组下标为2的值离散化，离散化之后对应的下标为3

思路：先用sort函数排序，然后用unique去重，再删除重复元素，用二分查找找下标，找到返回即可 

 

 

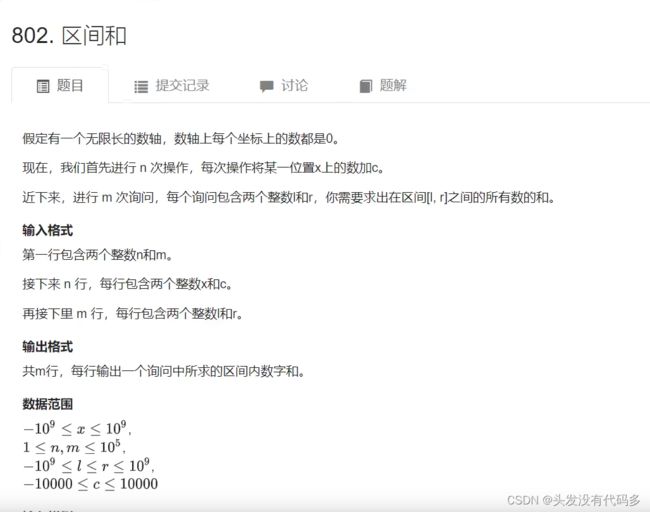
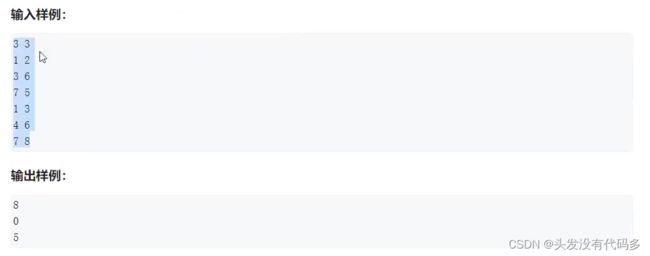
一开始数字全是0，下标为1的数+2，为3的数+6，为7的数+5，计算0-3的和，4-6的和 。7-8的和

思路：把所有加了 值的数，映射到从一开始的数组即可

有n行，所以是10的5次方个数，对于m行要输入俩个整数lr，这里又是2x10的5次方，所以总共是3x10的5次方，总共有2x10的9次方个数，但是我们只用到了3x10的5次方个数

#include
#include
#include

typedef pair PII;
const int N = 300010;
int n, m;//都代表行数n是x+c的行数,m是区间函数l,r
int a[N], s[N];//a数组用来存离散后的数x对应数字+c后的值，但这个数组是从1开始与x相对应的，若之前x是0，在这个数组中就为1，s是前缀和
vector alls;//存所有要离散化的值(这个数组里存的是下标)
vector add,query;//add是给x+c对应x,c的键值，query存放要离散化的左右区间
using namespace std;
int find(int x)
{
	int l = 0, r = alls.size()-1;
	while (l < r)
	{
		int mid = (l + r) / 2;
		if (alls[mid] >= x)
		{
			r = mid;
		}
		else
			l = mid + 1;
	}
	return r+1;//由于映射的是从1开始映射,所以给r+1。
}
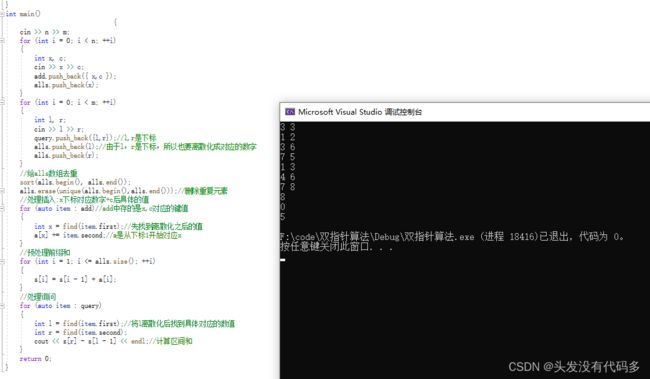
int main()
                              {
	cin >> n >> m;
	for (int i = 0; i < n; ++i)
	{
		int x, c;
		cin >> x >> c;
		add.push_back({ x,c });
		alls.push_back(x);
	}
	for (int i = 0; i < m; ++i)
	{
		int l, r;
		cin >> l >> r;
		query.push_back({l,r});//l,r是下标
		alls.push_back(l);//由于l，r是下标，所以也要离散化成对应的数字
		alls.push_back(r);
	}
	//给alls数组去重
	sort(alls.begin(), alls.end());
	alls.erase(unique(alls.begin(),alls.end()));//删除重复元素
	//处理插入:x下标对应数字+c后具体的值
	for (auto item : add)//add中存的是x,c对应的键值
	{
		int x = find(item.first);//先找到离散化之后的值
		a[x] += item.second;//a是从下标1开始对应x
	}
	//预处理前缀和
	for (int i = 1; i <= alls.size(); ++i)
	{
		s[i] = s[i - 1] + a[i];
	}
	//处理询问
	for (auto item : query)
	{
		int l = find(item.first);//将l离散化后找到具体对应的数值
		int r = find(item.second);
		cout << s[r] - s[l - 1] << endl;//计算区间和
	}
	return 0;
}

序列合并

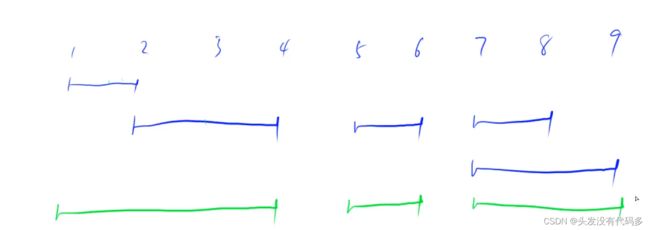
如果俩段区间有交集，就将这俩段区间合并 

绿色为合并后的区间

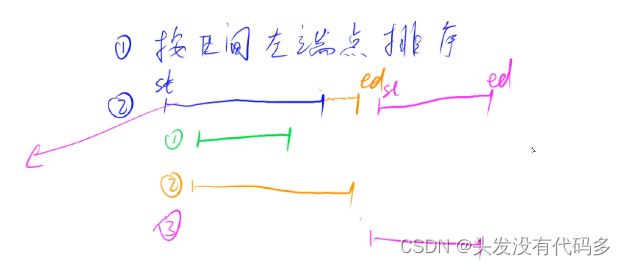
 思路：按区间左端点排序（每个区间都有自己的左端点，根据左端点的大小进行排序），扫描整个区间，扫描过程当中把有交集的区间进行合并。

不会出现红色这种情况，因为我们对左端点按照从小到大的顺序进行了排列

当第一个区间合并完之后，开始进行合并下一个区间更新start和end的位置 

 

#include
#include
#include
#include
using namespace std;
const int N = 100010;
typedef pair PII;
vector segs;//存所有的区间
void merge(vector& segs)
{
	vector res;//存放合并后的区间
	sort(segs.begin(), segs.end());//先把所有区间排序,pair排序优先以左端点排序，再以又端点排序
	int st = -2e9, ed = -2e9;//刚开始区间的大小,2*10的-9次方
	for (auto seg : segs)//从前往后扫描所有的区间
	{
		if (seg.first > ed)//如果这个区间左边的数大于上一个区间的最后一个数字，说明没有交集
		{
			if (st != -2e9)//这个区间如果不是最开始的初始区间就放入res中
			{
				res.push_back({ st,ed });
			}
				st = seg.first, ed = seg.second;//更新st和ed，让st和ed跟下一个区间进行比较
		}
		else//此时有了交集,把右端点更新成最长的哪个
		{
			ed = max(seg.second, ed);
		}
	}
	if (st != -2e9)//防止输入一个空区间
	{
		res.push_back({ st, ed });//如果不是空区间，就把最后一个区间放进去
	}

	segs = res;
}
int main()
{
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		int l, r;
		cin >> l >> r;
		segs.push_back({ l,r });
	}
	merge(segs);//进行区间合并
	cout << segs.size() << endl;
	return 0;
}