C语言与操作符相关的经典例题
目录
一道变态的面试题:不能创建临时变量(第三个变量),实现两个数的交换。
编写代码实现:求一个整数存储在内存中的二进制中1的个数。
二进制位置0或者置1
如果以下的知识点不是很清楚的可以去看这篇文章:操作符详解(上)-CSDN博客
一道变态的面试题:不能创建临时变量(第三个变量),实现两个数的交换。
这个题如果没有那个限制条件,我们一般都是创建第三个变量来处理。
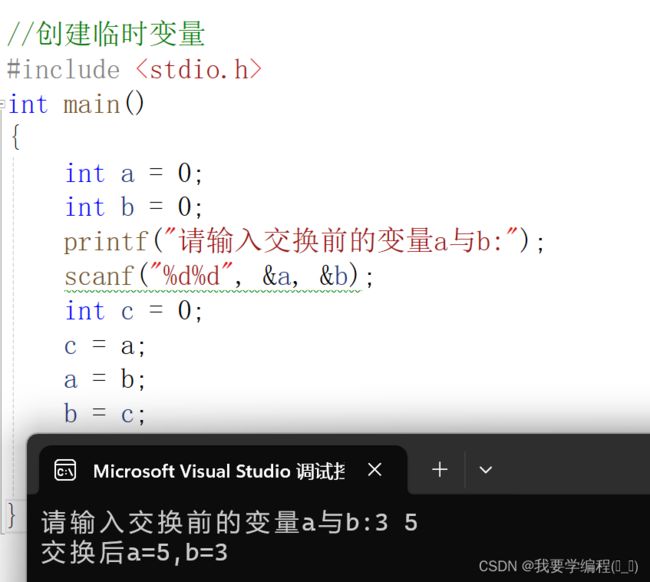
法一:
//创建临时变量
#include
int main()
{
int a = 0;
int b = 0;
printf("请输入交换前的变量a与b:");
scanf("%d%d", &a, &b);
int c = 0;
c = a;
a = b;
b = c;
printf("交换后a=%d,b=%d\n", a, b);
return 0;
} 第二种方法可能也是比较容易想到的,通过计算和来减去对应的。
法二:
//加减法
#include
int main()
{
int a = 0;
int b = 0;
printf("请输入交换前的变量a与b:");
scanf("%d%d", &a, &b);
a = a + b;
b = a - b;//a+b-b
a = a - b;//a+b-a
printf("交换后a=%d,b=%d\n", a, b);
return 0;
} 这个法二其实严格来说,是有错误的。当a和b的值接近一个整形能存储的最大值是,它们两的和就会超出这个整形的最大值,从而导致溢出的问题。
第三种方法应该只有那些大佬才能够想到。
法三:
#include
int main()
{
int a = 0;
int b = 0;
printf("请输入交换前的变量a与b:");
scanf("%d%d", &a, &b);
a = a ^ b;
b = a ^ b;//a^b^b=a
a = a ^ b;//a^b^a=b
printf("交换后a=%d,b=%d\n", a, b);
return 0;
} 这个方法涉及了一个知识点:0^a=a,a^a=0。
这个也用画图来解释一下吧:
编写代码实现:求一个整数存储在内存中的二进制中1的个数。
如果拿到这个题目的时候没思路的话,就可以先想一想十进制,求一个十进制数中1的个数,那么这个也就比较简单了,我们可以先%10,看看最后一位是否等于1,再/10赋给这个数更新一下,再%10拿到倒数第二位看看是否等于1,就这样一直%10,/10,知道最后这个/10的商为0,就可以停止了。同理,这个二进制我们也可以通过%2,/2的方法来计算。
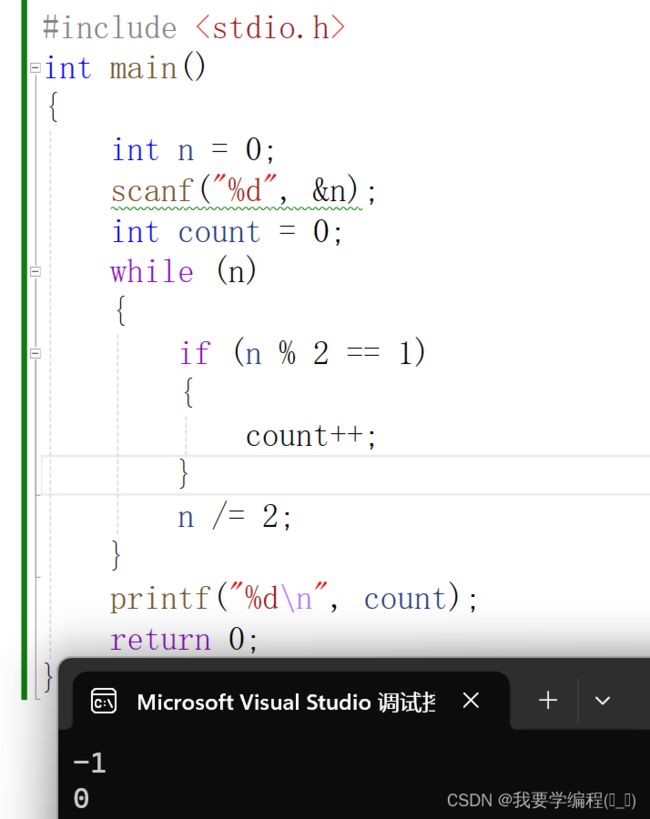
#include
int main()
{
int n = 0;
scanf("%d", &n);
int count = 0;
while (n)
{
if (n % 2 == 1)
{
count++;
}
n /= 2;
}
printf("%d\n", count);
return 0;
} 但是很遗憾的是这个代码只能求正整数,而对于负整数就不行了。
例如:当我们输入-1时,输出的却是0。我们知道-1的补码全是1,正确输出的话应该要是32。
其实这个问题还是比较好解决的,既然负数不行,那我们就把它变成无符号数,而-1的补码是32个1,那么对应的无符号数就是一个非常大的数字了。
#include
int main()
{
unsigned int n = 0;
scanf("%d", &n);
int count = 0;
while (n)
{
if (n % 2 == 1)
{
count++;
}
n /= 2;
}
printf("%d\n", count);
return 0;
} 但是如果题目要求我们用的是有符号整数,那么我们应该怎么办呢? 其实这里就可以用到那个按位与(&)操作符。这里我们就按照那个思路来想一想,当给出了一个二进制数字,我们按位与(&)上一个1,那么我们就只要看第32个比特位了(因为两个数按位与(&)的规则是对应的二进制位同为1,才是1,否则为0。而1的二进制补码,只有第32个比特位才是1,其余的都是0,那么无论什么数按位与(&)1,最终的结果是前面的第31个都是0了,只有第32个比特位还不确定。),如果那个数第32个比特位为1,那么最终的结果就是1,如果那个数第32个比特位是0,那么最终的结果就是0了。这是第32位的计算结果,如果要想知道前面的结果,就只能通过移位符来来把前面的比特位移至最后一位,再来比较。这里可能有小伙伴会有疑问,为什么不移1呢?把1一位移位的移去前面来比较。其实这个移1,也不是不可以但是比起移那个数,还是要难一些。我们移1之后就表示判断结果等于1了,而是等不等于0,如果等于0,那么就没有1,如果不等于0,那么就有1。原因我就用图来表述了:
以上就是全部的思路,接下来就用代码演示:
移输入数的位
#include
int main()
{
int n = 0;
scanf("%d", &n);
int count = 0;
int i = 0;
for (i = 1; i <= 32; i++)
{
if (n & 1 == 1)
{
count++;
}
n >>= 1;//注意这里千万不能是移i位,因为i的数字是不断增加的,而不是定值。
}
printf("%d\n", count);
return 0;
} #include
int main()
{
int n = 0;
scanf("%d", &n);
int count = 0;
int i = 0;
for (i = 0; i < 32; i++)
{
if ((n >> i) & 1 == 1)
{
count++;
}
}
printf("%d\n", count);
return 0;
}
上面这两种写法都是可以的。
移 1 的位
#include
int main()
{
int n = 0;
scanf("%d", &n);
int count = 0;
int i = 0;
for (i = 0; i < 32; i++)
{
if ((n & (1 << i)) != 0)
{
count++;
}
}
printf("%d\n", count);
return 0;
} 上面这个题目其实还能优化(属于大佬能想到的)
我就先把代码演示一下:
#include
int main()
{
int n = 0;
scanf("%d", &n);
int count = 0;
while (n)
{
n = n & (n - 1);
count++;
}
printf("%d\n", count);
return 0;
} 这个代码最难理解的就是那个 n = n & (n-1)。这个表达式可以把从右往左把最左边的1给去掉。
这个代码其实算法的体现是比较明显了 ,一般不容易想到。
二进制位置0或者置1
编写代码将n的二进制序列的第5位(从右往左的第5位)(假设第5位是0)修改为1,然后再改回0。
这个题目应该是相较前面的难度要少一点。其实我们只要在第5位异或(^)一个1,就可以了。利用异或的规则:相异为1。至于这个第5位的1是怎么来实现呢?我们只需要讲1向移4位就够了。第二部,就在第5位按位异或(^)上一个1,就可以了。因为我们前面改了第5位的数变成了1,异或相同为0。
代码实现:
#include
int main()
{
int n = 0;
scanf("%d", &n);
n ^= (1 << 4);
printf("%d\n", n);
n ^= (1 << 4);
printf("%d\n", n);
return 0;
} 代码演示:
我们上面就举了个最简单的例子0,任何一位都没有1,第5位改了之后就变成了2的4次方,等于16,第二次我们又改回来了,变成了0。