二叉树的递归算法（先序，中序，后序）以及结点数，叶子结点数和深度，树的深度

遍历二叉树的算法

递归算法

类型定义

#define MAXSIZE 100
#define MAXTSIZE 100
#define TRUE 1
#define FALSE -1
#define OK 0
#define ERROR -2

二叉树的链式存储结构

typedef struct BiNode {
    int data;
    struct BiNode *lchild, *rchild; //左右孩子指针
} BiNode, *BiTree;

​

VISIT函数

例如，

void visit(BiTree T) {
    printf("%d\t", T->data);
}

遍历的算法实现——先序遍历

Ⅰ.若二叉树为空，则空操作; Ⅱ.若二叉树非空，1.访问根结点;2.前序遍历左子树;3.前序遍历右子树

void PreOrderTraverse(BiTree T) {
    if (T == NULL)  return OK;  //空二叉树
    else {
        visit(T);   //访问根节点
        PreOrderTraverse(T->lchild);    //递归遍历左子树
        PreOrderTraverse(T->rchild);    //递归遍历右子树
    }
}

遍历算法的实现——中序遍历

Ⅰ.若二叉树为空，则空操作; Ⅱ.否则：1.中序遍历左子树;2.访问根结点;3.中序遍历右子树

void InOrderTraverse(BiTree T) {
    if (T == NULL)  return OK;  //空二叉树
    else {
        InOrderTraverse(T->lchild); //递归遍历左子树
        visit(T);   //访问根结点
        InOrderTraverse(T->rchild); //递归遍历右子树
    }
}

遍历算法的实现——后序遍历

Ⅰ.若二叉树为空，则空操作： Ⅱ.否则 1.后序遍历左子树;2.后序遍历右子树;3.访问根结点;

void PostOrderTraverse(BiTree T) {
    if (T == NULL)  return OK;  //空二叉树
    else {
        PostOrderTraverse(T->lchild);   //递归遍历左子树
        PostOrderTraverse(T->rchild);   //递归遍历右子树
        visit(T);   //访问根结点
    }
}

时间复杂度均为O(n) 每个结点只访问一次 空间复杂度均为O(n) 栈占用的最大辅助空间

中序遍历非递归算法

二叉树中序遍历的非递归算法的关键: 在中序遍历过某结点的整个左子树后，如何找到该结点的根以及右子树。

基本思想:

(1) 建立一个栈 (2)根结点进栈，遍历左子树 (3)根结点出栈，输出根结点，遍历右子树。

参考王卓老师p50,算法5.2：https://www.bilibili.com/video/BV1nJ411V7bd?p=90

栈的存储结构的建立

typedef struct{
    int *base;  //栈底指针
    int *top;   //栈顶指针
    int stacksize;  //栈可用最大容量
}SqStack;
SqStack S;

顺序栈的初始化操作：构造一个空栈

int InitStack(SqStack &S){  //构造一个空栈
    S.base=new int[MAXSIZE];    //或S.base=(int*)malloc(MAXSIZE*sizeof(int));
    if(!S.base) exit(FALSE); //存储分配失败
    S.top=S.base;   //栈顶指针等于栈底指针
    S.stacksize=MAXSIZE;
    return OK;
}

判断顺序栈是否为空

int StackEmpty(SqStack S){  //若栈为空，返回TURE,否则返回FALSE
    if(S.top==S.base)
        return TRUE;
    else
        return FALSE;
}

顺序栈的入栈

int Push(SqStack &S,int e){
    if(S.top-S.base==S.stacksize) return ERROR; //栈满
    *S.top++=e; //*S.top=e; S.top++;
    return OK;
}

顺序栈的出栈

int Pop(SqStack &S,int &e){     //出栈操作：删除S的站点元素An,并用e返回其值
    if(S.top==S.base) return ERROR; //若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK;否则返回ERROR
    e=*--S.top;     //--S.top; e=*S.top;
    return OK;
}

算法实现

int InOrderTraverse_no(BiTree T) {
    BiTree p, q;
    InitStack(S);
    p = T;
    while (p || !StackEmpty(S)) {
        if (p) {
            Push(S, p->data);
            p = p->lchild;
        } else {
            Pop(S, q->data);
            printf("%c", q->data);
            p = q->rchild;
        }
    }
    return OK;
}

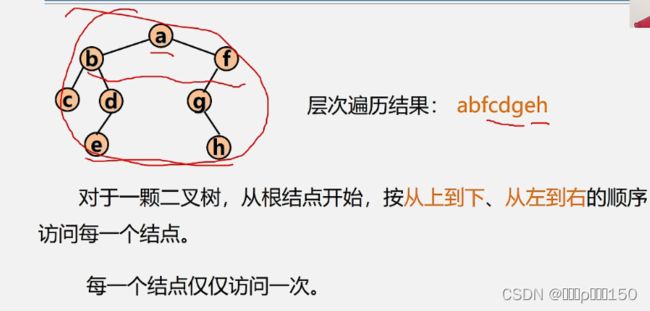
二叉树的层次遍历算法

Ⅰ.对于一颗二叉树，从根结点开始，按从上到下、从左到右的顺序访问每一个结点。 Ⅱ.每一个结点仅仅访问一次。

算法设计思路：使用一个队列 1.将根结点进队; 2.队不空时循环:从队列中出列一个结点*p，访问它; 若它有左孩子结点，将左孩子结点进队; 若它有右孩子结点，将右孩子结点进队。

参考王卓老师p91，https://www.bilibili.com/video/BV1nJ411V7bd?p=91

 使用队列类型定义

typedef struct Node {    // 定义二叉链
    char         data;   // 数据元素
    struct Node* lchild; // 指向左孩子节点
    struct Node* rchild; // 指向右孩子节点
} BTNode;                // struct Node 的别名
​
typedef struct Quene {      // 定义顺序队
    int     front;          // 队头指针
    int     rear;           // 队尾指针
    BTNode* data[MAXSIZE]; // 存放队中元素
} SqQueue;                  // struct Queue 的别名

初始化队列

void initQueue(SqQueue** q) {
    if (!((*q) = (SqQueue*)malloc(sizeof(SqQueue)))) {
        printf("内存分配失败！");
        exit(ERROR);
    }
    (*q)->front = (*q)->rear = -1; // 置 -1
}

判断队列是否为空

bool emptyQueue(SqQueue* q) {
    // 首指针和尾指针相等，说明为空。空-返回真，不空-返回假
    if (q->front == q->rear) {
        return true;
    }
    return false;
}

进队列

bool enQueue(SqQueue* q, BTNode* node) {
    // 判断队列是否满了。满（插入失败）-返回假，不满（插入成功）-返回真
    if (q->rear == MAXSIZE - 1) {
        return false;
    }
    q->rear++;               // 头指针加 1
    q->data[q->rear] = node; // 传值
    return true;
}

出队列

bool deQueue(SqQueue* q, BTNode** node) {
    // 判断是否空了。空（取出失败）-返回假，不空（取出成功）-返回真
    if (q->front == q->rear) {
        return false;
    }
    q->front++;                // 尾指针加 1
    *node = q->data[q->front]; // 取值
    return true;
}

算法实现

void levelOrder(BTNode* BT) {
    SqQueue* q;       // 定义队列
    initQueue(&q);    // 初始化队列
    if (BT != NULL) { // 根节点指针进队列
        enQueue(q, BT);
    }
    // 一层一层的把节点存入队列，当没有孩子节点时就不再循环
    while (!emptyQueue(q)) {      // 队不为空循环
        deQueue(q, &BT);          // 出队时的节点
        printf("%c", BT->data);   // 输出节点存储的值
        if (BT->lchild != NULL) { // 有左孩子时将该节点进队列
            enQueue(q, BT->lchild);
        }
        if (BT->rchild != NULL) { // 有右孩子时将该节点进队列
            enQueue(q, BT->rchild);
        }
    }
}

二叉树的建立

按先序遍历序列建立二叉树的二叉链表

参考王卓老师p92,https://www.bilibili.com/video/BV1nJ411V7bd?p=92

例：已知先序序列为：ABCDEGF (1)从键盘输入二叉树的结点信息，建立二叉树的存储结构; (2)在建立二叉树的过程中按照二叉树先序方式建立;

int CreateBiTree(BiTree &T){
    char ch;
    scanf("%c",&ch);
    if(ch=='#') T=NULL;
    else{
        if(!(T=(BiNode*)malloc(sizeof(BiNode))))    exit(OVERFLOW);
        T->data=ch; //生成根结点
        CreateBiTree(T->lchild);    //构造左子树
        CreateBiTree(T->rchild);    //构造右子树
    }
    return OK;
}

遍历算法的应用

参考王卓老师p93,http://(https://www.bilibili.com/video/BV1nJ411V7bd?p=93&spm_id_from=pageDriver

复制二叉树

如果是空树，递归结束; 否则，申请新结点空间，复制根结点; 递归复制左子树; 递归复制右子树;

int Copy(BiTree T, BiTree &NewT) {
    if (T == NULL) {    //如果是空树返回0
        NewT = NULL;
        return 0;
    } else {
        NewT = new BiNode;
        NewT->data = T->data;
        Copy(T->lchild, NewT->lchild);
        Copy(T->rchild, NewT->lchild);
    }
}

计算二叉树的深度

如果是空树，则深度为0; 否则，递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1;

int Depth(BiTree T) {
    int m, n;
    if (T == NULL)  return 0;   //如果是空树，返回0
    else {
        m = Depth(T->lchild);
        n = Depth(T->rchild);
        if (m > n)  return (m + 1);
        else return (n + 1);
    }
}

计算二叉树的结点总数

如果是空树，则结点个数为0； 否则，结点个数为左子树的结点个数+右子树的结点个数+1;

int NodeCount(BiTree T) {
    if (T == NULL)  return 0;
    else return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
}

计算二叉树叶子结点数

如果是空树，则叶子结点个数为0; 否则，为左子树的叶子结点个数+右子树的叶子结点个数;

int LeafCount(BiTree T) {
    if (T == NULL)  return 0;   //如果是空树，返回0
    if (T->lchild == NULL && T->rchild == NULL) return 1; //如果是叶子结点返回1
    else return LeafCount(T->lchild) + LeafCount(T->rchild);
}

求所有结点的深度

求二叉树高度的算法在这里不适用

采用递归遍历所有节点的时候， 递归函数的调用层数其实就是该节点的深度。

int point_Depth(BiTree T) {
      static int depth=0;
        depth++;
        if(!T){
            goto out;
        }else{
            printf("%c(%d)",T->data,depth);
            point_Depth(T->lchild);
            point_Depth(T->rchild);
        }
    out:
        depth--;
}

每当进入递归函数一次，depth就增加1，每退出函数一次，depth就减少1。

因为出函数代表回到上一根结点，层数减一，准备去另一子树；进函数代表去根结点的儿子结点，层数自然加一。

这里运用了static关键字，可以让变量变为静态全局变量,参考C++中的static - 知乎 (zhihu.com)，一般用于进入递归函数

完整代码实现（zjnu 数据结构 OJ 1007）

测试样例：ABD##E##C##

测试结果：A(1)B(2)D(3)E(3)C(2)

#include
using namespace std;
​
#define MAXSIZE 100
#define MAXTSIZE 100
#define TRUE 1
#define FALSE -1
#define OK 0
#define ERROR -2
​
typedef struct BiNode {
    int data;
    int deep=1;
    struct BiNode *lchild, *rchild; //左右孩子指针
} BiNode, *BiTree;
​
BiTree T;
​
​
int CreateBiTree(BiTree &T){
    char ch;
    scanf("%c",&ch);
    if(ch=='#') T=NULL;
    else{
        if(!(T=(BiNode*)malloc(sizeof(BiNode))))    exit(OVERFLOW);
        T->data=ch; //生成根结点
        CreateBiTree(T->lchild);    //构造左子树
        CreateBiTree(T->rchild);    //构造右子树
    }
    return OK;
}
​
int Depth(BiTree T) {
      static int depth=0;
        depth++;
        if(!T){
            goto out;
        }else{
            printf("%c(%d)",T->data,depth);
            Depth(T->lchild);
            Depth(T->rchild);
        }
    out:
        depth--;
}
​
int main(){
    CreateBiTree(T);
    Depth(T);
    return 0;
}