求三个球面交点的高效解法

一、问题描述

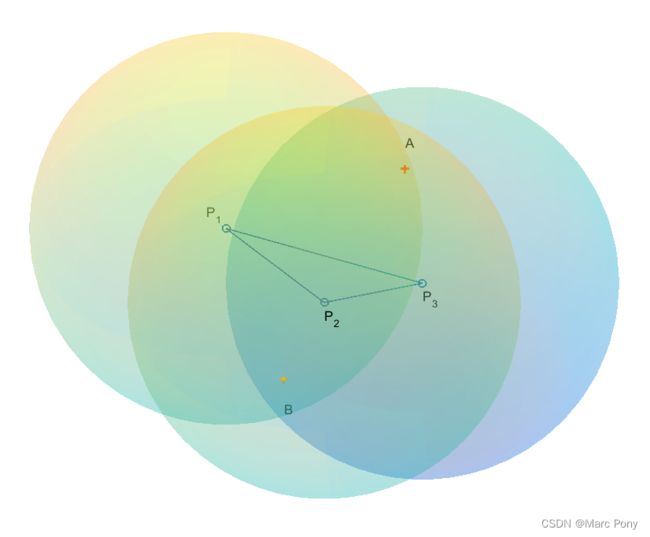
  如图，已知三个球面的球心坐标分别为$P_1(x_1,y_1,z_1),P_2(x_2,y_2,z_2),P_3(x_3,y_3,z_3)$。球半径分别为$r_1,r_2,r_3$，求三个球面的交点$A$和$B$的坐标。
  三个球面方程可以联立得到非线性方程组：
$$\{\begin{array}{llc}(x-x_1{)}^2+(y-y_1{)}^2+(z-z_1{)}^2=r_1^2& (1.1)& \\ (x-x_2{)}^2+(y-y_2{)}^2+(z-z_2{)}^2=r_2^2& (1.2)& \\ (x-x_3{)}^2+(y-y_3{)}^2+(z-z_3{)}^2=r_3^2& (1.3)& \end{array}\text{\hspace{1em}(1)}$$
  三球面交点的求解问题，一种很自然的想法是采用迭代法求解以上非线性方程组。然而非线性方程组的迭代求解方法存在以上问题：迭代初值选择不当，可能会导致迭代不收敛，并且迭代初值不容易确定；计算量较大；通过迭代的方法一次只能迭代计算一个解。
  读者可能会想到这样的方法：对于方程组(1)中的三个式子，两两作差刚好可以消去非线性方程组中的项$x^2,y^2,z^2$，得到三元一次方程组，将非线性方程组的求解问题转化为线性方程组的求解问题。线性方程组的求解问题存在唯一的全局最优解且求解算法简单，真是一个完美的解决方法？！但是，细想一下，发现不对劲：第一个球与第二个球相交为一个空间圆弧，空间圆弧与第三个球相交则(一般来说)有两个交点。那么问题出在哪里呢？这是由于，在对方程组(1)中的三个式子两两做差的过程中，关于待求变量$x,y,z$的平方项均被消去，约束条件变弱了。这个例子提醒了我，算法推导过程中切忌想当然！
  另外一种读者可能会想到的方法是：将式(1)的非线性方程组转化为无约束非线性优化模型：
$$\begin{gathered} min[(x-x_1{)}^2+(y-y_1{)}^2+(z-z_1{)}^2-r_1^2{]}^2 \\ +[(x-x_2{)}^2+(y-y_2{)}^2+(z-z_2{)}^2-r_2^2{]}^2 \\ +[(x-x_3{)}^2+(y-y_3{)}^2+(z-z_3{)}^2-r_3^2{]}^2\text{\hspace{1em}(2)} \end{gathered}$$
  求解无约束非线性优化模型与求解非线性方程组存在一样的问题。
  那么，有没有求三个球面交点的高效、有效、简洁的解法呢？本博文分别从代数法和几何法推导三个球面交点的高效解法。

二、推导步骤

代数法

  式(1.1)与式(1.3)相减，式(1.2)与式(1.3)相减，整理可得：
$$\{\begin{array}{ll}2(x_3-x_1)x+2(y_3-y_1)y+2(z_3-z_1)z=r_1^2-r_3^2-x_1^2+x_3^2-y_1^2+y_3^2-z_1^2+z_3^2& \\ 2(x_3-x_2)x+2(y_3-y_2)y+2(z_3-z_2)z=r_2^2-r_3^2-x_2^2+x_3^2-y_2^2+y_3^2-z_2^2+z_3^2& \end{array}\text{\hspace{1em}(3)}$$
  作变量代换，令
$$\{\begin{array}{ll}{a}_{11}=2(x_3-x_1)& \\ a_{12}=2(y_3-y_1)& \\ a_{13}=2(z_3-z_1)& \\ b_1=r_1^2-r_3^2-x_1^2+x_3^2-y_1^2+y_3^2-z_1^2+z_3^2& \\ a_{21}=2(x_3-x_2)& \\ a_{22}=2(y_3-y_2)& \\ a_{23}=2(z_3-z_2)& \\ b_2=r_2^2-r_3^2-x_2^2+x_3^2-y_2^2+y_3^2-z_2^2+z_3^2& \end{array}\text{\hspace{1em}(4)}$$
  式(3)写成：
$$\{\begin{array}{ll}{a}_{11}x+a_{12}y+a_{13}z=b_1& \\ a_{21}x+a_{22}y+a_{23}z=b_2& \end{array}\text{\hspace{1em}(5)}$$
  将式(5)看成关于未知数x和y的二元一次方程组，解得：
$$\{\begin{array}{ll}x=[(a_{22}{b}_1-a_{12}{b}_2)+(a_{12}{a}_{23}-a_{13}{a}_{22})z]/(a_{11}{a}_{22}-a_{12}{a}_{21})& \\ y=[(a_{11}{b}_2-a_{21}{b}_1)+(a_{13}{a}_{21}-a_{11}{a}_{23})z]/(a_{11}{a}_{22}-a_{12}{a}_{21})& \end{array}\text{\hspace{1em}(6)}$$
  作变量代换，令
$$\{\begin{array}{ll}{p}_1=(a_{12}{a}_{23}-a_{13}{a}_{22})/(a_{11}{a}_{22}-a_{12}{a}_{21})& \\ q_1=(a_{22}{b}_1-a_{12}{b}_2)/(a_{11}{a}_{22}-a_{12}{a}_{21})& \\ p_2=(a_{13}{a}_{21}-a_{11}{a}_{23})/(a_{11}{a}_{22}-a_{12}{a}_{21})& \\ q_2=(a_{11}{b}_2-a_{21}{b}_1)/(a_{11}{a}_{22}-a_{12}{a}_{21})& \end{array}\text{\hspace{1em}(7)}$$
  式(6)写成：
$$\{\begin{array}{ll}x=p_{1}z+q_1& \\ y=p_{2}z+q_2& \end{array}\text{\hspace{1em}(8)}$$
  将式(8)代入式(1.3)，展开并化简得到关于z的一元二次方程：
$$a{z}^2+bz+c=0\text{\hspace{1em}(9)}$$
  其中，
$$\{\begin{array}{ll}a=p_1^2+p_2^2+1& \\ b=2(p_1{q}_1-z_3+p_2{q}_2-p_1{x}_3-p_2{y}_3)& \\ c=q_1^2-2q_1{x}_3+q_2^2-2q_2{y}_3-r_3^2+x_3^2+y_3^2+z_3^2& \end{array}\text{\hspace{1em}(10)}$$
  求解式(9)的一元二次方程得到z，再将z代入式(8)得到x和y，至此求三个球面交点的代数解法推导完成。

几何法

  参考Andrew Wagner的python程序，自己推导三个球面交点的几何解法，推导过程如下：

  如上图，$A$为三个球面的一个交点，四面体$A{P}_1{P}_2{P}_3$的棱长均已知。$||A{P}_1||=r_1$，$||A{P}_2||=r_2$，$||A{P}_3||=r_3$，$||P_1{P}_2||$、$||P_2{P}_3||$和$||P_1{P}_3||$为球心的距离。
  以$P_1$为原点，向量$P_1{P}_2$为x方向，垂直于面$P_1{P}_2{P}_3$向上的法向量为z方向，y方向根据右手法则确定，建立局部坐标系$\{e_x-e_y-e_z\}$。
  过点$A$作线段$AC$垂直于面$P_1{P}_2{P}_3$交于$C$，过点$C$作$CD$垂直于$P_1{P}_2$交于点$D$，过点$P_3$作$P_{3}E$垂直于$P_1{P}_2$交于点$E$，连结$AD,C{P}_1,C{P}_3,CE,P_{3}E$。
  令$||P_{1}D||=x,||DC||=y,||CA||=z$，则点$A$的坐标可以写成：
$$A=P_1+x{e}_x+y{e}_y+z{e}_z\text{\hspace{1em}(11)}$$
  计算单位方向向量$e_x,e_y,e_z$及步长$x,y,z$则三球面的交点$A$便可计算。
  计算$e_x$:
  令$||P_1{P}_2||=d$
$$e_x=P_1{P}_2/||P_1{P}_2||=P_1{P}_2/d\text{\hspace{1em}(12)}$$
  计算$e_y$:
  令$||P_{1}E||=i$，容易得到：
$$e_y=E{P}_3/||E{P}_3||\text{\hspace{1em}(13)}$$
$$E{P}_3=P_1{P}_3-P_{1}E=P_1{P}_3-||P_{1}E||e_x=P_1{P}_3-i{e}_x\text{\hspace{1em}(14)}$$
  $i$为$P_1{P}_3$在$e_x$的投影，故有：
$$i=e_x\cdot P_1{P}_3\text{\hspace{1em}(15)}$$

  计算$e_z$:
$$e_z=e_x\times e_y\text{\hspace{1em}(16)}$$

  计算$x$:
  在三角形$A{P}_1{P}_2$中，根据余弦定理：
$$cos\angle A{P}_1{P}_2=(r_1^2+d^2-r_2^2)/(2r_{1}d)\text{\hspace{1em}(17)}$$
  由于线段$AC$垂直于面$P_1{P}_2{P}_3$，线段$P_1{P}_2$在面$P_1{P}_2{P}_3$内，因而线段$AC$垂直线段$P_1{P}_2$。由于线段$P_1{P}_2$垂直于线段$CD$，因而线段$P_1{P}_2$垂直于面$ACD$。由于线段$AD$在面$ACD$内，因而线段$P_1{P}_2$垂直于线段$AD$。在直角三角形$AD{P}_1$中，易得：
$$x=||P_{1}D||=||A{P}_1||cos\angle A{P}_1{P}_2=(r_1^2+d^2-r_2^2)/(2d)\text{\hspace{1em}(18)}$$
  计算$y$:
令$||P_2{P}_3||=j$，$j$为$P_1{P}_3$在$e_y$的投影，故有：
$$j=e_y\cdot P_1{P}_3\text{\hspace{1em}(19)}$$
  在三角形$CE{P}_3$中，由余弦定理，可得：
$$cos\angle DCE=cos\angle CE{P}_3=(||CE|{|}^2+j^2-||C{P}_3|{|}^2)/(2j||CE||)\text{\hspace{1em}(20)}$$
  根据勾股定理：
$$\{\begin{array}{ll}||CE|{|}^2=||AE|{|}^2-||AC|{|}^2& \\ ||C{P}_3|{|}^2=||A{P}_3|{|}^2-||AC|{|}^2& \end{array}\text{\hspace{1em}(21)}$$
  将式(21)代入式(20)得：
$$\begin{gathered} cos\angle DCE=cos\angle CE{P}_3=(||AE|{|}^2+j^2-r_3^2)/(2j||CE||) \\ =[(||AD|{|}^2+||DE|{|}^2)+j^2-r_3^2]/(2j||CE||) \\ =[r_1^2-x^2+(i-x{)}^2+j^2-r_3^2]/(2j||CE||) \\ =(r_1^2-r_3^2-2ix+i^2+j^2)/(2j||CE||)\text{\hspace{1em}(22)} \end{gathered}$$
  在直角三角形$CDE$中，
$$y=||DC||=||CE||cos\angle DCE=(r_1^2-r_3^2-2ix+i^2+j^2)/(2j)\text{\hspace{1em}(23)}$$
  计算$z$:
$$z=||CA||=\sqrt{||A{P}_1|{|}^2-||C{P}_1|{|}^2}=\sqrt{r_1^2-(x^2+y^2)}=\sqrt{r_1^2-x^2-y^2}\text{\hspace{1em}(24)}$$
  至此，三球面交点的几何解法推导完成。

三、MATLAB代码

function [A, B, sta] = calc_intersection_points_of_three_spheres2(P1, P2, P3, r1, r2, r3)
sta = 0;
A = [];
B = [];

x1 = P1(1);
y1 = P1(2);
z1 = P1(3);

x2 = P2(1);
y2 = P2(2);
z2 = P2(3);

x3 = P3(1);
y3 = P3(2);
z3 = P3(3);

a11 = 2 * (x3 - x1);
a12 = 2 * (y3 - y1);
a13 = 2 * (z3 - z1);
b1 = (r1 + r3) * (r1 - r3) + (x3 + x1) * (x3 - x1) + (y3 + y1) * (y3 - y1) + (z3 + z1) * (z3 - z1);

a21 = 2 * (x3 - x2);
a22 = 2 * (y3 - y2);
a23 = 2 * (z3 - z2);
b2 = (r2 + r3) * (r2 - r3) + (x3 + x2) * (x3 - x2) + (y3 + y2) * (y3 - y2) + (z3 + z2) * (z3 - z2);

temp = a11 * a22 - a12 * a21;
if abs(temp) < 1.0e-10
    sta = 1;
    return;
end

p1 = (a12 * a23 - a13 * a22) / temp;
q1 = (a22 * b1 - a12 * b2) / temp;
p2 = (a13 * a21 - a11 * a23) / temp;
q2 = (a11 * b2 - a21 * b1) / temp;

a = p1^2 + p2^2 + 1;
b = 2 * (p1 * q1 - z3 + p2 * q2 - p1 * x3 - p2 * y3);
c = q1^2 - 2 * q1 * x3 + q2^2 - 2 * q2 * y3 - r3^2 + x3^2 + y3^2 + z3^2;

delta = b^2 - 4 * a * c;
if delta < 0
    sta = 1;
    return;
end

z = [(-b + sqrt(delta)) / (2 * a); (-b - sqrt(delta)) / (2 * a)];
x = p1 * z + q1;
y = p2 * z + q2;
A = [x(1), y(1), z(1)];
B = [x(2), y(2), z(2)];

end

function [A, B, sta] = calc_intersection_points_of_three_spheres(P1, P2, P3, r1, r2, r3)
sta = 0;
A = [];
B = [];

%计算e_x
vectorP1P2 = P2 - P1;
d = norm(vectorP1P2);
if abs(d) < 1.0e-10
    sta = 1;
    return;
end
e_x = vectorP1P2 / d;

%计算e_y
vectorP1P3 = P3 - P1;
i = dot(e_x, vectorP1P3);
vectorEP3 = vectorP1P3 - i * e_x;
if norm(vectorEP3) < 1.0e-10
    sta = 1;
    return;
end
e_y = vectorEP3 / norm(vectorEP3);

%计算e_z
e_z = cross(e_x, e_y);

%计算x
x = (r1*r1 + d*d - r2*r2) / (2*d);

%计算y
j = dot(e_y, vectorP1P3);
if abs(j) < 1.0e-10
    sta = 1;
    return;
end
y = (r1*r1 - r3*r3 -2*i*x + i*i + j*j) / (2*j);

%计算z
temp = r1*r1 - x*x - y*y;
if temp < 0.0
    sta = 1;
    return;
end
z = sqrt(temp);

%计算交点坐标
A = P1 + x*e_x + y*e_y + z*e_z;
B = P1 + x*e_x + y*e_y - z*e_z;

end

clc
clear
close all

figure('color', 'w')
[xs,ys,zs] = sphere(50);
h = surf(xs + 0,ys + 0.5,zs + 1);
set(h, 'FaceAlpha', 0.2, 'LineWidth', 0.1)

hold on
h = surf(xs + 0.5,ys + 0,zs + 1);
set(h, 'FaceAlpha', 0.2, 'LineWidth', 0.1)

h = surf(xs + 1,ys + 1,zs + 0);
set(h, 'FaceAlpha', 0.2, 'LineWidth', 0.1)

axis equal tight
shading interp
axis off

P1 = [0 0.5 1];
P2 = [0.5 0 1];
P3 = [1 1 0];
r1 = 1;
r2 = 1;
r3 = 1;

[p_12_a, p_12_b, sta] = calc_intersection_points_of_three_spheres(P1, P2, P3, r1, r2, r3)
[p_12_A, p_12_B, sta] = calc_intersection_points_of_three_spheres2(P1, P2, P3, r1, r2, r3)

plot3([P1(1), P2(1), P3(1), P1(1)], [P1(2), P2(2), P3(2), P1(2)], [P1(3), P2(3), P3(3), P1(3)], '-o', 'linewidth', 1)
plot3(p_12_a(1), p_12_a(2), p_12_a(3), '+', 'linewidth', 2)
plot3(p_12_b(1), p_12_b(2), p_12_b(3), '+', 'linewidth', 2)
text(P1(1)-0.1, P1(2)+0.1, P1(3), 'P_1')
text(P2(1), P2(2)-0.1, P2(3), 'P_2')
text(P3(1), P3(2)-0.1, P3(3), 'P_3')
text(p_12_a(1), p_12_a(2), p_12_a(3)+0.2, 'A')
text(p_12_b(1), p_12_b(2)-0.2, p_12_b(3), 'B')

view(0,49)