数据结构实现之Splay伸展树
Splay Tree 是二叉查找树的一种,它与平衡二叉树、红黑树不同的是,Splay Tree从不强制地保持自身的平衡,每当查找到某个节点n的时候,在返回节点n的同时,Splay Tree会将节点n旋转到树根的位置,这样就使得SplayTree天生有着一种类似缓存的能力,因为每次被查找到的节点都会被搬到树根的位置,所以当80%的情况下我们需要查找的元素都是某个固定的节点,或者是一部分特定的节点时,那么在很多时候,查找的效率会是O(1)的效率!当然如果查找的节点是很均匀地分布在不同的地方时,Splay Tree的性能就会变得很差了,但Splay Tree的均摊时间复杂度还是O(logn)的。
摘自http://www.nocow.cn/index.php/Splay_Tree
PPT来自清华邓俊辉数据结构-BST-Splay(学堂在线有对应视频讲解)

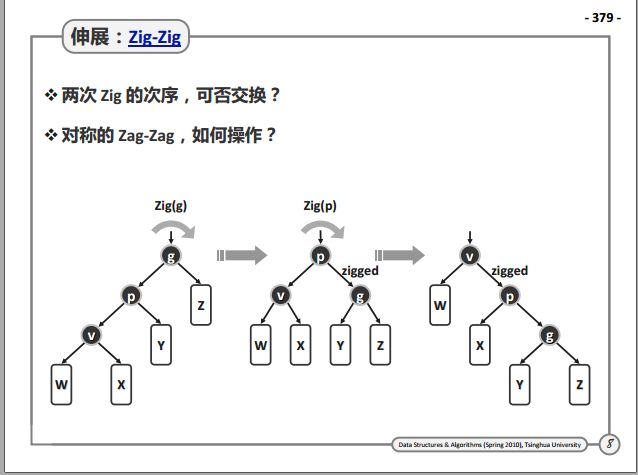
先zig(g)再zig(p)的要比先zig(p)再zig(g)的局部性效果要好,前者会使p成为g的左子结点,从而不能很好发挥SplayTree利用局部性的目的。

Splay Tree 结点定义
//Splay结点定义
private class Node {
public Node left;
public Node right;
public Node parent;
public Key key;
public Value val;
public Node(Key k,Value v) {
key = k; val = v; parent = null; left = null; right = null;
}
}splay
private Node splay(Node v) {
if(v == null) return null;
Node p,g;//v的父亲与祖父
//自下而上,反复对v做双层伸展
while((p=v.parent)!=null && (g = p.parent)!=null) {
Node gg = g.parent;//每轮之后v都以原曾祖父(great-grand parent)为父
if(isLChild(v)) {
if(isLChild(p)) {//zig-zig,zig(g)先g结点右旋,zig(p)再p右旋
attachAsLChild(g, p.right);
attachAsRChild(p,g);
attachAsLChild(p, v.right);
attachAsRChild(v,p);
}
else {//zig-zag,zig(p)先p右旋,再g左旋zag(g)
attachAsLChild(p,v.right);
attachAsRChild(v,p);
attachAsRChild(g,v.left);
attachAsLChild(v,g);
}
}
else {
if(isRChild(p)) {//zag-zag,zag(g)先g结点左旋,zip(p)再p左旋
attachAsRChild(g,p.left);
attachAsLChild(p,g);
attachAsRChild(p,v.left);
attachAsLChild(v,p);
}
else {//zag-zig,先p左旋,zag(p),再g右旋zig(g)
attachAsRChild(p,v.left);
attachAsLChild(v,p);
attachAsLChild(g,v.right);
attachAsRChild(v,g);
}
}
//若v原先的曾祖父gg不存在,则v现在应为树根
if(gg==null)v.parent = null;
else {//否则,gg此后应该以v作为左或右孩子
if(gg.left == g) attachAsLChild(gg,v);
else attachAsRChild(gg,v);
}
}//双层伸展结束时,必有g == NULL,但p可能非空
//若p果真非空,则额外再做一次单旋
if(p!=null && p == v.parent) {
if(isLChild(v)) {//zig
attachAsLChild(p,v.right);
attachAsRChild(v,p);
}
else {//zag
attachAsRChild(p,v.left);
attachAsLChild(v,p);
}
}
v.parent = null;
return v;
}查找
//查找
private Node find(Node p,Key key) {
if(p == null || key == null) return null;
Node prep = null;
while(p != null) {
prep = p;
int cmp = key.compareTo(p.key);
if(cmp<0) p = p.left;
else if(cmp>0) p = p.right;
else break;
}
root = splay(prep);
return root;
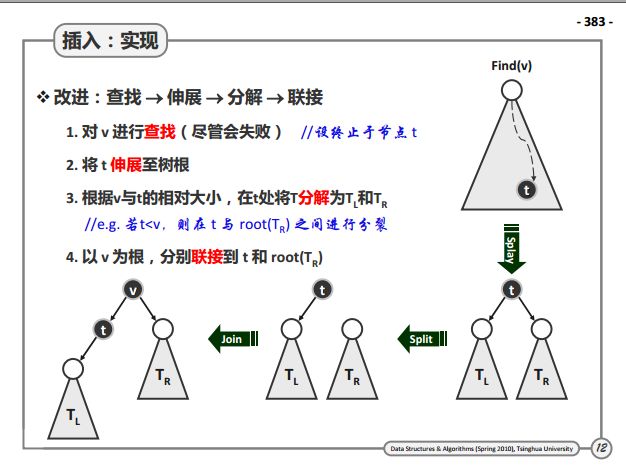
}插入
//插入
public void insert(Key key,Value val) {
if(key == null) return;
if(val == null) delete(key);
if(root == null) {
root = new Node(key,val);
return;
}
Node t = find(root,key);
int cmp = key.compareTo(t.key);
if(cmp == 0) {//更新value
root.val = val; return;
}
root = new Node(key,val);
//先把t分为两个左右子树,再合并
if(cmp<0) {//插入新根,以t->lChild和t为左、右孩子
Node x = t.left;
root.left = x;
root.right = t;
t.parent = root;
if(x != null) {
x.parent = root;
t.left = null;
}
}
else if(cmp>0) {//插入新根,以t和t->rChild为左、右孩子
Node x = t.right;
root.left = t;
root.right = x;
t.parent = root;
if(x != null) {
x.parent = root;
t.right = null;
}
}
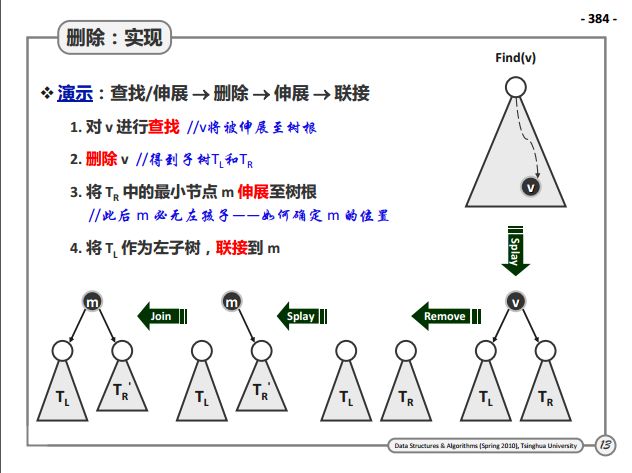
}删除
//删除
public void delete(Key key) {
if(key == null) return;
Node t = find(root,key);
if(t == null || key.compareTo(t.key) != 0)
return;
if(t.right == null) {//右子树为空
root = root.left; root.parent = null; return;
}
//右子树不空
//1.删除t结点,得到子树tl,tr
Node tl = t.left,tr = t.right;
tr.parent = null;
//2.将右子树最小结点min伸展至右子树树根,min一定没有左子结点
Node min = min(tr);
//3.将tl作为左子树链接到min上
min.left = tl;
if(tl != null) tl.parent = min;
root = min;
}完整代码
public class SplayTree ,Value>{
private Node root;
//Splay结点定义
private class Node {
public Node left;
public Node right;
public Node parent;
public Key key;
public Value val;
public Node(Key k,Value v) {
key = k; val = v; parent = null; left = null; right = null;
}
}
public SplayTree() {
root = null;
}
public Value find(Key key) {
root = find(root,key);
if(root == null || root.key.compareTo(key) != 0) return null;
return root.val;
}
//查找
private Node find(Node p,Key key) {
if(p == null || key == null) return null;
Node prep = null;
while(p != null) {
prep = p;
int cmp = key.compareTo(p.key);
if(cmp<0) p = p.left;
else if(cmp>0) p = p.right;
else break;
}
root = splay(prep);
return root;
}
//插入
public void insert(Key key,Value val) {
if(key == null) return;
if(val == null) delete(key);
if(root == null) {
root = new Node(key,val);
return;
}
Node t = find(root,key);
int cmp = key.compareTo(t.key);
if(cmp == 0) {//更新value
root.val = val; return;
}
root = new Node(key,val);
//先把t分为两个左右子树,再合并
if(cmp<0) {//插入新根,以t->lChild和t为左、右孩子
Node x = t.left;
root.left = x;
root.right = t;
t.parent = root;
if(x != null) {
x.parent = root;
t.left = null;
}
}
else if(cmp>0) {//插入新根,以t和t->rChild为左、右孩子
Node x = t.right;
root.left = t;
root.right = x;
t.parent = root;
if(x != null) {
x.parent = root;
t.right = null;
}
}
}
//删除
public void delete(Key key) {
if(key == null) return;
Node t = find(root,key);
if(t == null || key.compareTo(t.key) != 0)
return;
if(t.right == null) {//右子树为空
root = root.left; root.parent = null; return;
}
//右子树不空
//1.删除t结点,得到子树tl,tr
Node tl = t.left,tr = t.right;
tr.parent = null;
//2.将右子树最小结点min伸展至右子树树根,min一定没有左子结点
Node min = min(tr);
//3.将tl作为左子树链接到min上
min.left = tl;
if(tl != null) tl.parent = min;
root = min;
}
/***************************************************************************
* Splay tree helper functions.
***************************************************************************/
private Node splay(Node v) {
if(v == null) return null;
Node p,g;//v的父亲与祖父
//自下而上,反复对v做双层伸展
while((p=v.parent)!=null && (g = p.parent)!=null) {
Node gg = g.parent;//每轮之后v都以原曾祖父(great-grand parent)为父
if(isLChild(v)) {
if(isLChild(p)) {//zig-zig,zig(g)先g结点右旋,zig(p)再p右旋
attachAsLChild(g, p.right);
attachAsRChild(p,g);
attachAsLChild(p, v.right);
attachAsRChild(v,p);
}
else {//zig-zag,zig(p)先p右旋,再g左旋zag(g)
attachAsLChild(p,v.right);
attachAsRChild(v,p);
attachAsRChild(g,v.left);
attachAsLChild(v,g);
}
}
else {
if(isRChild(p)) {//zag-zag,zag(g)先g结点左旋,zip(p)再p左旋
attachAsRChild(g,p.left);
attachAsLChild(p,g);
attachAsRChild(p,v.left);
attachAsLChild(v,p);
}
else {//zag-zig,先p左旋,zag(p),再g右旋zig(g)
attachAsRChild(p,v.left);
attachAsLChild(v,p);
attachAsLChild(g,v.right);
attachAsRChild(v,g);
}
}
//若v原先的曾祖父gg不存在,则v现在应为树根
if(gg==null)v.parent = null;
else {//否则,gg此后应该以v作为左或右孩子
if(gg.left == g) attachAsLChild(gg,v);
else attachAsRChild(gg,v);
}
}//双层伸展结束时,必有g == NULL,但p可能非空
//若p果真非空,则额外再做一次单旋
if(p!=null && p == v.parent) {
if(isLChild(v)) {//zig
attachAsLChild(p,v.right);
attachAsRChild(v,p);
}
else {//zag
attachAsRChild(p,v.left);
attachAsLChild(v,p);
}
}
v.parent = null;
return v;
}
//判断结点n是否为父节点的左孩子
private boolean isLChild(Node n) {
Node p = n.parent;
return p.left == n;
}
//判断结点n是否为父节点的右孩子
private boolean isRChild(Node n) {
Node p = n.parent;
return p.right == n;
}
//在节点p与rc(可能为空)之间建立父(左)子关系
private void attachAsLChild(Node parent,Node lchild) {
parent.left = lchild;
if(lchild!=null)
lchild.parent = parent;
}
//在节点p与rc(可能为空)之间建立父(右)子关系
private void attachAsRChild(Node parent,Node rchild) {
parent.right = rchild;
if(rchild!=null)
rchild.parent = parent;
}
/***************************************************************************
* Utility functions.
***************************************************************************/
public Value min() {
if(root == null) return null;
root = min(root);
return root.val;
}
private Node min(Node x) {
if(x == null) return null;
while(x.left!=null)
x = x.left;
x = splay(x);
return x;
}
public Value max() {
if(root == null) return null;
root = max(root);
return root.val;
}
private Node max(Node x) {
if(x == null) return null;
while(x.right!=null)
x = x.right;
x = splay(x);
return x;
}
//中序遍历
public void preorder() {
System.out.println("preorder: ");
preorder(root);
System.out.println();
}
private void preorder(Node p) {
if(p == null) return;
System.out.print(p.key+" ");
preorder(p.left);
preorder(p.right);
}
//中序遍历
public void inorder() {
System.out.println("inorder: ");
inorder(root);
System.out.println();
}
private void inorder(Node p) {
if(p == null) return;
inorder(p.left);
System.out.print(p.key+" ");
inorder(p.right);
}
}