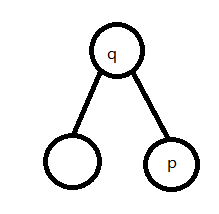
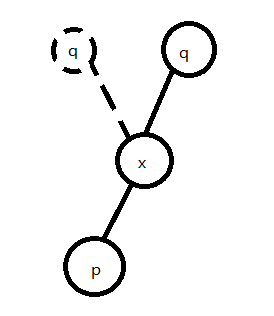
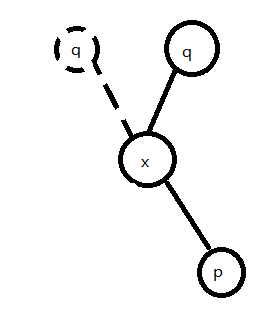
Splay（伸展树）的基本操作（c++）

$$\mathrm{M}\mathrm{y}\mathrm{f}\mathrm{i}\mathrm{r}\mathrm{s}\mathrm{t}\mathrm{b}\mathrm{l}\mathrm{o}\mathrm{g}$$

$$写给新手，大佬勿喷$$

---

目录

• 前置知识
• Splay是什么
• 支持的操作
  • 左旋
  • 右旋
  • 伸展
• 基本操作
  • 前驱
  • 后继
  • 插入
  • 删除
  • 查某数排名
  • 查排名为x的数
• 时间复杂度
• 例题
• 结语

---

前置知识

• 平衡树
• 二叉查找树
• 树上操作
• 指针
• 函数运用
• 基础数学知识

---

Splay是什么

Splay tree（伸展树）是一种 平衡树，由 Daniel Sleator 和 Robert Endre Tarjan 在1985年发明，用于保证 二叉查找树 的 尽量平衡¹ ，同时维护二叉查找树的性质²，使得查找操作的时间复杂度变低³。

Splay依赖于 伸展操作，而 伸展操作 依赖于 旋转⁴操作 。相对于其他平衡树，Splay代码较为简单，应用范围广，实用性较强，时间复杂度还行，不需要记录用于平衡树的冗余信息。

数据结构 Code：

struct Node
{
	long long val,size,sum;//节点的值、以此节点为根的子树的大小、相同值的个数
	Node *lson,*rson,*fa;//其左儿子、右儿子、父亲的指针
}tree[1000000];

基本维护 Code ：

Node *None,*root;//备用空节点和根节点
int kl=2;//数组大小
void shaobing()
{
	Node *p=tree+1,*q=tree+2;
	p->val=100000000;
	q->val=-100000000;
	p->size=2;
	q->size=1;
	p->sum=q->sum=1;
	p->lson=q;
	q->fa=p;
	root=p;
}//新建两个哨兵，防止越界
void Update(Node *p)
{
	if(p==None) return;//空就不用理他
	p->size=p->sum;
	if(p->lson!=None) p->size+=p->lson->size;
	if(p->rson!=None) p->size+=p->rson->size;
}//更新操作，当一个节点的位置改变了或新插入了一个节点时，需要重新维护size和same

---

支持的操作

1.左旋

字面意思，就是将某个节点旋到它父亲节点的父亲节点位置，同时维护BST性质。

举个例子：

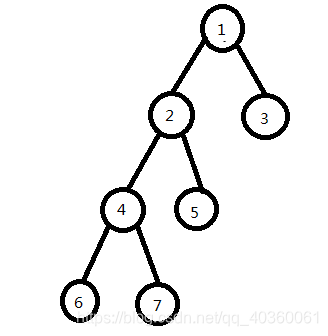
然后我们需要将 4 号节点左旋，也就是将 4 号节点旋到 2 号节点的父亲位置。

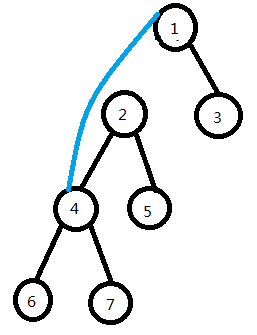
而 4 号节点不可能有三个儿子,所以我们将把 2 号节点下移，同时将 2 号节点的左儿子连至 2 号节点的右儿子 7 号节点， 4 号节点的右儿子连至 2 号节点，这样子就能维护 BST 性质。

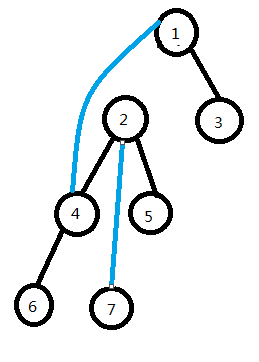
于是就变成了这样：

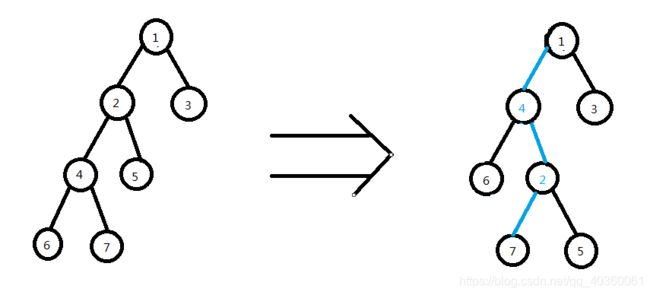
Code ：

void zig(Node *p)
{
	Node *Fa=p->fa;//指向它的父亲节点
	Fa->lson=p->rson;
	if(p->rson!=None) p->rson->fa=Fa;
	p->rson=Fa; 
	p->fa=Fa->fa;
	if(Fa->fa!=None) //需要特判，否则会出错
	{
		if(Fa->fa->lson==Fa)Fa->fa->lson=p;
		else Fa->fa->rson=p;
	}
	Fa->fa=p;
	Update(Fa);//先更新儿子节点，再更新父亲节点
	Update(p);
}

2.右旋

和左旋原理基本一样。上图（将 3 号节点旋至 5 号节点）：

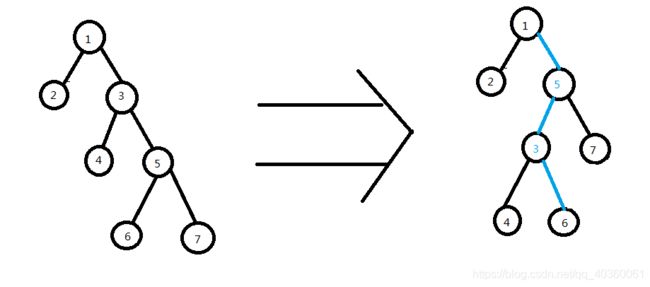
Code ：

void zag(Node *p)
{
	Node *Fa=p->fa;//指向它的父亲节点
	Fa->rson=p->lson;
	if(p->lson!=None) p->lson->fa=Fa;
	p->lson=Fa;
	p->fa=Fa->fa;
	if(Fa->fa!=None) //需要特判，否则会出错
	{
		if(Fa->fa->lson==Fa)Fa->fa->lson=p;
		else Fa->fa->rson=p;
	}
	Fa->fa=p;
	Update(Fa);//先更新儿子节点，再更新父亲节点
	Update(p);
}

3.伸展

伸展是Splay中最重要的操作，通俗的说， 它就是左旋和右旋外面套一层循环 ，通过指挥左旋和右旋来实现伸展，就好像人体通过扭动关节来伸懒腰。

伸展是将某一个节点通过旋转旋到另一个节点的儿子位置，如果是旋到根，那么我们就旋到 空节点的儿子位置 ，因为在树中，只有根没有父节点。

对于每一次的伸展，我们需要 分情况 ，设需要旋的节点为 p，要将 p 旋到其儿子位置的节点为 q：

• 当 p 已经是 q 的儿子时：

这是边界条件，直接退出循环

• 当 p 的父亲的父亲是 q 时：
  • p 是自己父亲的左儿子
    
    左旋 p，退出循环
  • p 是自己父亲的右儿子
    
    右旋 p ，退出循环
• 当 p 的父亲和爷爷都不是 q 时（我们设 p 的父亲是 y , p 的爷爷是 x ）
  • B 是 y 的左儿子， p 是 x 的左儿子
    
    左旋 B （一定要先旋 x ，否则无法保证时间复杂度为 $\mathrm{O}(n\log n)$ ），左旋 p
  • B 是 y 的右儿子， p 是 x 的右儿子
    
    右旋 B （一定要先旋 x ，否则无法保证时间复杂度为 $\mathrm{O}(n\log n)$ ），右旋 p
  • B 是 y 的左儿子， p 是 x 的右儿子
    
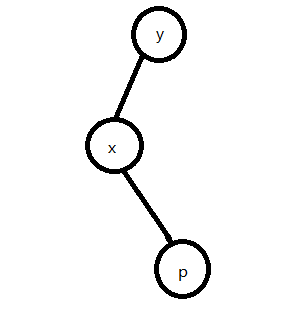
    右旋 p （这里只能旋 p ，自己思考一下为什么 ），左旋 p
  • B 是 y 的右儿子， p 是 x 的左儿子
    
    左旋 p （这里只能旋 p ，自己思考一下为什么），右旋 p

Code ：

void splay(Node *p,Node *Ft)
{
	while(p->fa!=Ft)
	{
		Node *q1=p->fa,*q2=q1->fa;
		if(q2==Ft)
		{
			if(q1->lson==p) zig(p);
			else zag(p);
			break;
		}
		bool Q1=(q1->lson==p),Q2=(q2->lson==q1)；
		//用bool函数记录，数值1代表左儿子状态，数值0代表右儿子状态。
		//Q1表示p的状态，Q2表示x的状态
		if(Q1&&Q2) zig(q1),zig(p);
		if((!Q1)&&(!Q2)) zag(q1),zag(p);
		if(Q1&&(!Q2)) zig(p),zag(p);
		if((!Q1)&&Q2) zag(p),zig(p);
	}
	if(p->fa==None) root=p;//这里一定要更新一下根
}

---

基本操作

1.前驱

前驱是基本操作中一个比较重要的操作，它支持着其它基本操作。

前驱的定义： 已知数x，在树中比x小且最大的数即为x的前驱。

递归一下，比x大就往左子树找，比x小就往右子树找，就能找到前驱。

因为我们定义了 哨兵 ，所以不用担心越界问题。

Code ：

Node *prev(int num,Node *now,Node *ans)//返回前驱的指针
{
	if(now==None) return ans;
	if(now->val<num) return prev(num,now->rson,now);//往右子树找
	return prev(num,now->lson,ans);//往左子树找
}

2.后继

后继也是基本操作中一个比较重要的操作，它支持着其它基本操作。

后继的定义： 已知数x，在树中比x小且最大的数即为x的前驱。

也是递归一下，比x小就往左子树找，比x大就往右子树找，就能找到后继。

一样不用担心越界问题。

Code ：

Node *succ(int num,Node *now,Node *ans)//返回后继的指针
{
	if(now==None) return ans;
	if(now->val>num) return succ(num,now->lson,now);//往右子树找
	return succ(num,now->rson,ans);//往左子树找
}

3.插入

我们要插入一个数 X ，一定要确定这个数在这棵树中的 具体位置 。那么如何确定呢？

我们可以将 X 的前驱旋到根，将 X 的后继旋到它前驱的右儿子位置。因为 一个数的前驱和后继只有一种 ，所以 X 的后继的左儿子为空或权值为 X 的节点。那么我们就可以插入 X 了。

Code ：

Node *Newnode(Node *p,int num)
{
	kl++;//数组大小
    Node *q=tree+kl;//获取数组地址
    q->fa=p;
    q->val=num;
    q->size=1;
    q->sum=1;
    return q;
}
void Insert(int num)
{
    Node *p=prev(num,root,None);
    splay(p,None);//伸展至根（不用判断是否为空，因为有哨兵）
    Node *q=succ(num,root,None);
    splay(q,p);//伸展至前驱右儿子
    if(q->lson!=None) q->lson->sum++,q->lson->size++;//相同只same++
    else q->lson=Newnode(q,num);//新建节点
    Update(q);
    Update(p);//更新
}

4.删除

原理和插入一样。

Code ：

void Delete(int num)
{
    Node *p=prev(num,root,None);
    splay(p,None);
    Node *q=succ(num,root,None);
    splay(q,p);
	if(q->lson->sum==1) q->lson=None;
	else q->lson->sum--;
	Update(q->lson);//如果有多个相同的数，要更新
    Update(q);
    Update(p);
}

5.查某数排名

已知某数 x ，求它在树中的排名。

同插入删除一样，直接用前驱后继找出排名，但要将找出的数旋至根，因为 时间复杂度需要这样维护⁵。

Code ：

int find(int num)
{
	Node *p=prev(num,root,None);
    splay(p,None);
    Node *q=succ(num,root,None);
    splay(q,p);
    splay(q->lson,None);//旋至根
    return root->lson->size;//原本是root->lson->size+1为它的排名，减去哨兵
}

6.查排名为x的数

既然是查排名为 x 的数，那么我们要先明白：对于任何一个节点，它的排名如何求。

首先，一个数的排名就等于 比它小的点的个数+1 ，这一点很容易推断，但可能有一些同学会认为，对于一个点，它的左子树肯定比它小，所以只要它左子树 size + 1就行了。

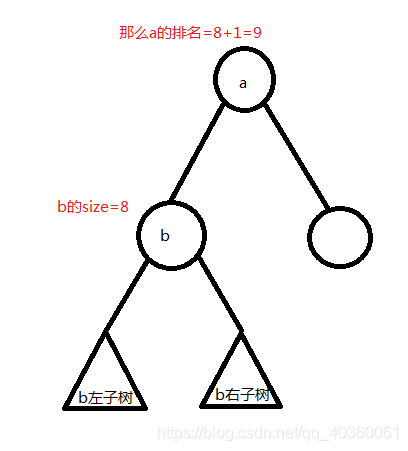
或

可是，这仅当 节点是根 或 节点是其父亲的左儿子 时才成立。事实上，情况有可能是这样的：

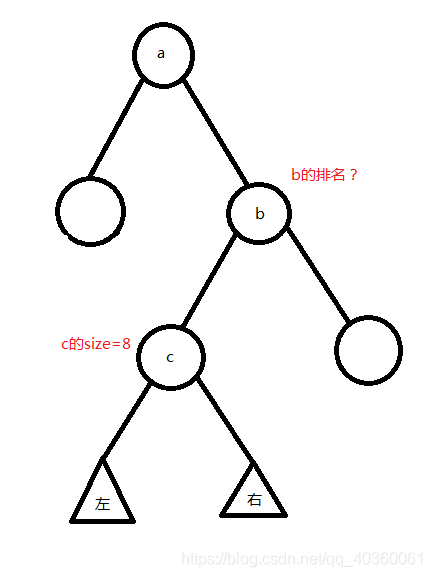
那么这时如何求呢？

我们知道， a 一定小于 b ，所以比 b 小的数有这么多：

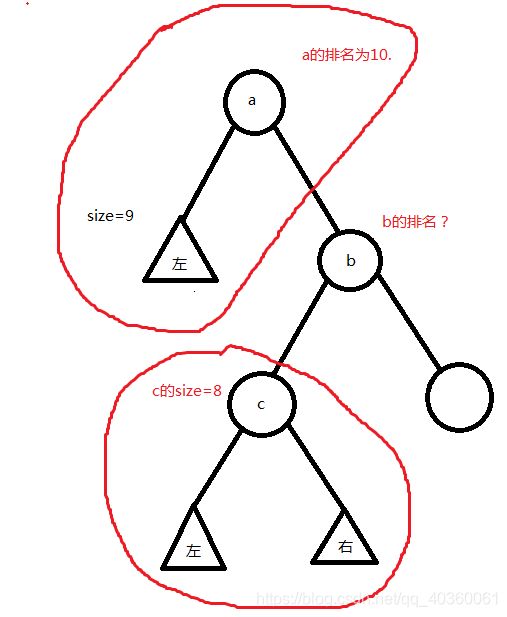
而我们事先求出了 a 的排名，那么 b 的排名就是 ：

a的排名+ a的相同数字的数量 - 1（自己想想为什么要减1） + c的size

当然你也可以这么算：

a的size - b的size + c的size

往后的节点以此类推。

Code ：

Node *ranking(int rank,Node *now,int nrank)
//nrank记录父亲节点的排名，传进来时是-1，因为定了哨兵
{
	int Rank=nrank+1;
	if(now->lson!=None) Rank+=now->lson->size;//特判一下，避免出错
	if(Rank<=rank && Rank+now->sum-1>=rank) return now;
	//因为同数值的数可能有多个，所以要判断排名x是否在这个范围
	if(Rank<rank) return ranking(rank,now->rson,Rank+now->sum-1);
	//往右子树找
	else return ranking(rank,now->lson,Rank-now->lson->size-1);
	//往左子树找
}

---

时间复杂度

任何一种平衡树的时间复杂度都与它的平衡度有关。总的来说，Splay是通过不断地随机旋转来维护平衡 ， 因为平衡的几率非常大 ， 所以我们可以认为Splay就是平衡的。也就是说 ，Splay的时间复杂度大约为 $\mathrm{O}(n\log n)$ 。

算出它的实际时间复杂度是一个很难的问题。很多同学知道Splay的时间复杂度是 $\mathrm{O}(n\log n)$ ，但不知道怎么求。遗憾的是，我就是其中之一。感兴趣的同学可以看看这位大佬的博客：

伸展树（Splay）复杂度证明

---

例题

P3369 【模板】普通平衡树

参考Code ：

//码风有些丑，请大佬见谅。
#include
using namespace std;
int n;
struct Node
{
	long long val,size,sum;
	Node *lson,*rson,*fa;
}tree[1000000];
Node *None,*root;
int kl=2;
void shaobing()
{
	Node *p=tree+1,*q=tree+2;
	p->val=100000000;
	q->val=-100000000;
	p->size=2;
	q->size=1;
	p->sum=q->sum=1;
	p->lson=q;
	q->fa=p;
	root=p;
}
void Update(Node *p)
{
	if(p==None) return;
	p->size=p->sum;
	if(p->lson!=None) p->size+=p->lson->size;
	if(p->rson!=None) p->size+=p->rson->size;
}
Node *Newnode(Node *p,int num)
{
	kl++;
    Node *q=tree+kl;
    q->fa=p;
    q->val=num;
    q->size=1;
    q->sum=1;
    return q;
}
void zig(Node *p)
{
	Node *Fa=p->fa;
	Fa->lson=p->rson;
	if(p->rson!=None) p->rson->fa=Fa;
	p->rson=Fa; 
	p->fa=Fa->fa;
	if(Fa->fa!=None) 
	{
		if(Fa->fa->lson==Fa)Fa->fa->lson=p;
		else Fa->fa->rson=p;
	}
	Fa->fa=p;
	Update(Fa);
	Update(p);
}
void zag(Node *p)
{
	Node *Fa=p->fa;
	Fa->rson=p->lson;
	if(p->lson!=None) p->lson->fa=Fa;
	p->lson=Fa;
	p->fa=Fa->fa;
	if(Fa->fa!=None) 
	{
		if(Fa->fa->lson==Fa)Fa->fa->lson=p;
		else Fa->fa->rson=p;
	}
	Fa->fa=p;
	Update(Fa);
	Update(p);
}
void splay(Node *p,Node *Ft)
{
	while(p->fa!=Ft)
	{
		Node *q1=p->fa,*q2=q1->fa;
		if(q2==Ft)
		{
			if(q1->lson==p) zig(p);
			else zag(p);
			break;
		}
		bool Q1=(q1->lson==p),Q2=(q2->lson==q1);
		if(Q1&&Q2) zig(q1),zig(p);
		if((!Q1)&&Q2) zag(p),zig(p);
		if(Q1&&(!Q2)) zig(p),zag(p);
		if((!Q1)&&(!Q2)) zag(q1),zag(p);
	}
	if(p->fa==None) root=p;
}
Node *prev(int num,Node *now,Node *ans)
{
	if(now==None) return ans;
	if(now->val<num) return prev(num,now->rson,now);	
	return prev(num,now->lson,ans);
}
Node *succ(int num,Node *now,Node *ans)
{
	if(now==None) return ans;
	if(now->val>num) return succ(num,now->lson,now);
	return succ(num,now->rson,ans);
}
void Insert(int num)
{
    Node *p=prev(num,root,None);
    if(p!=None) splay(p,None);
    Node *q=succ(num,root,None);
    splay(q,p);
    if(q->lson!=None) q->lson->sum++,q->lson->size++;
    else q->lson=Newnode(q,num);
    Update(q);
    Update(p);
}
void Delete(int num)
{
    Node *p=prev(num,root,None);
    if(p!=None) splay(p,None);
    Node *q=succ(num,root,None);
    splay(q,p);
	if(q->lson->sum==1) q->lson=None;
	else q->lson->sum--,q->lson->size--;
    Update(q);
    Update(p);
}
int find(int num)
{
	Node *p=prev(num,root,None);
    if(p!=None) splay(p,None);
    Node *q=succ(num,root,None);
    splay(q,p);
    splay(q->lson,None);
    return root->lson->size;
}
Node *ranking(int rank,Node *now,int nrank)
{
	int Rank=nrank+1;
	if(now->lson!=None) Rank+=now->lson->size;
	if(Rank<=rank && Rank+now->sum-1>=rank) return now;
	if(Rank<rank) return ranking(rank,now->rson,Rank+now->sum-1);
	return ranking(rank,now->lson,Rank-now->lson->size-1);
}
int main()
{
	cin>>n;
	shaobing();
	for(int i=1;i<=n;i++)
	{
		int x,tl;
		cin>>x>>tl;
		if(x==1) Insert(tl);
		if(x==2) Delete(tl);
		if(x==3) cout<<find(tl)<<endl;
		if(x==4)
		{
			Node *p=ranking(tl,root,-1);
			splay(p,None);
			cout<<p->val<<endl;
		}
		if(x==5)
		{
			Node *p=prev(tl,root,None);
			splay(p,None);//旋至根维护平衡度
			cout<<p->val<<endl;
		}
		if(x==6)
		{
			Node *p=succ(tl,root,None);
			splay(p,None);//旋至根维护平衡度
			cout<<p->val<<endl;
		}
	}
	return 0;
}
//圆润结束

---

结语

讲了那么多理论知识，讲一讲个人对Splay的看法。不得不说Spaly的实用性很强，能结合很多其他的数据结构一起使用，代码也比红黑树这些大佬算法简单，不过细节有点多。 fhq-treap 更适合新手打，因为它更为简单（这里插个友链：浅谈FHQ-Treap）。

---

完）
（如果有做的不好的地方，欢迎批评）

---

---

---

---

---

1. 平衡：即树中每个的左右子数的节点数相等，是为了应对树退化成链的方法。 ↩︎

2. 二叉查找树的性质：对于任何一个节点，若左子树不空，则它左子树上的每个节点的数值都比它小，若右子树不空，则它右字数上的每个节点的数值都比它大。即 BST 性质。 ↩︎

3. 见后章：时间复杂度 ↩︎

4. 见支持的操作中的左旋和右旋。 ↩︎

5. 详见时间复杂度章 ↩︎