第1周学习：深度学习和pytorch基础

配套教材：北京交通大学《专知-深度学习》

01-绪论

人工智能，机器学习，深度学习之间的关系理解：人工智能是个目标，我们希望机器能像人去感知与思考；机器学习是实现该目标的一类方法；深度学习是实现该方法的一个点。

一、机器学习简介

适用于问题规模大，准则复杂度高，从数据中自动提取知识、语义或模式。机器学习的信息处理效率高，可以减少人工规则的主观性，具有较高的可信度，其设计过程如下：

1. 模型 ，针对问题建模（确定是线性回归问题还是其他）；
2. 策略 ，确定目标函数（比如采用欧氏距离作为准则还是其他）；
3. 算法，求解模型参数（根据目标函数求解最优模型的具体计算方法）；

二、几种学习模型

根据数据标记分类：
监督vs无监督：区别在于学习的样本有没有标记。

1. 无监督学习从数据中学习模式，适用于描述数据（聚类）；
2. 监督学习从数据中学习类别的分界面，适用于预测（分类）；
3. 半监督学习：由于标记样本的成本较高，只有少量标记样本，通过数据分布与正负例，预测样本数据；
4. 强化学习：使用未标记的数据，根据奖励反馈机制 。

根据数据分布分类：

1. 参数模型，对数据分布有假设，用有固定数量参数的（比如斜率，截距）进行刻画，数据需求少，常见线性回归、感知机、K-means。
2. 非参数模型，不对数据分布进行假设，所有的统计特性来源于数据本身，对数据适应性强但容易过拟合，常见KNN、SVM、决策树。

根据建模对象分类：
判别模型在数据空间中绘制边界，而生成模型则模拟数据在整个空间中的分布。

1. 生成模型：对于输入的X,Y的联合分布P(X,Y)建模，然后再利用贝叶斯公式分类。
2. 判别模型：输入特征X，直接输出最可能的Y。
   GANs由二者结合，GAN 模型有两个部分——生成器和判别器。生成模型捕获数据分布，判别模型估计样本来自训练数据而不是生成模型的概率。

三、名词解释

回归：regression，想象这样一个场景，一堆看似无规律的数据在你的图像上肆无忌惮的乱走，我们要做的是找出其中的规律模型，把他们行走的趋势和轨迹“重新组合起来”。

超平面：n-1维的线性子空间，如果空间是3维的，那么它的超平面是二维平面，而如果空间是二维的，则其超平面是一维线。

最小二乘法：原理及代码实现

过拟合vs欠拟合：拟合==训练误差

1. 欠拟合：模型复杂度低，训练集上误差大，无法得到数据背后的规律；
   解决方法为提高模型复杂度，比如增加训练轮数或者拓展分支。
2. 过拟合：模型复杂度高，泛化能力差，无法忽略噪声；
   解决方法为降低模型复杂度，比如剪枝或者dropout。

---

02-神经网络基础

一、为什么说神经网络是黑盒的？

随着深度学习的应用拓展，要发展思考深度学习“不能”做什么，这为我们后续的学习提供导向。
通过可视化隐藏层得知每一层提取了哪些特征，但还是无法得知它为什么这么做以及众多参数的意义，解释性差。

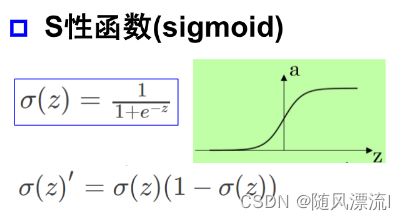
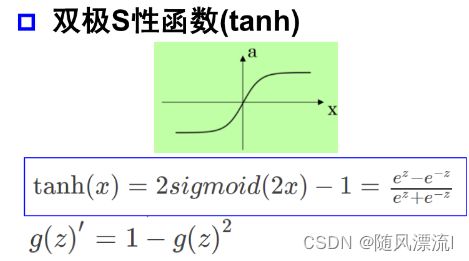
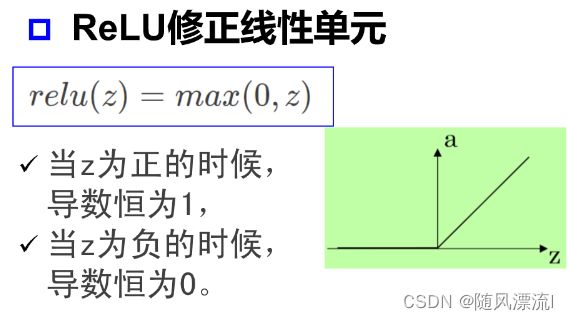
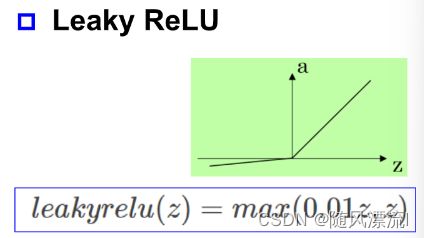
二、常用的激活函数

激活函数是用来加入非线性因素

1. sigmoid
   

2. tanh
   

3. ReLU
   

   用于解决误差反向传播引起的梯度消失以及饱和区问题；若跳出dead relu，则使用Leaky ReLU。

4. Leaky ReLU
   

三、万有逼近定理

单层感知器可用来实现“逻辑与、或、非”，且经过复合可变成多层感知器，比如加一个隐层就可实现非线性的同/异或问题。
如果一个隐层包含足够多的神经元，三层前馈神经网络（输入-隐层-输出）能以任意精度逼近任意预定的连续函数。
双隐层感知器逼近任意非连续函数：可解决任何复杂的分类问题。

四、层的作用

神经网络利用矩阵的线性变换加激活函数的非线性变换，将原始输入空间投影到线性可分的空间去分类。
神经网络测试
增加神经元节点数：增加线性转换能力，如升/降维，放大/缩小，旋转；
增加层数：增加激活函数的次数，即增加非线性转换能力，弯曲。

逐层预训练：自编码器，受限玻尔兹曼机，可以使网络具有较好的初始值，便于解决陷入局部极小值问题。

---

03-螺旋数据分类示例

一、SGD和ADAM

参数沿着负梯度方向更新可以使函数值下降，能迅速达到局部极小值点，通过优化算法对损失函数进行优化，以便寻找到最优的参数，使得损失函数的值最小。

1. 随机梯度下降（SGD）
   SGD算法是从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。
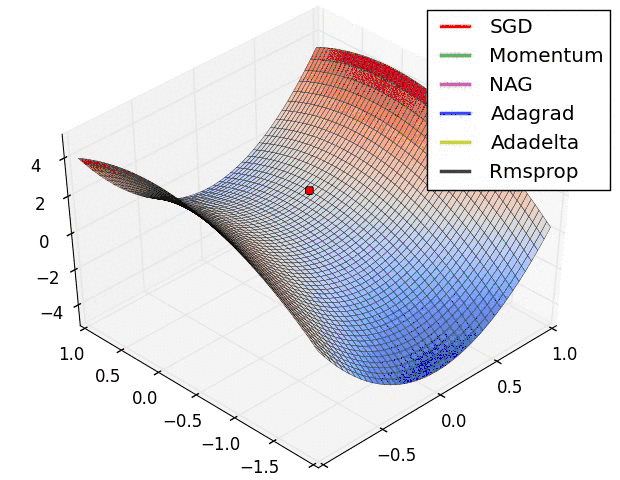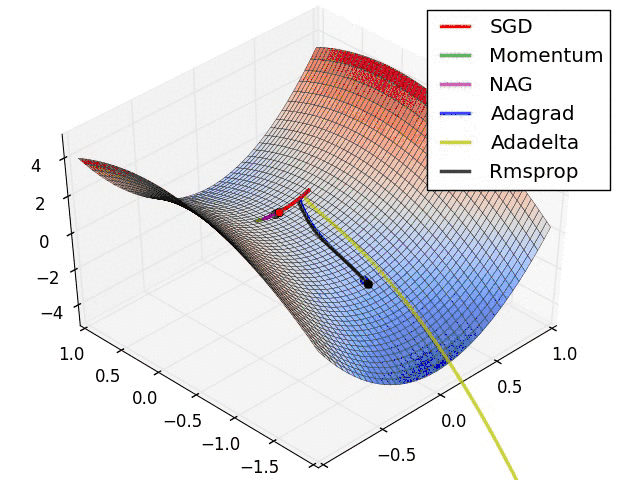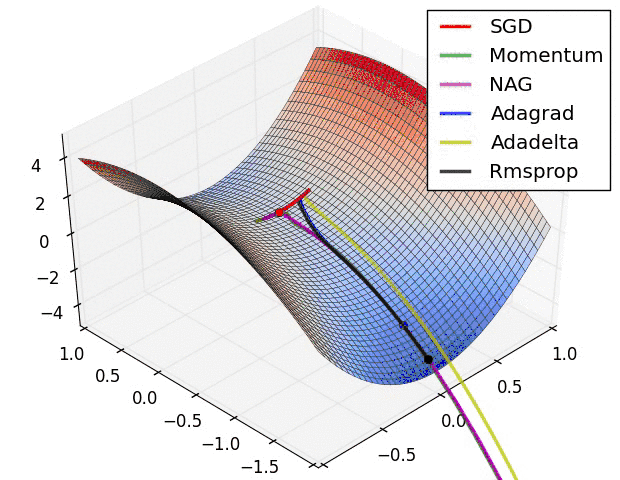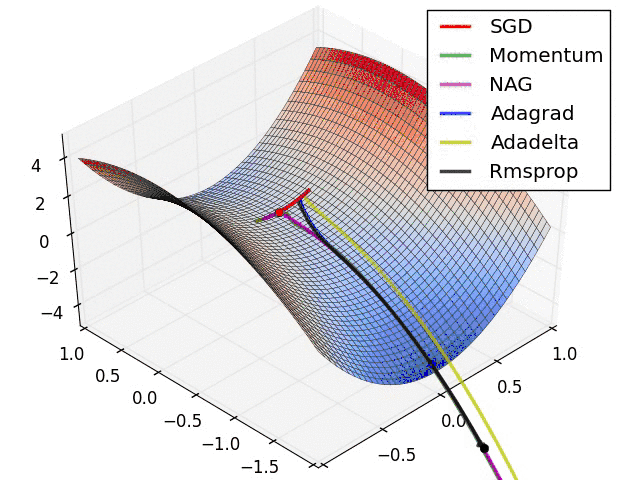
   但是SGD最大的缺点是下降速度慢，而且可能会在沟壑的两边持续震荡，停留在一个局部最优点，如下图所示。
2. 动量（Momentum）方法，惯性保持；Adagrad，环境感知，在应用中，我们希望更新频率低的参数可以拥有较大的更新步幅，而更新频率高的参数的步幅可以减小。AdaGrad方法采用“历史梯度平方和”来衡量不同参数的梯度的稀疏性，取值越小表明越稀疏；
3. Adam方法将惯性保持和环境感知这两个优点集于一身。

二、学习率的设定

学习率即为梯度下降的初始值，关于学习率的设定是有一些策略的，比如将初始学习率设置为一个较大的值，然后通过学习率衰减的策略来接近极值点。先使用较大的学习率快速收敛至极值点附近，再减小学习率使来回震荡的幅度减小，直至到达极值点，即为learning_rate，weight_decay参数的意义。

三、代码及结果

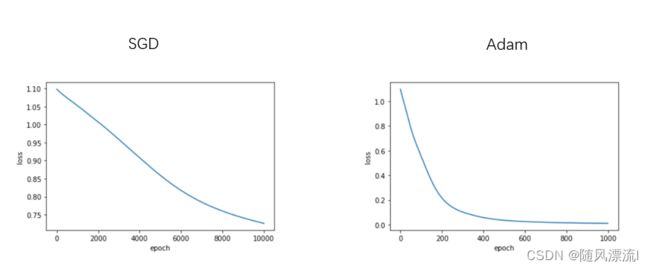
1. 从图中可得，在该分类场景下，SGD也可使结果收敛，只是需要的训练次数较多；而Adam优化算法，可在有限次数内迅速使loss函数收敛。
   
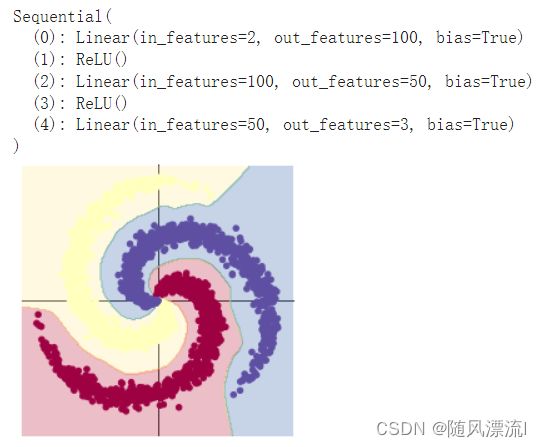
   通过增加神经网络的节点数和层数可以使其获得更好的效果，此时准确率可达0.999
   

2. 代码

!wget https://raw.githubusercontent.com/Atcold/pytorch-Deep-Learning/master/res/plot_lib.py
import random
import torch
from torch import nn,optim
#neural network,optim优化器
import math
import numpy as np
from IPython import display
#display图像显示
from plot_lib import plot_data,plot_model,set_default
import matplotlib.pyplot as plt

#在GPU上运行
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# device = torch.device("cuda:0")
print('device:',device)

seed = 12345 #相当于字典，在神经网络中，参数默认是进行随机初始化的。不同的初始化参数往往会导致不同的结果，当得到比较好的结果时我们通常希望这个结果是可以复现的，在pytorch中，通过设置随机数种子也可以达到这么目的。
random.seed(seed)
torch.manual_seed(seed)  # torch+CPU
torch.cuda.manual_seed(seed)  # torch+GPU

N = 1000  # 每类样本的数量
D = 2  # 每个样本的特征维度
C = 3  # 样本的类别
H = 100  # 神经网络里隐层单元的数量

X = torch.zeros(N * C, D).to(device)
Y = torch.zeros(N * C, dtype=torch.long).to(device)
for c in range(C):
  index = 0
  t = torch.linspace(0,1,N)
  inner_var = torch.linspace( (2*math.pi/C)*c, (2*math.pi/C)*(2+c), N) + torch.randn(N) * 0.2
  # 每个样本的(x,y)坐标都保存在 X 里
  # Y 里存储的是样本的类别，分别为 [0, 1, 2]
  for p in range(N * c,N * (c + 1)):
    X[p] = t[index] * torch.FloatTensor((math.sin(inner_var[index]), math.cos(inner_var[index])))
    Y[p] = c
    index += 1
print("Shapes:")
print("X:", X.size(),X.is_cuda)
print("Y:", Y.size())
# plot_data(X, Y)


learning_rate = 1e-3
lambda_l2 = 1e-5

# 模型分类
model = nn.Sequential(#一个有序的容器，神经网络模块将按照在传入构造器的 顺序 依次被添加到计算图中执行
    #这个函数是用来设置神经网络中的全连接层的，输入输出都是二维 tensor
    nn.Linear(D,H),               
    nn.ReLU(),
    nn.Linear(H,50),
    nn.ReLU(),
    nn.Linear(50,C)
)
model.to(device)

# 交叉熵损失函数
criterion = torch.nn.CrossEntropyLoss()
# 优化
optimizer = torch.optim.Adam(model.parameters(),lr=learning_rate,weight_decay=lambda_l2)

y = []
x = []
for t in range(1000):
  # 把数据输入模型，得到预测结果
  y_pred = model(X)
  # 计算损失和准确率
  loss = criterion(y_pred,Y)
  y.append(loss.item())
  x.append(t)
  score,predicted = torch.max(y_pred,1)# 最大的那个值存在 score 中，所在的位置（即第几列的最大）保存在 predicted 中
  acc = (Y == predicted).sum().float() / len(Y)
  print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
  display.clear_output(wait=True)

  # 反向传播前把梯度置0 grad在反向传播的过程中是累加的，也就是说上一次反向传播的结果会对下一次的反向传播的结果造成影响，则意味着每一次运行反向传播，梯度都会累加之前的梯度，所以一般在反向传播之前需要把梯度清零。
  optimizer.zero_grad()
  # 反向传播优化 
  loss.backward()
  # 更新全部参数
  optimizer.step()

  # print(y_pred.shape)
  # print(y_pred[10, :])
  # print(score[10])
  # print(predicted[10])


plot_model(X, Y, model)

# x=np.array(x)
# y=np.array(y)
# plt.plot(x,y)
# plt.xlabel("epoch")
# plt.ylabel("loss")
# plt.show()