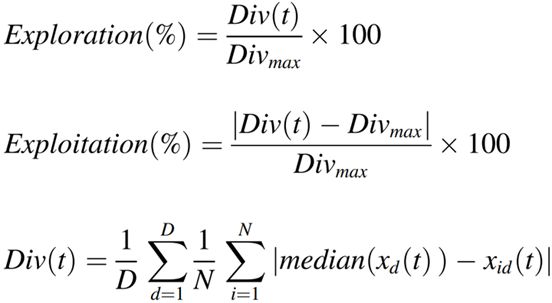优化算法改进的三个定性分析实验：收敛行为分析，种群多样性分析和探索开发分析

蛇优化算法是2022年提出的一种新的元启发式算法，发表在一区期刊Knowledge-Based Systems，该算法是一种模仿蛇特殊交配行为的新型智能优化算法。对于每条蛇（雄性/雌性），如果在食物数量足够，温度很低的条件下，就会努力得到最好的伴侣。

本期以蛇优化器Snake Optimizer (SO)为例，在23个基准测试函数上进行定性分析实验，这三个实验可以大大增加论文的说服力和提升文章质量，可以增加录用的概率，同时可以帮助研究者了解算法的特性，方便改进算法。下面我们将逐一介绍这三个实验。（可以参考文献：DMDE: Diversity-maintained multi-trial vector differential evolution algorithm for non-decomposition large-scale global optimization）。

​实验一：收敛行为分析（Convergence behavior analysis）

以单峰函数F1和多峰函数F23为例，SO求解不同测试函数的行为通过搜索历史、平均适应度值、轨迹、和收敛曲线4个指标进行评估。该实验由随机分布在二维搜索空间中的30个个体开始，在200次迭代中找到解。下图中第一列给出了测试函数的搜索空间。在第二列(搜索历史)中，用黑点说明了进化过程中个体的运动情况，并用红点表示全局最优解。这些观察结果证明了SO算法能够有效覆盖搜索空间，逼近问题的全局最优解。轨迹度量显示了代表性个体(第一个个体的第一个维度)在用于探索的初始迭代中的突然移动和用于利用搜索空间的最终迭代中的逐渐变化。在第三个度量中，第四列说明了种群的范围和均值，以显示搜索过程中种群的范围。最后，平均适应度显示了所有测试函数上的加速退化适应度值。这一行为表明SO算法能够在迭代一半之前找到有前景的解。

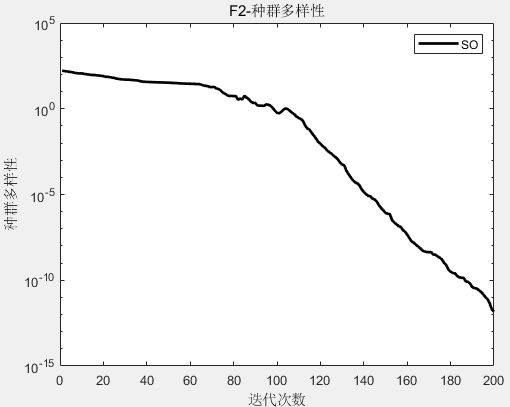
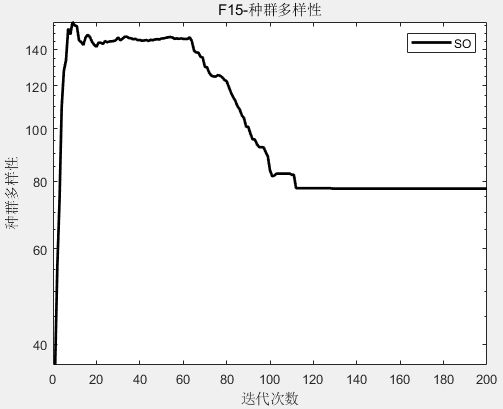
实验二：种群多样性分析 （Population diversity analysis）

计算公式如下。Ic表示每次迭代中总体与质量中心c的离散度，使用下面公式计算，其中参数xid表示迭代t时第i个个体的第d维的值。

​    实验结果如下图：以单峰函数F2和多峰函数F15为例，从单峰函数F1可以看出，种群多样性快速减少，表明算法有较好的开发能力，从多峰函数F23可以看出，种群多样性波动大，并且维持在较高水平，表明算法有较好的全局探索能力。

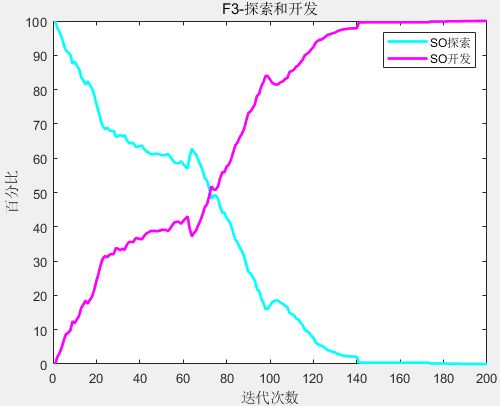
实验三：探索开发分析（Exploration and exploitation analysis）

公式如下：Divmax为整个迭代的最大多样性，参数xid表示迭代t时第i个个体的第d维的值。

得到的结果绘制在下图中，其中百分比(%)表示进化过程中所有种群的勘探和开发水平。以单峰函数F3和多峰函数F21为例，从单峰函数F3可以看出，开发的比例快速增加，表明算法有较好的开发能力，从多峰函数F21可以看出，探索的比例缓慢下降，表明算法有较好的全局探索能力。

下载后可获得以下内容：

主程序加上了详细中文注释，代码如下：

% 定性分析
clc; % 清空命令窗口
clear; % 清空工作空间
close all; % 关闭所有图形窗口

Function_name = 'F21'; % 选择测试函数的名称，可以是 F1 到 F23 中的任意一个
N = 30; % 搜索代理的数量
T = 200; % 最大迭代次数

% 载入所选基准函数的详细信息
[lb, ub, dim, fobj] = Get_Functions_details(Function_name);

% 运行SO算法，获取优化结果
[Xfood, fval, Convergence_curve, Trajectories, fitness_history, position_history, Exploration, Exploitation, Ic] = SO(N, T, lb, ub, dim, fobj);

% 创建一个图形窗口
figure('Position', [39 479 1740 267])

% 绘制搜索空间
subplot(1, 5, 1);
func_plot(Function_name);
title('参数空间')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
box on
axis tight

% 绘制搜索历史
subplot(1, 5, 2);
hold on
for k1 = 1:size(position_history, 1)
    for k2 = 1:size(position_history, 2)
        plot(position_history(k1, k2, 1), position_history(k1, k2, 2), 'o', 'markersize', 5, 'MarkerEdgeColor', 'k', 'markerfacecolor', '#1e90ff');
    end
end
plot(Xfood(1), Xfood(2), 'o', 'markersize', 10, 'MarkerEdgeColor', 'k', 'markerfacecolor', 'r', 'linewidth', 1);
title('搜索历史')
xlabel('x1')
ylabel('x2')
box on
axis tight

% 绘制测试函数曲面
subplot(1, 5, 2);
hold on
func_plot1(Function_name)

% 绘制轨迹
subplot(1, 5, 3);
hold on
semilogy(Trajectories(1, :), 'Color', 'g', 'linewidth', 2);
title('轨迹 ')
xlabel('迭代次数')
box on
legend('SO')
axis tight

% 绘制平均适应度
subplot(1, 5, 4);
hold on
a = mean(fitness_history);
semilogy(a, 'Color', 'b', 'linewidth', 2);
title('平均适应度 ')
xlabel('迭代次数')
box on
legend('SO')
axis tight

% 绘制收敛曲线
subplot(1, 5, 5);
semilogy(Convergence_curve, '-r', 'linewidth', 2);
title('收敛曲线')
xlabel('迭代次数');
ylabel('迄今为止获得的最佳分数');
box on
legend('SO')
axis tight

% 创建第二个图形窗口，绘制探索和开发的百分比
figure(2)
plot(Exploration, 'Color', 'c', 'LineWidth', 2)
hold on
plot(Exploitation, 'Color', 'm', 'LineWidth', 2)
xlabel('迭代次数')
ylabel('百分比')
title([Function_name,'-探索和开发'])
legend('SO探索', 'SO开发')

% 创建第三个图形窗口，绘制种群多样性
figure(3)
semilogy(Ic, 'Color', 'k', 'LineWidth', 2)
xlabel('迭代次数')
ylabel('种群多样性')
title([Function_name,'-种群多样性'])
legend('SO')