LeetCode 第十六天

104. 二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

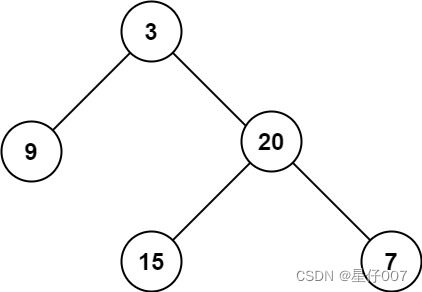
输入：root = [3,9,20,null,null,15,7]
输出：3
示例 2：

输入：root = [1,null,2]
输出：2

提示：

树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100

思路：递归方式采用后序遍历，先得到最下层的叶子结点的高度，然后对于每一个节点比较左右孩子的高度，取较大值+1得到本层节点的高度，然后返回给上一层。注意的是空节点一层高度为0。
层序遍历方式仅在基础的层序遍历基础上加上一个变量depth，每次遍历一层depth+1，遍历完毕得到树的高度。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        // 我靠，直接懵的 递归实现
            if(root == nullptr)
            return 0;
        int left = maxDepth(root->left);
        int right = maxDepth(root->right);
        return 1+max(left, right);
        // 层序遍历
        queue<TreeNode*> que;
        int depth = 0;
        if(root != nullptr)
            que.push(root);
        while(!que.empty())
        {
            int size = que.size();
            for(int i = 0; i < size; i++)
            {
                TreeNode* tmp = que.front();
                que.pop();
                if(tmp->left) que.push(tmp->left);
                if(tmp->right) que.push(tmp->right);
            }
            depth++;
        }
        return depth;
    }
};

559. N 叉树的最大深度
给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：3
示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

提示：

树的深度不会超过 1000 。
树的节点数目位于 [0, 104] 之间。

思路：同样是后序遍历，不过多叉树的递归和迭代都需要注意每一个分支节点的遍历。需要在遍历的时候加上一个for循环来完全遍历所有的孩子。总之这放在和二叉树的高度一起做是非常好的。

class Solution {
public:
    int maxDepth(Node* root) {
        // 递归法
        if(root == 0)
            return 0;
        int depth = 0;
        // n叉树有n个节点，因此需要一个for循环来遍历每个节点，还需要一个变量depth来记录该层节点的孩子高度最大值
        for(int i = 0; i < root->children.size(); i++)
        {
            depth = max(depth, maxDepth(root->children[i]));
        }
        return depth + 1;

        // 层序遍历迭代法
        queue<Node*> que;
        int depth = 0;
        if(root)
            que.push(root);
        while(!que.empty())
        {
            int size = que.size();
            for(int i = 0; i < size; i++)
            {
                Node* tmp = que.front();
                que.pop();
                // 层序遍历的主要改动点在这，即需要按照队头的孩子数确定遍历次数，然后依次将孩子加入队列。
                for(int j = 0; j < tmp->children.size(); j++)
                {
                    if(tmp->children[j]) que.push(tmp->children[j]);
                }
            }
            depth++;
        }
        return depth;
    }
};

111. 二叉树的最小深度
给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2
示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

思路：最小深度需要注意，必须是根节点到达叶子结点的路径长度，不能是到达空节点的长度，因此需要判断，如果是一个节点仅有一个孩子，那么不用返回两个孩子中的较小值，直接返回唯一孩子的深度；其余情况与最大深度类似。

class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == nullptr)
            return 0;
        int leftHeight = minDepth(root->left);
        int rightHeight = minDepth(root->right);
        // 最小深度中如果左右子树为空，返回零+1；仅一边空，返回另外一边深度+1；如果两边都不为空，返回较小一边深度+1。
        if(root->left == nullptr && root->right != nullptr)
        {
            return 1 + rightHeight;
        }
        if(root->right == nullptr && root->left != nullptr)
        {
            return 1 + leftHeight;
        }
        int result = 1 + min(leftHeight, rightHeight);
        return result;
    }
};

层序遍历法，直接搬运卡尔：

class Solution {
public:

    int minDepth(TreeNode* root) {
        if (root == NULL) return 0;
        int depth = 0;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++; // 记录最小深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
                if (!node->left && !node->right) { // 当左右孩子都为空的时候，说明是最低点的一层了，退出
                    return depth;
                }
            }
        }
        return depth;
    }
};

222. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

输入：root = [1,2,3,4,5,6]
输出：6
示例 2：

输入：root = []
输出：0
示例 3：

输入：root = [1]
输出：1

提示：

树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是 完全二叉树

进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

思路：本题最重要的解法是完全二叉树的自己特有解法，满足满二叉树的子树可以用公式直接计算。满二叉树也好判断，分别左子树一路到底，右子树一路到底，如果左右遍历的结点数相同，则直接公式计算，不用一步一步推。这个方法使得许多子树中间的结点都不用遍历，可以节省许多时间。

class Solution {
public:
// 普通二叉树的遍历方法
    int getNum(TreeNode* node)
    {
        if(node == nullptr)
            return 0;
        int leftNum = getNum(node->left);
        int rightNum = getNum(node->right);
        int treeNum = leftNum + rightNum + 1;
        return treeNum;
    }
    int countNodes(TreeNode* root) {
        // return getNum(root);

        // 完全二叉树的遍历方法
        if (root == nullptr)
            return 0;
            // 用于遍历的临时变量
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftNum = 0, rightNum = 0;
        // 左路一直走到黑
        while(left)
        {
            left = left->left;
            leftNum++;
        }
        // 右路一直走到黑
        while(right)
        {
            right = right->right;
            rightNum++;
        }
        // 左右高度相等，直接用公式计算
        if(leftNum == rightNum)
        {
            // 这里已经返回了，后面的不会再运行
            return (2 << leftNum) - 1;
        }
        // 如果不是满二叉树，直接一个一个遍历
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};