朴素贝叶斯原理分析及文本分类实战
朴素贝叶斯原理分析及文本分类实战
- 1.什么是贝叶斯
- 2.什么是朴素贝叶斯
- 3.如何用朴素贝叶斯来进行文本分类
-
- 问题1 数据精度问题
- 问题2 log(0)得到负无穷问题
- 4.程序设计
-
- 1 以单词为单位进行计数
- 2 以文本为单位进行计数
- 3 以变化的权重值进行计数
- 5 实验结果分析
- 6 总结
1.什么是贝叶斯
贝叶斯本质上就是条件概率分布,(通俗来讲,条件概率分布就是当我们知道了某一条件之后,所得出的用该条件所能推测得它属于的各个类别的概率)。
![]()
(1式)
w是我们的条件或者称为已知信息,c为对应的类别或者结果,那么(1)式所表达的含义就是由w推测得到c的概率大小。(我还是喜欢大白话,贝叶斯就像是破案一样,我们现在已经掌握了证据w,由证据w来推测嫌疑人是谁,我们目前有c1,c2,c3共3名嫌疑人,p(c1|w)表示c1为真凶的概率,p(c2|w)为c2是真凶的概率,p(c3|w)是c3为真凶的概率,p(c1|w)、p(c2|w)、p(c3|w)之和为1)
![]()
(2式)
将(1)式展开,可得到(2)式所示的结果。其中,p(w)表示条件w出现的概率,p(c,w)表示条件w和类别或结果c同时出现的概率。(我们可以这样来进行通俗理解,我们可以使用常见的分类任务来理解,比如给水果进行分类,c是水果的类别,w就是水果的特征,那么p(w)就是拥有特征w的水果在所有水果中的出现概率,p(c,w)是拥有特征w的c类水果在所有水果当中的出现概率。)p(w|c)为条件概率,已知c的情况下,对应的w出现的概率。P©表示c在所有数据中出现的概率。
2.什么是朴素贝叶斯
朴素贝叶斯是对贝叶斯的修正,目的是为了解决特征的稀疏性。(就以我们所熟知的分类任务为例子,我们的数据的特征向量是很难重复出现的,如果我们使用贝叶斯来制作分类器的话,p(w|c)我们得到的结果大概率是0,我们在训练模型的数据中很难找到与测试数据完全相同的特征向量。就比如文本分类,我们是将词语作为特征,一句文本中的所有词语组成一个特征向量,我们很难保证在分类器的训练数据当中有与测试数据完全相同组成的文本。)那么,朴素贝叶斯的做法如式(3)所示。
![]()
(3式)
朴素贝叶斯的做法是将一个由[w1,w2,w3…wn]这样一个特征向量转换为分离的特征。(这样做的好处就是我们在计算p(w|c)的时候,我们就可以在分类器的训练数据中找到对应存在的特征。我们可以认为是对特征的一次细化,让特征的颗粒度更小,更容易在分类器的训练数据中找到对应的特征。分母p(w)我们不需要去关心,它对于分类没有帮助,它是0.1还是1,对我分类的结果没有任何影响,所以朴素贝叶斯没有对它进行修正。)我们需要思考,用p(w1|c)p(w2|c)…p(wn|c)来代替p(w|c),会有什么影响呢?我们切断了特征之间的联系,但在一些情景当中特征之间的联系会很重要。对于文本分类而言,即使是使用贝叶斯模型,它也并未考虑到单词的顺序关系,只是考虑到了不同单词的数量之间的关联性。
3.如何用朴素贝叶斯来进行文本分类
我们将文本当中的单词作为特征,p(w)是单词w出现的概率(单词w出现的概率,如何计算呢?如果有一个文本数据当中,单词w出现了3次,我们应该计算单词出现1次还是3次呢?换句话讲,我们是应该以单词为单位进行计数还是以文本为单位进行计数呢?),p(w|c)是指单词w在c类别当中出现的概率,p©是指c类文本出现的概率(c类文本出现的概率,我们一定是通过以文本为单位的方式来进行统计,例如有10个文本,6个为正情感,4个为负情感,那么p(正)为0.4,p(负)为0.6)
问题1 数据精度问题
利用朴素贝叶斯模型,我们不是以文本整体为特征来统计出现概率,而是以单词为特征来统计特征出现的概率,让p(w|c)大部分情况是0的可能性大大降低。我们还需要考虑另外一个问题,因为我们最终是要在计算机上用编程语言设计出相应的程序,然而我们的数据是有一定的精度的。然而,在我们的朴素贝叶斯模型当中,当文本的单词很多的时候,分子中会有大量的p(wi|c)(i属于正整数)相乘,数据很可能非常小,当我们的数据结构无法表示这么小的数据的时候,我们得到结果就会变为0。这样的话,可能会给文本分类造成困扰,文本分类到各个类别的概率均为0时,我们无法确定文本到底是属于哪一个类别。
这时候,我们可以使用log函数来解决这个问题,我们可以将变量之间的相乘关系转换为相加减的关系,我们的数据就很难溢出了。当我们处理几百至几千单词的文本时,我们有信心保证模型不会出现数据溢出。我们可以再乘以一个系数进行缩放,这是一个让模型容纳更多单词的好办法。
![]()
(4式)
我相信你还是心存疑虑的,我们其实最关心的问题,其实是我们进行这种转换,是否会影响我们的分类结果?答案是肯定不会,因为y=log(x)(以e为底)是一个单调递增函数,这就意味着它保持了自变量的大小关系。(如果说p(c1|w)>p(c2|w)的话,那么一定有log(p(c1|w))>log(p(c2|w))成立,我们应用log函数,只是为了解决计算机编程语言表示数据时,精度不够的问题。)
问题2 log(0)得到负无穷问题
为了能够让贝叶斯应用到实际的分类任务,特别是文本分类任务,我们将使用朴素贝叶斯来代替贝叶斯,我们还用了log函数来解决精度问题(为什么一定要用log函数呢?一个很重要的特点是它能够让乘法变成加法,我们对朴素贝叶斯公式进行变形很简单,其它函数不具备这一特点。)。但是,当我们应用了log函数之后,有可能出现某一个单词在某个类别中没有出现过,即p(wi|c)=0,一旦出现这种情况,我们的朴素贝叶斯模型就会认为这一文本一定不是c类的,一点机会也不给,即使该文本其它单词都是更倾向于c类,也无济于事。(什么叫更倾向于c类呢?因为,我们的朴素贝叶斯模型是基于概率统计的模型,举个简单的例子,在文本情感分类任务当中,像hate、bad、poor在负面情绪中出现更多,当我们的文本有这些单词出现时,我们的文本就会更容易被分类成负面文本)但是,这是不公平的,而且,另外一个很重要的原因是我们的计算机编程语言也无法表示负无穷这样的数值。
这个时候,拉普拉斯正则化出现了。总的来说,它不会让p(wi|c)=0的情况出现,它会给p(wi|c)一个很小的概率值 ,保证它不为0,但同时还要保证概率总和为1。
我来举一个简单的例子,假设我们的朴素贝叶斯模型当中,我们一共统计到了3个单词,而在正向类别当中,3个单词的出现频次为如下表所示。
| 单词 | like | nice | ok |
|---|---|---|---|
| 正向类别 | 2 | 1 | 0 |
(表1:单词统计结果)
我们计算一下p(wi|c),分别为p(like|c)=2/3,p(nice|c)=1/3,p(ok|c)=0,(要是按照朴素贝叶斯的想法,一旦你的文本当中包含了ok这个单词,那么这个文本不可能会被分类为正向文本。这显然是不合情理的。)拉普拉斯的做法是为p(ok|c)一个小概率,同时保证p(like|c)、p(nice|c)、p(ok|c)的概率和为1。拉普拉斯正则化是按照式(5)来做的。
![]()
(5式)
在式(5)当中,n(wi,c)表示c类中单词wi的出现频次。我们来把拉普拉斯用到这个小案例当中吧,p(like|c)=3/6、p(nice|c)=2/6、p(ok|c)=1/6。P(ok|c)就不再为0啦,而且我们还保证了概率和 ∑ i p ( w i ∣ c ) \sum_{i} p(w_i|c) ∑ip(wi∣c)为1。(对于拉普拉斯正则化,我觉得很妙,但是我们还是可以活学活用,我们可以用比1更小的数值,如果你觉得让原本0概率的单词的概率增加得太大的话。)
![]()
(6式)
们可以把拉普拉斯公式写出如式(6)所示,我们可以再用表1的数据再进行一次计算,当a=0.1时,p(like|c)=0.6364、p(nice|c)=0.3333、p(ok|c)=0.0303。数据还是很直观的,我们将数据放在表2中对比一下。
| P(w|c)对比 | like | nice | ok |
|---|---|---|---|
| a=1 | 0.5 | 0.3333 | 0.1667 |
| a=0.1 | 0.6364 | 0.3333 | 0.0303 |
| a=0 | 0.6667 | 0.3333 | 0 |
(表2:拉普拉斯正则化效果对比)
我们选择的a值越小,概率p(wi|c)越接近于真实的情况。当然,你不可以选择太小的a值,因为防范p(wi|c)过小导致的下溢(计算机的编程语言无法表示这样小的数据,最经典的用法还是a=1的情况,我在程序设计部分,默认使用的就是a=1)。
至此,我们就已经完成了制作朴素贝叶斯文本分类模型的理论基础部分了。我们对贝叶斯进行了一系列的改造,目的就是为了能够让贝叶斯能够适应于我们的分类任务。
4.程序设计
这一个环节,我们要把朴素贝叶斯模型给落地了。我们先把思路梳理一下,我要做的模型一共有3种类型,分别是以单词为单位进行统计单词频次,以文本为单位统计单词频次,以变化的权重值来统计单词的频次。
我的目标是制作一个能够方便大家进行调用的工具模块,通过声明相应的对象,再调用相关的函数,便可以进行文本预测,十分方便。
我会着重为大家描述3种不同的朴素贝叶斯模型的不同之处。(其实,所谓的朴素贝叶斯模型,不过是把p(w|c)、p©、p(w)依据我们的训练数据求取出来,然后在预测的时候使用罢了。)
1 以单词为单位进行计数
我把程序给粘贴了出来,程序的设计流程遵循了我在理论部分所讲述的内容。程序的每一句代码,我都进行了注释,一是方便大家阅读,二是方便自己去温习。
if word not in self.word_list: # 检查单词是否不在在单词列表当中
self.word_list.append(word) # 将新的单词添加到单词列表当中
w_list = np.append(w_list, 1) # 该文本对应得单词记录表,也新添加一个位置
else: # 若单词在该文本当中
word_index = self.word_list.index(word) # 获取单词的序号
w_list[word_index] += 1 # 将相应的单词计数加1。
我挑选了该类型朴素贝叶斯模型的一段核心部分,我在计数单词频次时,是对文本当中的单词进行重复计数的。在文本当中,每遇到一个单词,我们就会给该单词的数量加1.
import numpy as np
import string
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
class Simple_Bayes_wordCount:
def __init__(self,data,labels,laplas=1):
"""
:param data:构建模型所使用的模型
:param labels: 数据对应的标签
"""
self.word_list = [] # 单词列表,不重复地记录训练数据种出现的单词,并使用下标代表相应的单词
self.c_list = [] # 类别列表,记录类别的标号,列表中的值为labels当中的标识,序号作为程序使用的类别标识
self.c_count = [] # 记录每一个类别的文本的数量
self.c_w = np.mat([]) # 矩阵,行号对应各个类别,列号对应各个单词(不重复)
stop_words = set(stopwords.words('english'))
for i in range(len(data)): # 对每一个文本进行遍历
str_lower = str.lower((data.iloc[i])) # 将第i个文本转换为小写
str_pure = str_lower.translate(str.maketrans('', '', string.punctuation))
# 去除没有具体词义的标点符号,我认为感叹号可以留下
word_tokens = word_tokenize(str_pure)
# word_tokens是一个列表对象
list_ = [w for w in word_tokens if not w in stop_words]
# 完成停用词的处理,
w_list = np.zeros(len(self.word_list))
# 建立该文本的单词列表,记录该文本中出现了哪些单词及其出现次数。1*|w|的数组,
# 第i个单元的值表示i所对应的单词的出现的次数
if labels.iloc[i] in self.c_list: # 判断当前的文本i的类别是否在c_list当中
c_idex = self.c_list.index(labels.iloc[i]) # 将文本当中的标号兑换成c_list
# 下标作为的类别标号。
self.c_count[c_idex] += 1
# 对应类别的文本的数目增加1,用于计算P(c),即某一类文本出现的概率。应当是基于
# 文本的数量进行统计,绝非对应类别单词的数量!!!
else: # 倘若列表当中还没有记录这一类别
c_idex = len(self.c_list) # c_idex是新类别的标号,c_list的数组下标
self.c_list.append(labels.iloc[i]) # 将新的标号添加到数组当中 self.c_count.append(1)
self.c_w = np.concatenate((self.c_w, np.mat(np.zeros(self.c_w.shape[1]))), axis=0)
# 由于检测到新的文本类别出现,我们在c_w矩阵当中需要增加一个新的行
for word in list_: # 对该文本当中的单词进行遍历
if word not in self.word_list: # 检查单词是否不在在单词列表当中
self.word_list.append(word) # 将新的单词添加到单词列表当中
w_list = np.append(w_list, 1) # 该文本对应得单词记录表,也新添加一个位置
else: # 若单词在该文本当中
word_index = self.word_list.index(word) # 获取单词的序号
w_list[word_index] += 1 # 将相应的单词计数加1,应该置为1就好了
# 对于单个文本,不应该对单词进行重复计数。
if len(w_list) > self.c_w.shape[1]: # 判断是否在该文本中出现了新的单词
self.c_w = np.concatenate((self.c_w, np.mat(np.zeros((self.c_w.shape[0], len(w_list) - self.c_w.shape[1])))), axis=-1)
# 对c_w矩阵,补加上新单词的位置
self.c_w[c_idex, :] = self.c_w[c_idex, :] + w_list
# 将该i号文本的记录,添加到c_w矩阵的对应行当中
print(i)
self.c_w = np.delete(self.c_w, self.c_w.shape[0] - 1, axis=0)
# 消除最后一行,这是我程序的缺陷之处,c_w有原始的一行,最后去除即可
c_num = np.sum(self.c_w,axis=-1)
#每个类别的单词总量
p_c_w = np.divide(self.c_w + laplas, np.array(c_num).reshape(-1, 1) + len(self.word_list)*laplas)
# 这个操作叫作拉普拉斯正则化,因为某些单词在一些类别当中根本没出现过,但是,按照
# 朴素贝叶斯的计算方式,有p(w1|c)*p(w2|c)...p(wn|c),若某一个单词w没在c类别当
# 中出现过的话,对应p(w|c)就是0.这是很不合理的事情,我们在文本分类这样的任务当中,
# 不能因为有一些在c当中没有统计到的单词,就完全扼杀了该文本属于该类别的可能。拉普拉斯
# 会使得每一个单词对应的p(w|c)都大于0,同时还保证了所有的p(w|c)相加,概率和仍为1.还
# 有,我们会把概率相乘换成对数相加的形式,因为当一个文本当中的单词过多,多个p(w|c)相乘
# 会得到一个非常小的数,计算机的浮点数据类型都无法准确表示,最终得到0.这显然给我们的
# 最后的比较造成很大的困扰,所以,拉普拉斯正则化十分重要。
p_c = np.divide(np.array(self.c_count), len(labels))
# 每个类别的文本的数量,处以总的文本的数量,获得p(c)即某一类别的文本出现的概率
w_num = np.sum(self.c_w, axis=0)
# 我们对c_w矩阵的每一行进行相加的操作,得到每一个类别统计到的单词数目。统计的方式很
# 考究,单个文本当中的单词,不应该进行重复统计,不同文本的相同单词要重复统计。我们既
# 防范了个别文本过度使用某词语所造成的破坏,也兼顾到了单词出现频率的计量。
p_w = np.divide(w_num, np.sum(w_num))
# 每个单词出现的次数除以总的单词出现次数,这里对单词数量的统计也很考究。我还是建议,单
# 个文本当中的单词,不要重复计量,或者压缩重复计量的比例,除了第一次计量之后,第二次就
# 累加0.1等操作,第三,第四......,我认为,这也是一种不错的方法,这些方法,我都会尝试
# 一下。我们这样操作,将过度使用某单词的影响进行了削减,也实际地考虑到了,过度使用和只
# 使用一次也是有区别的,就比如你在某个文本当中,写了一个like,说明你喜欢,是正面的。而
# 你写了5个like,实际上体现了你特别喜欢,喜欢的程度更深了,对于分类,应该有影响。也有一
# 些am is are, 我们最好不去统计这些单词,我们不重复计量,也是消除这些没有情感的单词的
# 影响,我们可以做一下统计,看这几种方式,是否让这些单词在不同类别之间分布得更加均匀。
# 了。P_w不影响最终的分类结果,因为对于w进行分类的时候,p(w)都是相同的。影响的是p_c
self.p_c_w_log = np.log(p_c_w)
self.p_c_log = np.log(p_c)
self.p_w_log = np.log(p_w)
# 我们把概率值,进行log运算,它不影响我们最终的比较结果,而且计算机能够准确地显示出log
# 函数的运算结果
def predict(self,data):
# 所谓的朴素贝叶斯文本分类器,不过是我们利用训练数据得到的一些变量而已。在分类的
# 时候,也只是使用这些变量,计算p(c1|w),p(c2|w),p(c3|w)...的值,值最大的对应
# 的ci,就是我们要分类的类别。
pwlog = self.p_w_log
word_list = self.word_list
pcwlog = self.p_c_w_log
pclog = self.p_c_log
c_list = self.c_list
sumplogw = np.sum(pwlog)
# 这个值就是log(p(w)),它对于分类结果,没有任何影响,但为了体现模型的完整性,我还是
# 把这一部分的内容给添加上了。
answers = []
# answers用于存放每个样本的分类结果
for i in range(len(data)): # 用于遍历所有的文本,i是文本的标号
str_lower = str.lower((data.iloc[i]))
# 将该文本处理为小写的,为什么要小写呢?因为,大写和小写,在情感的分类上是同等地位
# 我们没有必要再多花一份存储的开销,而且可能导致分类结果的波动,因为大写的单词,在
# 不同的类别的占比可能差异很大,所以把大写改成小写,好处真的很多。不仅仅是节省存储
# 空间,也让我们在对结果分类的时候,分类的结果更加合理,
str_pure = str_lower.translate(str.maketrans('', '', string.punctuation))
# 将文本的标点去除掉
list_ = str_pure.split()
# 以空格来将文本分割成数组
word_vector = np.zeros(len(word_list))
# 提取该文本的词向量,这里也很考究,是记录是否出现,还是记录出现的次数?还是以
# 0到1的权重来计入词向量。这里,我们也应该采用不同的方法来尝试一下。
for word in list_: # 对该文本对应的数组进行遍历
if word in word_list: # 判断文本当中的单词,是否在单词列表当中,只处理模型认识的单词
word_index = word_list.index(word)
# 获取单词在单词表当中的位置
word_vector[word_index] += 1
# 将相应的词向量的位置的值置为1,而不是加1.
word_vector = np.reshape(word_vector, (-1, 1))
# 将词向量的尺寸进行修改,将行向量修改为列向量,方便矩阵的乘法运算
pclog = np.reshape(pclog, (-1, 1))
# 将pclog从行向量修改为列向量
ans0 = (pcwlog * word_vector)
# c*w * w*1 = c*1,我们这样就完成了每个类别的的log(p(w|c))的运算
ans1 = ans0 + pclog
# 完成了log(p(w|c)*p(c))的计算
ans = ans1 - sumplogw
# 我还多此一举地把log(p(w))给捎带上了,它对于结果而言,可有可无,但是,我
# 不是搞工程,我是要分析这项简单技术的细节。
category_belongs = c_list[np.argmax(ans)]
# c*1的列向量,值最大的序号,对应于c_list的相应序号位置的值就是分类的结果
answers.append(category_belongs)
# 将分类的结果添加到answers当中进行记录
print(i)
# 给程序设计师,显示当前的文本位置。
return answers
2 以文本为单位进行计数
if word not in self.word_list: # 检查单词是否不在在单词列表当中
self.word_list.append(word) # 将新的单词添加到单词列表当中
w_list = np.append(w_list, 1) # 该文本对应得单词记录表,也新添加一个位置
else: # 若单词在该文本当中
word_index = self.word_list.index(word) # 获取单词的序号
w_list[word_index] = 1 # 将相应的单词计数加1,应该置为1就好了
# 对于单个文本,不应该对单词进行重复计数。
在这种方式当中,我不会对文本当中重复出现的单词进行反复计数了,而是一个文本当中,无论某个单词出现了多少次,我都只是为该单词的计数简单地赋值为1。事实上,我内心更倾向于这种方式,因为当某个特殊文本当中包含了大量了某种单词,将会破坏我们整体的计数平衡。(突然某个文本,土壤有100个单词high,原本high是一个情感不是那么分明的单词,结果一个文本用100个单词,一下子就把high变成有明显情感指向的单词。我们用一些久经沙场的数据集,是试不出来以单词为单位进行计数和以文本为单位进行计数的差别的,我们的朴素贝叶斯分类器是要为各式各样的文本服务的,正所谓林子大了,什么鸟都有,以文本为单位进行计数,具有更强的泛化能力。泛化能力就是指适应各种各样数据的能力。)
3 以变化的权重值进行计数
我把程序整个都贴了出来,因为变化的地方还是很多的。我在构造函数当中,添加了一个新的参数generate_weight,它是一个函数,我们可以利用这个函数来指定我们如何来计数单词的出现频次。
if word not in self.word_list: # 检查单词是否不在在单词列表当中
self.word_list.append(word) # 将新的单词添加到单词列表当中
w_list = np.append(w_list, 1) # 该文本对应得单词记录表,也新添加一个位置
wc_list = np.append(wc_list,1) #用于计数文本当中,单词出现次数的列表
else: # 若单词在该文本当中
word_index = self.word_list.index(word) # 获取单词的序号
wc_list[word_index] += 1
w_list[word_index] += generate_weight(wc_list,word_index) # 将相应的单词计数加上一定的权重
我们注意看,我采取的权重计数方式,也不是完全没有任何限制,我采取的是一种“出现越多越不值钱”的思想,权重值会采取某种方式由权重值1向0进行递减。权重计数的方式,实际上也考虑到了多次出现某个单词,它应该是会有更强一点的情感表达,我们也不能完全把在一个文本种重复出现的单词,完全抹杀掉。所以,我认为权重计数方式是更加合理的方式,我欢迎大家设计你认为合理的权重计数函数,看能否达到更好的分类效果。
class Simple_Bayes_wordweightCount:
def generate_wordweight(wordc_list,word_index):
if wordc_list[word_index]>1:
return 1
else:
return 0.1
def __init__(self,data,labels,laplas=1,generate_weight=generate_wordweight):
"""
:param data:构建模型所使用的模型
:param labels: 数据对应的标签
:param generate_weight:产生单词计数时的加权值,使用者需要自己
设计相应的函数,设计的规则是,第一个参数为记录当前各个单词出现的
次数的列表,第二个参数是单词序号,用于访问列表当中的单词,我也提供
了一个很简单的计算权重的默认函数。
"""
self.word_list = [] # 单词列表,不重复地记录训练数据种出现的单词
self.c_list = [] # 类别列表,记录类别的标号
self.c_count = [] # 记录每一个类别的文本的数量
self.c_w = np.mat([]) # 矩阵,行号对应各个类别,列号对应各个单词(不重复)
self.generate_weight =generate_weight
stop_words = set(stopwords.words('english'))
for i in range(len(data)): # 对每一个文本进行遍历
str_lower = str.lower((data.iloc[i])) # 将第i个文本转换为小写
str_pure = str_lower.translate(str.maketrans('', '', string.punctuation))
# 去除没有具体词义的标点符号,我认为感叹号可以留下
word_tokens = word_tokenize(str_pure)
# word_tokens是一个列表对象
list_ = [w for w in word_tokens if not w in stop_words]
# 完成停用词的处理,
w_list = np.zeros(len(self.word_list))
# 建立该文本的单词列表,记录该文本中出现了哪些单词及其出现次数。1*|w|的数组,
# 第i个单元的值表示i所对应的单词的权重结果
wc_list = np.zeros(len(self.word_list))
if labels.iloc[i] in self.c_list: # 判断当前的文本i的类别是否在c_list当中
c_idex = self.c_list.index(labels.iloc[i]) # 将文本当中的标号兑换成c_list
# 下标作为的类别标号。
self.c_count[c_idex] += 1
# 对应类别的文本的数目增加1,用于计算P(c),即某一类文本出现的概率。应当是基于
# 文本的数量进行统计,绝非对应类别单词的数量!!!
else: # 倘若列表当中还没有记录这一类别
c_idex = len(self.c_list) # c_idex是新类别的标号,c_list的数组下标
self.c_list.append(c_idex) # 将新的标号添加到数组当中
self.c_count.append(1)
self.c_w = np.concatenate((self.c_w, np.mat(np.zeros(self.c_w.shape[1]))), axis=0)
# 由于检测到新的文本类别出现,我们在c_w矩阵当中需要增加一个新的行
for word in list_: # 对该文本当中的单词进行遍历
if word not in self.word_list: # 检查单词是否不在在单词列表当中
self.word_list.append(word) # 将新的单词添加到单词列表当中
w_list = np.append(w_list, 1) # 该文本对应得单词记录表,也新添加一个位置
wc_list = np.append(wc_list,1) #用于计数文本当中,单词出现次数的列表
else: # 若单词在该文本当中
word_index = self.word_list.index(word) # 获取单词的序号
wc_list[word_index] += 1
w_list[word_index] += generate_weight(wc_list,word_index) # 将相应的单词计数加1,应该置为1就好了
# 对于单个文本,不应该对单词进行重复计数。
if len(w_list) > self.c_w.shape[1]: # 判断是否在该文本中出现了新的单词
self.c_w = np.concatenate((self.c_w, np.mat(np.zeros((self.c_w.shape[0], len(w_list) - self.c_w.shape[1])))), axis=-1)
# 对c_w矩阵,补加上新单词的位置
self.c_w[c_idex, :] = self.c_w[c_idex, :] + w_list
# 将该i号文本的记录,添加到c_w矩阵的对应行当中
print(i)
self.c_w = np.delete(self.c_w, self.c_w.shape[0] - 1, axis=0)
# 消除最后一行,这是我程序的缺陷之处,c_w有原始的一行,最后去除即可
c_num = np.sum(self.c_w,axis=-1)
p_c_w = np.divide(self.c_w + laplas, np.array(c_num).reshape(-1, 1) + len(self.word_list)*laplas)
# 这个操作叫作拉普拉斯正则化,因为某些单词在一些类别当中根本没出现过,但是,按照
# 朴素贝叶斯的计算方式,有p(w1|c)*p(w2|c)...p(wn|c),若某一个单词w没在c类别当
# 中出现过的话,对应p(w|c)就是0.这是很不合理的事情,我们在文本分类这样的任务当中,
# 不能因为有一些在c当中没有统计到的单词,就完全扼杀了该文本属于该类别的可能。拉普拉斯
# 会使得每一个单词对应的p(w|c)都大于0,同时还保证了所有的p(w|c)相加,概率和仍为1.还
# 有,我们会把概率相乘换成对数相加的形式,因为当一个文本当中的单词过多,多个p(w|c)相乘
# 会得到一个非常小的数,计算机的浮点数据类型都无法准确表示,最终得到0.这显然给我们的
# 最后的比较造成很大的困扰,所以,拉普拉斯正则化十分重要。
p_c = np.divide(np.array(self.c_count), len(labels))
# 每个类别的文本的数量,处以总的文本的数量,获得p(c)即某一类别的文本出现的概率
w_num = np.sum(self.c_w, axis=0)
# 我们对c_w矩阵的每一行进行相加的操作,得到每一个类别统计到的单词数目。统计的方式很
# 考究,单个文本当中的单词,不应该进行重复统计,不同文本的相同单词要重复统计。我们既
# 防范了个别文本过度使用某词语所造成的破坏,也兼顾到了单词出现频率的计量。
p_w = np.divide(w_num, np.sum(w_num))
# 每个单词出现的次数除以总的单词出现次数,这里对单词数量的统计也很考究。我还是建议,单
# 个文本当中的单词,不要重复计量,或者压缩重复计量的比例,除了第一次计量之后,第二次就
# 累加0.1等操作,第三,第四......,我认为,这也是一种不错的方法,这些方法,我都会尝试
# 一下。我们这样操作,将过度使用某单词的影响进行了削减,也实际地考虑到了,过度使用和只
# 使用一次也是有区别的,就比如你在某个文本当中,写了一个like,说明你喜欢,是正面的。而
# 你写了5个like,实际上体现了你特别喜欢,喜欢的程度更深了,对于分类,应该有影响。也有一
# 些am is are, 我们最好不去统计这些单词,我们不重复计量,也是消除这些没有情感的单词的
# 影响,我们可以做一下统计,看这几种方式,是否让这些单词在不同类别之间分布得更加均匀。
# 了。P_w不影响最终的分类结果,因为对于w进行分类的时候,p(w)都是相同的。影响的是p_c
self.p_c_w_log = np.log(p_c_w)
self.p_c_log = np.log(p_c)
self.p_w_log = np.log(p_w)
# 我们把概率值,进行log运算,它不影响我们最终的比较结果,而且计算机能够准确地显示出log
# 函数的运算结果
def predict(self,data):
# 所谓的朴素贝叶斯文本分类器,不过是我们利用训练数据得到的一些变量而已。在分类的
# 时候,也只是使用这些变量,计算p(c1|w),p(c2|w),p(c3|w)...的值,值最大的对应
# 的ci,就是我们要分类的类别。
pwlog = self.p_w_log
word_list = self.word_list
pcwlog = self.p_c_w_log
pclog = self.p_c_log
c_list = self.c_list
sumplogw = np.sum(pwlog)
# 这个值就是log(p(w)),它对于分类结果,没有任何影响,但为了体现模型的完整性,我还是
# 把这一部分的内容给添加上了。
answers = []
# answers用于存放每个样本的分类结果
for i in range(len(data)): # 用于遍历所有的文本,i是文本的标号
str_lower = str.lower((data.iloc[i]))
# 将该文本处理为小写的,为什么要小写呢?因为,大写和小写,在情感的分类上是同等地位
# 我们没有必要再多花一份存储的开销,而且可能导致分类结果的波动,因为大写的单词,在
# 不同的类别的占比可能差异很大,所以把大写改成小写,好处真的很多。不仅仅是节省存储
# 空间,也让我们在对结果分类的时候,分类的结果更加合理,
str_pure = str_lower.translate(str.maketrans('', '', string.punctuation))
# 将文本的标点去除掉
list_ = str_pure.split()
# 以空格来将文本分割成数组
word_vector = np.zeros(len(word_list))
word_cvector = np.zeros(len(word_list))
# 提取该文本的词向量,这里也很考究,是记录是否出现,还是记录出现的次数?还是以
# 0到1的权重来计入词向量。这里,我们也应该采用不同的方法来尝试一下。
for word in list_: # 对该文本对应的数组进行遍历
if word in word_list: # 判断文本当中的单词,是否在单词列表当中
word_index = word_list.index(word)
# 获取单词在单词表当中的位置
word_cvector[word_index] += 1
word_vector[word_index] +=self.generate_weight(word_cvector,word_index)
# 将相应的词向量的位置的值置为1,而不是加1.
word_vector = np.reshape(word_vector, (-1, 1))
# 将词向量的尺寸进行修改,将行向量修改为列向量,方便矩阵的乘法运算
pclog = np.reshape(pclog, (-1, 1))
# 将pclog从行向量修改为列向量
ans0 = (pcwlog * word_vector)
# c*w * w*1 = c*1,我们这样就完成了每个类别的的log(p(w|c))的运算
ans1 = ans0 + pclog
# 完成了log(p(w|c)*p(c))的计算
ans = ans1 - sumplogw
# 我还多此一举地把log(p(w))给捎带上了,它对于结果而言,可有可无,但是,我
# 不是搞工程,我是要分析这项简单技术的细节。
category_belongs = c_list[np.argmax(ans)]
# c*1的列向量,值最大的序号,对应于c_list的相应序号位置的值就是分类的结果
answers.append(category_belongs)
# 将分类的结果添加到answers当中进行记录
print(i)
# 给程序设计师,显示当前的文本位置。
return answers
5 实验结果分析
数据下载链接:百度云盘下载链接
提取码:wmid
代码分享:Github代码共享链接
我们做朴素贝叶斯文本分类模型的初衷,就是希望分类的准确率可以尽可能得高。我制作的朴素贝叶斯模型是针对英文制作的,所以我选择了一个英文的数据源进行实验。
我所做的这个任务是一项二分类的任务,数据集包含训练集和测试集,训练集包含有17150个文本数据,测试集数据包含有7350个文本数据,不重复的单词数量为120090个。这样一个规模的数据集,个人电脑是可以应付得了的。
我设计了8款朴素贝叶斯模型,它们分别是1、以单词为单位进行计数,2、以文本为单位进行计数,3、以y=1-0.1(x-1)(x为单词出现的次数)为权重计数函数进行计数,4、以y=1/x为权重计数函数进行计数。5、以y=e^(1-x)为权重计数函数进行计数6、以除首次计数1,其余计数0.1的方式进行计数。7、以除首次计数1,其余计数0.5的方式进行计数。8、以除首次计数1外,其余计数0.9的方式进行计数。
| accuracy | word | paragraph | 1/x | 1-0.1(x-1) | e^(1-x) | 0.1 | 0.5 | 0.9 |
|---|---|---|---|---|---|---|---|---|
| train_set | 0.9208 | 0.9372 | 0.9332 | 0.9279 | 0.9346 | 0.9358 | 0.9304 | 0.9225 |
| test_set | 0.8434 | 0.8517 | 0.8491 | 0.8460 | 0.8512 | 0.8518 | 0.8468 | 0.8446 |
(表3: 各种单词计量方式在未使用停用词表时的准确率对比)
从实验得到的数据可知,精确到单词的计量方式,它的效果是最差的。所以,当一个文本当中出现了多个相同单词的时候,我们在计数单词的出现次数时,我们最好不要单词出现几次就计数几次。Paragraph作为传统采用的计数方法,达到了非常好的效果。而且设计简单,我推荐大家使用这种计数的方法。以0.1为计数除第一次出现该单词外的计数权重,它在测试集上达到了更好的效果,这隐约给我们一种信号,我们如果额外考虑除第一次外单词出现的情况,我们能够达到更好的效果,我们最好在0到0.1的范围内去考虑权重值。
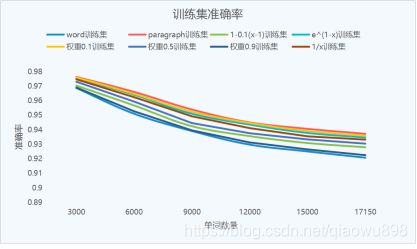

从目前的结果来看的话,我们对于除首次外出现的单词的计数,应该以更小的权重来进行计数。对于除首次出现的单词,大家可以尝试一下以0.05、0.01为权重来进行计数。此时,我们很有可能获得比paragraph模型更好的效果。
在进行文本分类时,停用词的处理也非常重要。它能够让我们的模型更加合理,因为在构建朴素贝叶斯模型的时候,如果数据量不太大的话,一些没有感情含义的单词在不同类别当中的比例很可能不同。那么,如果出现这种情况,这对我们对文本分类是一种干扰。(由于单词’is’这样没有情感成分的单词,它在两个类别当中的比例应该是0.5:0.5,但是由于我们的数据量太小,数据比例难以趋于稳定,可能得到0.45:0.55这样的比例,它对于情感分类也有一定的影响,但是,这是不合理的。而停用词的做法是忽略掉像’is’这样的单词,也即默认是0.5:0.5的比例。而且,使用停用词可以减小我们的计算复杂度,模型的数据规模。可以说是双赢操作!停用词处理,要视情况而定,文本分类是非常适用的。但是,单词预测就要掂量掂量了,最好不要使用停用词处理。)
我增加了停用词表的处理,我们可以对比一下使用停用词表和不使用停用词表之间的区别。
| accuracy | word | paragraph | 1/x | 1-0.1(x-1) | e^(1-x) | 0.1 | 0.5 | 0.9 |
|---|---|---|---|---|---|---|---|---|
| train_set | 0.9357 | 0.9417 | 0.9395 | 0.9378 | 0.9405 | 0.9413 | 0.9389 | 0.9366 |
| test_set | 0.8544 | 0.8558 | 0.8567 | 0.8561 | 0.8574 | 0.8563 | 0.8562 | 0.8546 |
(表2:各种单词计量方式在使用停用词时的准确率对比)
从数据的表现来看,相对于没有使用停用词表的情况,准确率提升了。而且,在测试集当中,新的计量方式的准确率,除了最后一组数据,其余数据均超过了传统的计量方式。这足以说明,我们的模型有着更好的分类效果。


6 总结
至此,我们已经完成了关于朴素贝叶斯模型的大量工作。我对于朴素贝叶斯模型的改变,是基于对于单词的计数规则出发的。欢迎大家提出自己认为合理的计数方式。也十分欢迎大家发表自己的看法。