LeetCode刻意练习30--通配符匹配

题目：
给定一个字符串 (s) 和一个字符模式 § ，实现一个支持 ‘?’ 和 ‘*’ 的通配符匹配。

‘?’ 可以匹配任何单个字符。
‘*’ 可以匹配任意字符串（包括空字符串）。
两个字符串完全匹配才算匹配成功。

说明:
s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 *。

方法一：递归

这道题很容易想到递归算法，我们利用两个变量跟踪我们要匹配的字符串，先匹配第一个字符，如果第一个字符是匹配的，则匹配剩下的字符串。

string	abcde
pattern	a*de

例如我们要看string和pattern是否匹配，则看第一个字符是否匹配，如果是，则匹配剩下的字符串，否则，这两个字符是不匹配的。

string	a	bcde
pattern	a	*de

如何判断一对字符是否匹配呢？

假设 a 是String里的一个字符， b 是pattern里的一个字符，这两个字符匹配的条件是
(1) a=b
(2) b=’?’
(3) b=‘ * ’

上述的条件满足其中一个即可。
（1）（2）很好理解，主要看（3），当pattern里出现 ‘ * ’如何处理。

如果 pattern 里出现 ‘*’

string	bcde
pattern	*de

*可以匹配0-n个字符，所以就是看下列字符串是否匹配：

• 匹配0个字符，pattern去掉一个*，string去掉0个字符

string	bcde
pattern	de

• 匹配1个字符，pattern去掉一个*，string去掉一个字符

string	cde
pattern	de

• 匹配2个字符，pattern去掉一个*，string去掉两个字符

string	de
pattern	de

代码实现如下：

  public boolean isMatch(String s, String p) {
        char[] s1 = s.toCharArray();
        char[] p1 = p.toCharArray();
        return isMatchRecursive(s1, p1, 0, 0);
    }

    public boolean isMatchRecursive(char[] s, char[] p, int i, int j) {
        //如果两个都是“”
        if (j == p.length)
            return i == s.length;

        if (p[j] != '*') {
            //如果两个对应位置两个字符相等，或者p[j]==‘？’
            if (i < s.length && s[i] == p[j] || p[j] == '?')
                return isMatchRecursive(s, p, i + 1, j + 1);
            else {
                return false;
            }
        } else {
            //如果p[j]==‘*’
            //例如**bc,直接跳到最后一个‘*’ "*bc"
            while (j < p.length - 1 && p[j + 1] == '*') {
                j++;
            }

            //计较*ab
            /* 先-1，为了保证可以匹配0个
            */
            i--;
            while (i < s.length) {
                if (isMatchRecursive(s, p, i + 1, j + 1))
                    return true;
                i++;//匹配1个，2个，直到s遍历结束
            }
            return false;
        }
    }

对这个算法进行递归树分析，可以很清楚的看出有许多重叠的子问题，因此特别费时。

方法二：动态规划（自底向上）

一般能够用递归算法的都可以用动态规划解决，动态规划有两种方法，一种是自顶向下（记忆法），一种是自底向上（填表法）。一般自底向上更简洁，更容易理解。

我们先创建一个表格用来记录子字符串是否已经匹配过了。
T[i][j] 的值表示的string[0-i] 和pattern[0-j]是否匹配，如果匹配则存 true，否则 存 false，这是一个bool表。

填表的规则：

1 T[0][0]=true 两个字符均为空字符

2.如果string[ i ]==pattern[ j ], T[i][j]是否匹配取决于前面的字符串T[i-1][j-1]是否匹配。
举个例子：

索引	0	1	2
string	b	a	e
pattern	c	a	d

string[1]==pattern[1]=a,但是因为他们前面的字符串是不匹配的，因此他们也不匹配。

3.如果pattern[ j ]=’?’,T[i][j]是否匹配取决于前面的字符串T[i-1][j-1]是否匹配。
举个例子：

索引	0	1	2
string	b	a	e
pattern	?	a	d

pattern[ j ]=’?’,因为他们前面的字符串是匹配的(都是空），因此他们也匹配。

4.如果pattern[ j ]=’*’,T[i][j]是否匹配取决于前面的字符串T[i][j-1]或者T[i-1][j]是否匹配。

索引	0	1	2	3	4
string	b	a	e	d	e
pattern	b	a	*	e

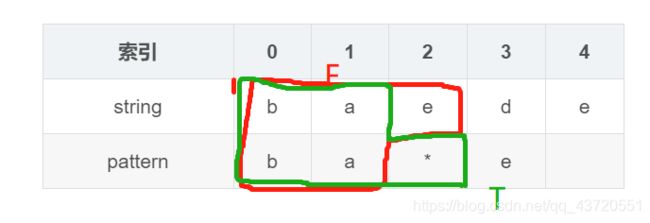
两个的关系是或，因此只要有一个是true，则T[i][j]是true。

5.上述均不符合，则填入F

我们根据上述填表规则举个例子。

string =“baced” 行表头
pattern=“b**a？ed”列表头

代码实现如下：

    public boolean isMatch(String s, String p) {
        char[] str = s.toCharArray();
        char[] pattern = p.toCharArray();

        //replace multiple * with one*
        //e.g a**b***c->a*b*c
        int writeIndex = 0;
        boolean isFirst = true;
        for (int i = 0; i < pattern.length; i++) {
            if (pattern[i] == '*') {
                if (isFirst) {
                    pattern[writeIndex++] = pattern[i];
                    isFirst = false;
                }
            } else {
                pattern[writeIndex++] = pattern[i];
                isFirst = true;
            }
        }
        boolean T[][] = new boolean[str.length + 1][writeIndex + 1];

        T[0][0] = true;

        if (writeIndex > 0 && pattern[0] == '*')
            T[0][1] = true;

        for (int i = 1; i < T.length; i++) {
            for (int j = 1; j < T[0].length; j++) {
                if (pattern[j - 1] == '?' || str[i - 1] == pattern[j - 1])
                    T[i][j] = T[i - 1][j - 1];
                else if (pattern[j - 1] == '*') {
                    T[i][j] = T[i - 1][j] || T[i][j - 1];
                }

            }
        }
        return T[str.length][writeIndex];

    }