Java数据结构 - 数组与ArrayList
数据结构(Java语言描述) - 数组与ArrayList
一、什么是数组
数组是在内存中开辟的一段地址连续且大小相等的内存单元，每个单元存储相同数据类型的值。这些内存单元称之为数组的元素，通过数组的下标（或称索引）访问，下标从0开始。
数组的特点：
- 数组一旦定义其长度就固定。
- 各元素的数据类型相同。
- 通过下标来访问。
二、数组的声明与初始化
语法格式：[访问修饰符] 数据类型[ ] 数组名 = new 数据类型[长度];
int[] nums = new int[10]; //整型数组
String[] strs = new String[5]; //字符串数组
Object[] objects = new Object[3]; //对象数组
数组的初始化分为静态初始化和动态初始化。
1.静态初始化
在声明数组的同时给元素赋值，数组的长度就是元素列表的长度。这种初始化方式适合事先就知道数组的各元素。
//声明长度为0的空数组
int[] nums1 = {}; //省略写法
int[] nums2 = new int[]{}; //完整写法
//字符串数组
String[] names1 = {"Tom","Bob","Jack","Me"};
String[] names2 = new String[]{"Tom","Bob","Jack","Me"};
//对象数组
Employee[] employees = {new Employee("张三",18), new Employee("李四",19)};
Employee[] employees = new Employee[]{new Employee("张三",18), new Employee("李四",19)};
注意：当使用完整写法时，数组的长度不能被指定。
double[] scores = new double[3]{100.0, 98.8, 99}; //错误写法
2.动态初始化
在声明数组时还不知道数组元素该被赋什么值，则使用动态初始化的方式。
//举例：随机生成一百个1~100之间的数字
Random random = new Random();
//先声明数组
int[] nums = new int[100];
//再初始化
for(int i = 0; i < 100; i++){
nums[i] = random.nextInt(100) + 1;
}
三、数组的访问与遍历
语法格式：数组名[下标值] = 指定值;
通过数组下标的访问方式可以对数组元素进行随机读写操作。当下标值超出了数组的长度时，会抛出下标越界异常。
String[] carBrands = new String[5];
carBrands[0] = "劳斯莱斯";
carBrands[1] = "阿斯顿马丁";
carBrands[2] = "法拉利";
carBrands[3] = "布加迪";
carBrands[4] = "兰博基尼";
//carBrands[6] = "五菱宏光"; //会抛ArrayIndexOutOfBoundsException
将数组的所有元素都访问一遍，即是对数组进行遍历。
//将数组各元素值输出到控制台
//方式一：
for(int i = 0; i < 5; i++){
System.out.println(carBrands[i]);
}
//方式二：
for(String s : carBrands){
System.out.println(s);
}
四、数组元素增删改查的时间复杂度
1.查询和修改操作
在数组中，下标是对数组元素进行随机访问的特定手段。如果预先知道要访问的元素位置，则可通过下标直接访问该元素值，时间复杂度为O(1)。而如果不知道访问的元素位置，则需要进行线性查找，逐个进行排除，时间复杂度最坏为O(N)。
2.添加操作
往数组尾端添加元素时，其时间复杂度为O(1)。
往数组首端添加元素时，其时间复杂度为O(N)。
int length = 10;
int[] nums = new int[length]; //声明一个长度为10的数组
for(int i = 0; i < 8; i++){ //给前8个元素赋值
nums[i] = i;
}
//尾端再添加一个元素
nums[8] = 9; //此时是O(1).
//此时再向首端添加一个新元素
//nums[0] = 11; 错误写法！不能直接添加，因为会覆盖掉原有值。
//需要先将数组各元素值整体后移一步，然后再添加
for(int i = length - 1; i > 0; i--){
nums[i] = nums[i - 1];
}
nums[0] = 11; //此时是O(N).
因为尾端添加元素不用移动其他元素，所以为O(1)。而首端添加元素需要先将数组整体后移一步，移动的操作进行了N-1次（N为数组已有元素个数），然后加上添加的操作O(1)，所以是O(N)。
3.删除操作
删除数组尾端元素时，时间复杂度为O(1)。
删除数组首端元素时，时间复杂度为O(N)。
int[] nums = {1,2,3,4,5,6,7,8,9,10};
//删除尾端元素
nums[9] = -1; //这里用-1标志已删除
debug：
尾端删除时不需要做其他操作，所以这里为O(1)。
//删除首端元素
nums[0] = -1;
debug：
这里首端删除操作其实一次就完成了，但为什么说时间复杂度是O(N)呢？
可以这样想，假如我们在食堂排队打饭，当队首的人打完饭离开后，排在后面的人应该整体往前移一步，而不是把走的那个人刚才占的位置一直空着。当第二个人先前走一步、打完饭离开，后面的同学也是按着之前的步骤，先前移一步，然后轮到下一个人。
回到代码中，我现在想继续删0下标上的元素，如果我不把后面元素向前移动的话，就删的还是-1。但是我想删的不是它，所以我得移动其他元素。
//将后面元素整体前移一步
for(int i = 1; i < 9; i++){
nums[i - 1] = nums[i];
}
此时加上N-1次的移动操作，时间复杂度即是O(N)。
平时我们说的时间复杂度一般都指最坏时间复杂度，这里数组的添加和删除操作，最坏情况下都是O(N)。从效率上来讲，这种数据结构的元素增删操作开销比较大，那么有没有一种数据结构能够实现对元素增删操作时间复杂度是O(1)的呢，当然有！链表就可以实现，关于链表的讲解，我们放到下一节。
五、数组存在的弊端和ArrayList的引入
数组的长度一旦指定就无法修改了，且数组没有提供对元素增删改查操作的功能。所以对此，Java提供了ArrayList集合类，此实现类是在数组这种数据结构的基础上提供了操作元素的各种方法，并且可以自动扩容长度。
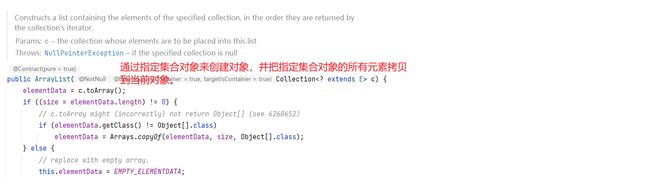
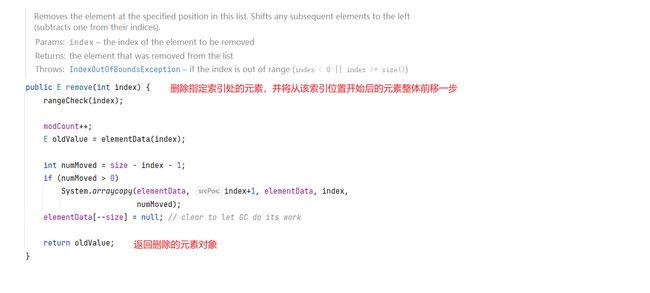
六、ArrayList源码分析
解析该实现类的中的基本结构。
属性字段
构造器
add()方法
自动扩容机制
remove()方法
文章为本人独立编写，难免会有错误之处。
如发现有误，恳请评论提出！