树--二叉树(C语言纯手凹)
目录
目录
1.什么是树?(不深入,仅做了解)
2.树的表示方式
2.1孩子兄弟表示法(左孩子右兄弟)
2.2孩子表示法
2.3双亲表示法
3.什么是二叉树
4.二叉树分类
4.1满二叉树
4.2完全二叉树
4.3二叉搜索树(二叉查找树、二叉排序树)
4.4平衡二叉搜索树(AVL树)
5.二叉树的存储结构
6.二叉树性质
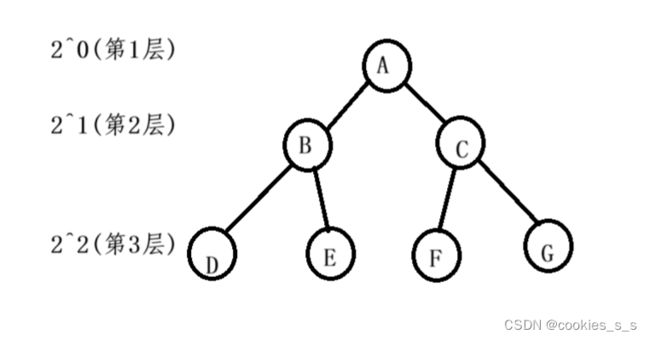
6.1若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点
6.2 若规定根节点的层数为1,则深度为h的二叉树的最大结点数(满二叉)是2^h- 1(等比数列求和)
6.3对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2 +1
(公式记住就好)
6.4 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h = Log 2 (N + 1)(由2取对数可推)
7.二叉树性质相关选择题
7.1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( B )
7.2.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )
7.3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( B )
8.二叉树链式结构的遍历
8.1深度优先遍历
8.2广度优先遍历
9.实现
9.1前序遍历的实现
9.2中序遍历的实现
9.3后序遍历的实现
9.4前中后序遍历有关的选择题
9.5层序遍历(广度优先遍历)的实现
10.有关二叉树的OJ题目
10.1 144. 二叉树的前序遍历 - 力扣(LeetCode)
10.2 94. 二叉树的中序遍历 - 力扣(LeetCode)
10.3 145. 二叉树的后序遍历 - 力扣(LeetCode)
10.4 104. 二叉树的最大深度 - 力扣(LeetCode)
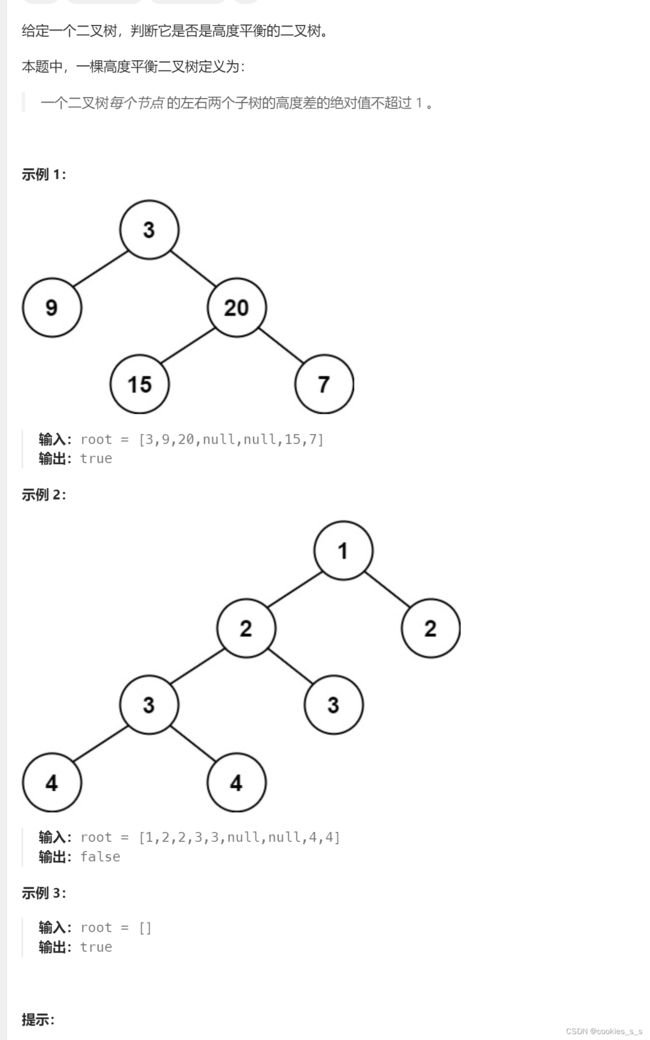
10.5110. 平衡二叉树 - 力扣(LeetCode)
10.6清华大学OJ-二叉树遍历
1.什么是树?(不深入,仅做了解)
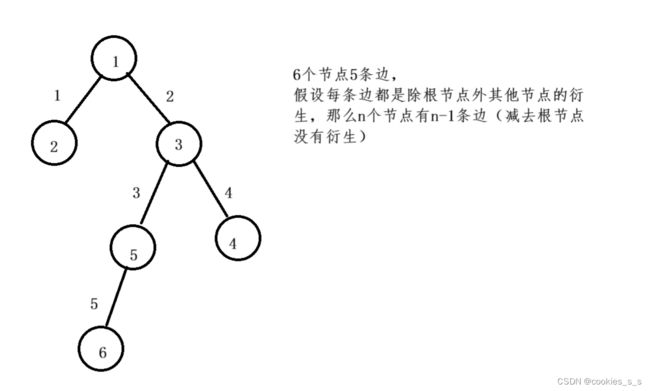
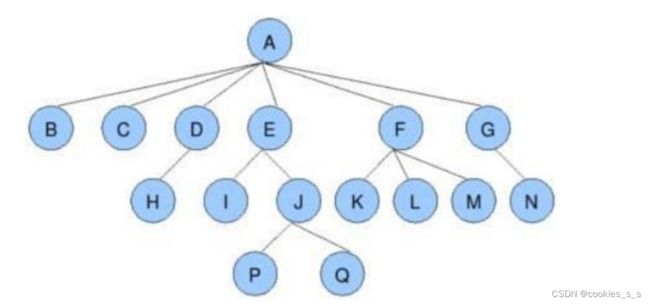
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。 有一个特殊的结点,称为根结点,根节点没有前驱结点,除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继 因此,树是递归定义的。
A为根节点,#为NULL,D、E为叶节点。
判断下面的是不是树?
注意这个是非树,需要知道树的性质:
1.每个节点(除根节点外)有且只有一个父节点
2.子树之间不相连
3.一颗n节点的树有n-1条边
4.0节点为空树
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B 的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节 点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;(也有根为第0层的说法)
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的多颗树的集合称为森林。
2.树的表示方式
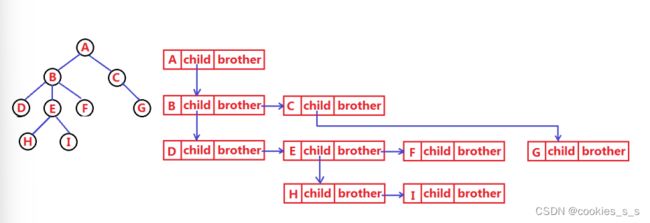
2.1孩子兄弟表示法(左孩子右兄弟)
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子节点
struct Node* _pNextBrother; // 指向其下一个兄弟节点
DataType _data; // 节点数据域
};2.2孩子表示法
typedef int DataType;
struct Node
{
struct Node* _Child1; // 第1个孩子节点
struct Node* _Child2; // 第2个孩子节点
struct Node* _Child3; // 第3个孩子节点
struct Node* _Child4; // 第4个孩子节点
//...(可能有很多个孩子节点)
};
有很多孩子节点就不适用了,一般用于二叉树。
2.3双亲表示法
typedef int DataType;
#define MAXX 100
//树的节点
typedef struct ParentTreeNode
{
DataType data;
int parent;
}PTNode;
//树的定义
typedef struct ParentTree
{
PTNode arr[MAXX];//数组结构
int num;//节点数
}PTree;3.什么是二叉树
二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
特点:
1. 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
2. 二叉树的子树有左右之分,其子树的次序不能颠倒。
4.二叉树分类
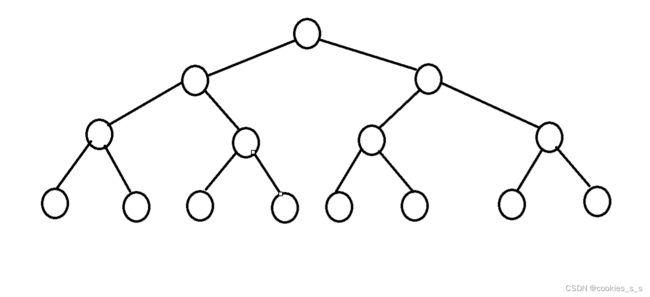
4.1满二叉树
一个二叉树,如果每一个层的结点数都达到最大值(2个),则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1(计算等会讲) ,则它就是满二叉树。
4.2完全二叉树
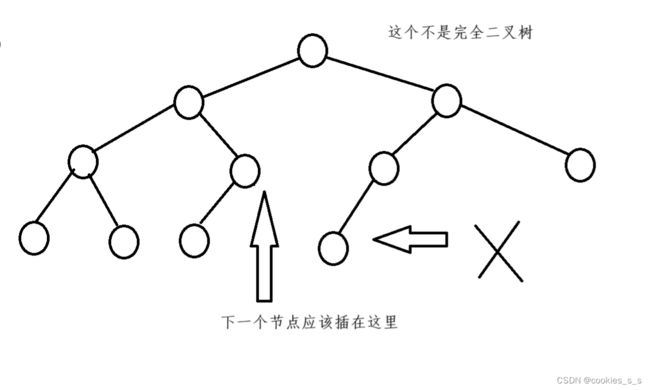
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。除了底层节点可能没填满,其他层每个节点的度都为二叉树最大(2个),并且底层的节点都集中在底层靠左边若干位置(不靠左就不是),若底层为第h层,则最后一层可能有1~2^(h-1)个节点。满二叉树是一种特殊的完全二叉树。
4.3二叉搜索树(二叉查找树、二叉排序树)
二叉搜索树是有数值的,是一个有序树,每个节点满足下列规则:
1.若它的左子树不为空,则左子树上所有节点的值都小于它的根节点的值;(别理解错了,好好理解一下)
2.若它的右子树不为空,则右子树上所有节点的值都大于它的根节点的值;
3.它的左右子树都为二叉搜索树;
总结:左小右大。
4.4平衡二叉搜索树(AVL树)
平衡二叉树又名为AVL树,它可以是空树,或者它的左右两个子树的高度(深度)差的绝对值(abs函数)不超过1,并且左右两个子树都是一颗平衡二叉树。
5.二叉树的存储结构
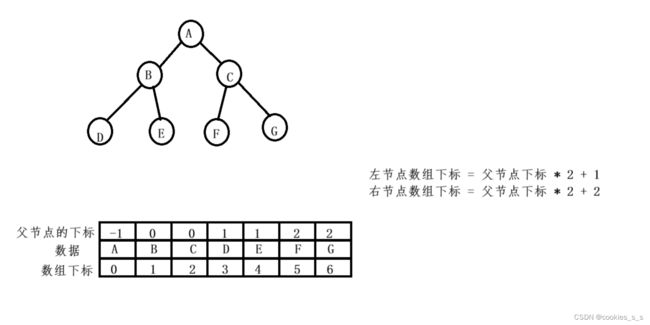
二叉树一般可以使用两种结构存储,一种顺序存储(数组),一种链式存储(指针)
一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,所以一般使用链式存储的方式。
链式存储:
顺序存储(按照树的层次遍历顺序来存储节点)(一般用于堆排序):
leftchild = parent*2 + 1;
rightchild = parent*2 + 2;
parent = (child-1) / 2 (忽略小数点).
6.二叉树性质
6.1若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点
6.2 若规定根节点的层数为1,则深度为h的二叉树的最大结点数(满二叉)是2^h- 1(等比数列求和)
6.3对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2 +1
(公式记住就好)
6.4 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h = Log 2 (N + 1)(由2取对数可推)
7.二叉树性质相关选择题
7.1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( B )
A 不存在这样的二叉树 B 200 C 198 D 199
解析:性质6.3秒了
7.2.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )
A n B n+1 C n-1 D n/2
7.3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( B )
A 11 B 10 C 8 D 12
解析:由题意知道是完全二叉树,估算一下2^9 - 1== 512(满二叉树9层节点数),那么531就要排到10层了,所以B。
8.二叉树链式结构的遍历
二叉树主要有两种遍历方式:深度优先遍历,广度优先遍历。
8.1深度优先遍历
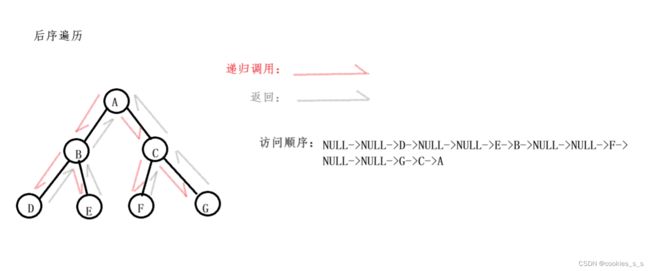
先往深度遍历,遇到子节点时再往回遍历,深度优先遍历又分为 前序遍历(NLR)、中序遍历(LNR)、后序遍历(LRN),N-根,L-根的左子树,R-根的右子树,根节点是必定访问的,所以顺序是根据根节点的访问顺序命名的。
8.2广度优先遍历
设二叉树的 根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问 树的结点的过程就是层序遍历。
9.实现
9.1前序遍历的实现
#include
typedef int DataType;
//树节点
typedef struct TreeNode
{
DataType data;//数据域
struct TreeNode* left;//左子树
struct TreeNode* right;//右子树
}TN;
//构建树
void CreatTree(TN* tree, TN* lefttree, TN* righttree,DataType x)
{
tree->data = x;
tree->left = lefttree;//连接左树
tree->right = righttree;//连接右树
}
//前序遍历//递归实现
void PrefaceTraversal(TN* tree)
{
if (tree == NULL)//临界条件--叶子节点
{
printf("NULL ");
return;
}
printf("%d ", tree->data);//访问根节点
PrefaceTraversal(tree->left);//访问左子树
PrefaceTraversal(tree->right);//访问右子树
}
int main()
{
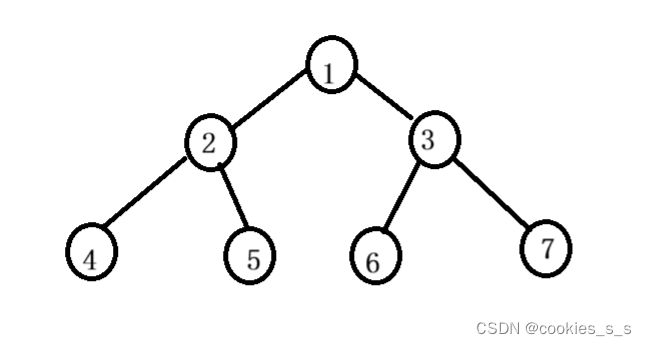
//搭建一颗树
TN tree1,tree2,tree3,tree4,tree5,tree6,tree7;
CreatTree(&tree1, &tree2, &tree3, 1);
CreatTree(&tree2, &tree4, &tree5, 2);
CreatTree(&tree3, &tree6, &tree7, 3);
CreatTree(&tree4, NULL, NULL, 4);
CreatTree(&tree5, NULL, NULL, 5);
CreatTree(&tree6, NULL, NULL, 6);
CreatTree(&tree7, NULL, NULL, 7);
PrefaceTraversal(&tree1);//访问
return 0;
} 9.2中序遍历的实现
//中序遍历//递归实现
void MidTraversal(TN* tree)
{
if (tree == NULL)//临界条件--叶子节点
{
printf("NULL ");
return;
}
MidTraversal(tree->left);//访问左子树
printf("%d ", tree->data);//访问根节点
MidTraversal(tree->right);//访问右子树
}
9.3后序遍历的实现
//后序遍历//递归实现
void PosTraversal(TN* tree)
{
if (tree == NULL)//临界条件--叶子节点
{
printf("NULL ");
return;
}
PosTraversal(tree->left);//访问左子树
PosTraversal(tree->right);//访问右子树
printf("%d ", tree->data);//访问根节点
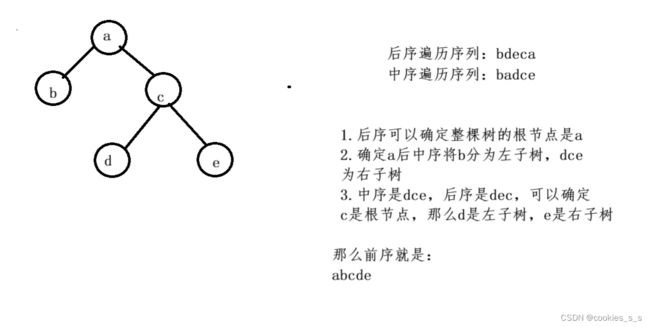
}9.4前中后序遍历有关的选择题
解析:前序和后序可以确定根节点(包括子树的根节点),中序可以根据前面分开的根节点确定左子树和右子树。
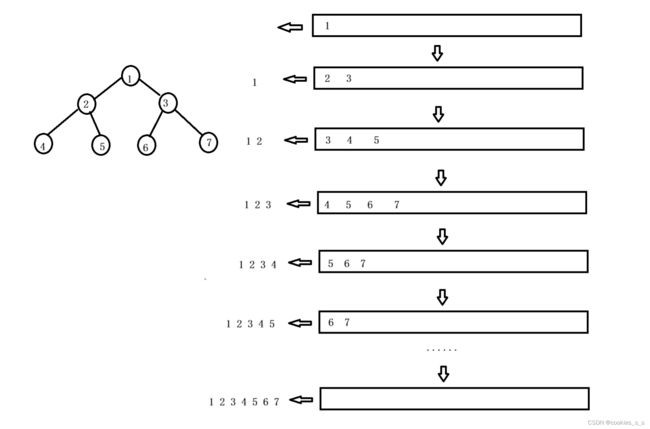
9.5层序遍历(广度优先遍历)的实现
实现原理:使用队列,先进先出;
核心思想:上一层带下一层;
#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#include
typedef int DataType;
typedef struct TreeNode* QDataType;
//树节点
typedef struct TreeNode
{
DataType data;//数据域
struct TreeNode* left;//左子树
struct TreeNode* right;//右子树
}TN;
//构建树
void CreatTree(TN* tree, TN* lefttree, TN* righttree, DataType x)
{
tree->data = x;
tree->left = lefttree;//连接左树
tree->right = righttree;//连接右树
}
//队列节点
typedef struct QueueNode
{
//指向下一个
struct QueueNode* next;
//数据域
QDataType data;//这里数据是树的结构体指针
}QN;
//队列
typedef struct Queue
{
//记录头节点
QN* head;
//记录尾节点
QN* tail;
}Queue;
//初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->head = q->tail = NULL;
}
//入队列--尾插
void QueuePush(Queue* q, QDataType tree)
{
assert(q);
QN* newnode = (QN*)malloc(sizeof(QN));
if (newnode == NULL)//开辟失败
{
perror("malloc fail");
exit(-1);
}
//队列为空
if (q->head == NULL)
{
q->head = q->tail = newnode;
newnode->data = tree;
newnode->next = NULL;
}
//队列不为空
else
{
q->tail->next = newnode;
newnode->data = tree;
newnode->next = NULL;
q->tail = newnode;
}
}
//出队列--头删
void QueuePop(Queue* q)
{
assert(q);
//队列为空不能删
assert(q->head);
//只有一个节点的情况
if (q->head->next == NULL)
{
free(q->head);
q->head = q->tail = NULL;
return;
}
//队列多个节点
QN* temp = q->head->next;
free(q->head);
q->head = temp;
}
//判断队列是否为空
bool QueueEmpty(Queue* q)
{
assert(q);
//空为真
return q->head == NULL;
}
//访问队头
QDataType QueueFront(Queue* q)
{
assert(q);
//空不能访问
assert(q->head);
return q->head->data;
}
//销毁
void QueueDestroy(Queue* q)
{
assert(q);
QN* pcur = q->head;
//循环遍历
while (pcur)
{
QN* temp = pcur->next;
free(pcur);
pcur = temp;
}
//置空
q->head = q->tail = NULL;
}
//层序遍历
void LevelTraversal(TN* tree)
{
Queue q;
QueueInit(&q);
if (tree)
{
QueuePush(&q, tree);
}
while (!QueueEmpty(&q))
{
TN* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
printf("\n");
QueueDestroy(&q);
}
int main()
{
//搭建一颗树
TN tree1, tree2, tree3, tree4, tree5, tree6, tree7;
CreatTree(&tree1, &tree2, &tree3, 1);
CreatTree(&tree2, &tree4, &tree5, 2);
CreatTree(&tree3, &tree6, &tree7, 3);
CreatTree(&tree4, NULL, NULL, 4);
CreatTree(&tree5, NULL, NULL, 5);
CreatTree(&tree6, NULL, NULL, 6);
CreatTree(&tree7, NULL, NULL, 7);
LevelTraversal(&tree1);//访问
return 0;
} 10.有关二叉树的OJ题目
10.1 144. 二叉树的前序遍历 - 力扣(LeetCode)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
//统计节点个数
int TreeSize(struct TreeNode* root){
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//前序遍历
void prevorder(struct TreeNode* root,int* a, int* pi)
{
if(root == NULL)
return;
a[*pi] = (root->val);
(*pi)++;
prevorder(root->left,a,pi);
prevorder(root->right,a,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
//创建数组
int size = TreeSize(root);
int* arr = (int*)malloc(sizeof(int) * size);
int i = 0;
prevorder(root,arr,&i);
*returnSize = size;
return arr;
}10.2 94. 二叉树的中序遍历 - 力扣(LeetCode)
10.3 145. 二叉树的后序遍历 - 力扣(LeetCode)
上面两道做法跟10.1一样
10.4 104. 二叉树的最大深度 - 力扣(LeetCode)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int maxDepth(struct TreeNode* root) {
if(root == NULL)
{
return 0;
}
int left = maxDepth(root->left);
int right = maxDepth(root->right);
return left > right ? left + 1 : right + 1;
}10.5110. 平衡二叉树 - 力扣(LeetCode)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
//深度
int MaxDepth(struct TreeNode* root)
{
if(root == NULL)
return 0;
int left = MaxDepth(root->left);
int right = MaxDepth(root->right);
return left > right ? left + 1 : right + 1;
}
bool isBalanced(struct TreeNode* root) {
if(root == NULL)
return true;
int left = MaxDepth(root->left);
int right = MaxDepth(root->right);
if(abs(left - right) < 2 && isBalanced(root->left) && isBalanced(root->right))//要判断子树本身是否是平衡二叉树
return true;
else
return false;
}
10.6清华大学OJ-二叉树遍历
二叉树遍历__牛客网 (nowcoder.com)
先创建树(分治思想递归构建),再中序遍历。
#include
#include
#define MAXX 100
typedef struct TreeNode
{
struct TreeNode* left;
struct TreeNode* right;
char val;
}TN;
TN* CreatTree(char* s, int* pi)
{
if (s[*pi] == '#')
{
(*pi)++;
return NULL;
}
TN* root = (TN*)malloc(sizeof(TN));
if (root == NULL)
{
perror("malloc fail");
exit(-1);
}
root->val = s[*pi];
(*pi)++;
root->left = CreatTree(s, pi);
root->right = CreatTree(s, pi);
return root;
}
void Inorder(TN* root)
{
if (root == NULL)
{
return;
}
Inorder(root->left);
printf("%c ", root->val);
Inorder(root->right);
}
int main()
{
char s[MAXX];
scanf("%s", s);
int i = 0;
TN* root = CreatTree(s, &i);
Inorder(root);
return 0;
}