代码随想录算法训练营第四天|24. 两两交换链表中的节点 19.删除链表的倒数第N个节点 面试题 160.链表相交 142.环形链表II
24.两两交换链表中的节点
思路:在要交换两个节点的前一个节点设置一个cur指针,并且设置temp1,temp2保存节点再进行互换,当只有奇数个节点则奇数节点和null无需互换;若偶数节点则两两都互换,最后返回head。
细节:while中的判断不能写反,若cur->next->next!=null写在前面,当cur->next指向空指针时会发生空指针异常
代码:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* cur = dummyHead;
ListNode* temp1;//保存cur后面的一个节点
ListNode* temp2;//保存交换节点后的链表
while(cur->next != nullptr && cur->next->next != nullptr){//仅当cur后两个节点不为空,才可进行节点互换
temp1 = cur->next;//1
temp2 = temp1->next->next;//2,temp2保存互换节点后的链表关系,可以防止前面两个节点互换后,链接到后面的链表
cur->next = temp1->next;//3
cur->next->next = temp1;//4
temp1->next = temp2;
cur = temp1;
}
head = dummyHead->next;
return head;
}19.删除链表的倒数第n个节点
思路:双指针法,先移动快指针,移动n个位置,慢指针在虚拟头节点不动,此时慢指针与快指针的距离相差n个位置,可以形象看成一个固定窗口,把快慢指针同时移动到快指针空的位置,慢指针即为倒数第n个节点,但是需要注意的是要删除慢指针指向的节点,必须知道前一个节点,则需要在刚开始移动快指针完毕后,把快指针再往后移动一个位置,则快慢指针同时移动完后,慢指针指向要删除节点的前一个节点,此时删除节点就简单许多。
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* slow = dummyHead;
ListNode* fast = dummyHead;
while(n-- && fast != nullptr){//先移动快指针
fast = fast->next;
}
fast = fast->next;//注,需要提前移动一步
while(fast != nullptr){
fast = fast->next;
slow = slow->next;
}
slow->next = slow->next->next;
return dummyHead->next;
}160.链表相交
题目的题意并不是要比较相同的数值而是指针的地址相同
思路:两个链表长度不一,可以先进行尾部对齐,然后把较长的链表指针移动到较短的指针相同位置再一起移动比较.
代码:
int ListLength(ListNode* head){//根据长度移动节点
int len = 0;
while(head != NULL){
len++;
head = head->next;
}
return len;
}
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = ListLength(headA);
int lenB = ListLength(headB);
if(lenA < lenB){//比较出较长的链表,把长链表跟短链表尾部对齐
int len = lenB-lenA;
while(len--){
headB = headB->next;
}
}
else if(lenA >lenB){
int len = lenA-lenB;
while(len--){
headA = headA->next;
}
}
while(headA != headB){//两链表尾部对齐后一起移动
headA = headA->next;
headB = headB->next;
}
return headA;//符合会返回该指针,不符合会返回null
}142.环形链表||
思路:双指针法
第一步:判断链表是否有环;快慢指针同时从头节点出发,快指针移动两步,慢指针移动一步,当快慢指针相遇则证明有环,否则无环。(若有环,快慢指针为什么一定会相遇?因为若快慢指针同时都移动一步,则两个指针相对而言是不动的,若快指针移动两步,则快指针相对慢指针而言,快指针是一步一步接近慢指针直到相遇的)
第二步:寻找环的入口;
如图2-1,假设把链表中的环围成一个圈,头节点到环的入口距离为x,在环中fast和slow指针相遇的点与环的入口距离为y,再走z的距离可以再回到环的入口。
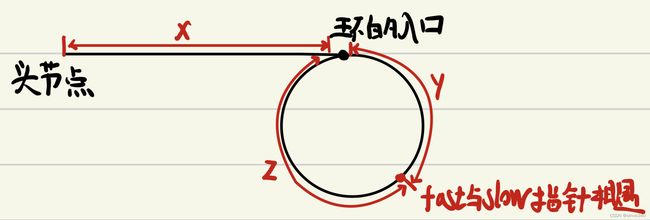 2-1
2-1
fast与slow在环内相遇时,slow的移动距离为x+y,fast由于是先进入环内,当两者相遇肯定是fast追赶slow,所以相遇时fast最少在环内移动了1圈,设圈数为n,且n>=1,fast最少移动了x+y+z+y,整理得fast的移动通式:x+n(y+z)+y;y+z为环一圈的距离。
不难得出2倍的slow移动距离和fast的移动距离相等,得等式:2(x+y)=x+n(y+z)+y,(该等式有个疑问,若n=100,左边=右边?,答案不是的,这步不能简单的进行数学左右值相等理解,因为本题的n虽然有下届,fast与slow在进入环内的第一圈第一会相遇,所以n当且仅当为1)
两边化简得:x=(n-1)(y+z)+z,n>=1
此时又引出个重要问题,fast和slow在环内的第一圈就一定会相遇。why?
 2-2
2-2
如图2-2,把环给铺开成一条直线,fast在环内一定是在追赶slow的,当slow最初进入环内并要在第一圈入口前到达A点,而fast的移动距离是比slow大的,在当slow到达A点时,fast一定会到达B点,在slow-A这段距离中,一定存在一个点使得fast与slow相遇,即得结论,fast与slow在第一圈就会相遇,所以n=1.
再回到公式:x=z,结合2-1图解可得到,在fast和slow相遇后,分别设index1从头节点出发,index2从fast与slow相遇点出发,index1和index2得移动距离是相同的,当两指针相遇时则是环的入口。
代码:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;//fast跳两步
slow = slow->next;//slow跳一步
if(fast == slow){//是否有环
//此时快慢指针相遇,则找环的入口,即把index1和index2一起移动,直到相等,即x=z
ListNode* index1 = fast;
ListNode* index2 = head;
while(index1 != index2){
index1 = index1->next;
index2 = index2->next;
}
return index1;//已经找到环的入口
}
}
return NULL;//无环
}
