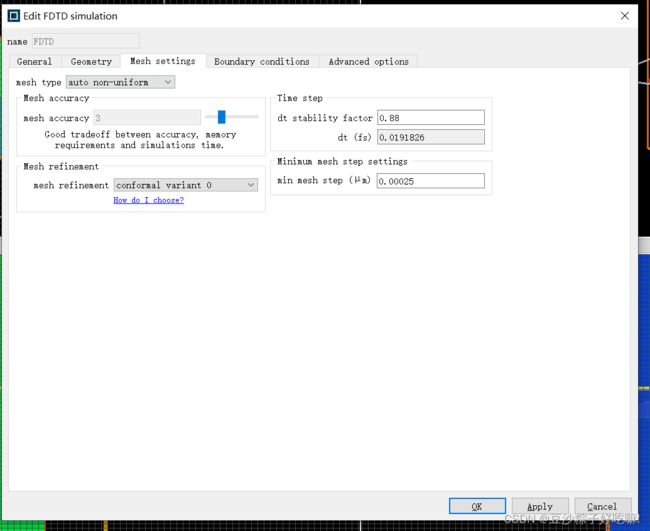
FDTD的稳定性条件及网格设置
时域算法稳定性
时域稳定性
时域有限差分法是依据Yee网格上构造麦克斯韦旋度方程的时域有限差分方程,即以差分方程的解来代替原来电磁场偏微分方程组的解。只有离散后的差分方程组的解是收敛和稳定的,这时,这种代替才有意义。所谓收敛性就是指离散间隔趋近于零时,差分方程的解在空间任意一点和任意时刻都一致趋于原方程的解。稳定性是指寻求一种离散间隔所满足的条件,在此条件下差分方程的数值解和原方程的严格解之间的差为有界。
CFL稳定条件要求时间增量 Δ t \Delta t Δt相对于空间网格小于特定的数值
Δ t ≤ 1 c 1 Δ x 2 + 1 Δ y 2 + 1 Δ z 2 \Delta t \le \frac{1}{c\sqrt{\frac{1}{\Delta x}^2 +\frac{1}{\Delta y}^2+\frac{1}{\Delta z}^2 }} Δt≤cΔx12+Δy12+Δz121
对于正方体网格而言,有
Δ t ≤ Δ x c 3 \Delta t\le \frac{\Delta x}{c\sqrt{3}} Δt≤c3Δx
如对于 10 n m 10 nm 10nm网格而言时间步长应小于0.0193 fs
数值色散
平面电磁波在自由空间中传播时,由于自由空间中, ϵ \epsilon ϵ和 μ \mu μ与频率无关,平面波相速度与频率无关,即无色散。但用时域有限差分法在数值空间模拟这一电磁问题时,算法所模拟的计算网格中的波模式会发生数值色散,也就反应了网格数值中的波模式的相速度与频率有关,因此出现的色散,称之为数值色散。1
为减小数值色散影响,应有
δ m ≤ λ 12 \delta_m\le \frac{\lambda}{12} δm≤12λ
如何设置mesh refinement2
默认的“Conformal Variant 0”设置适合大部分模拟
如果模拟包含金属,推荐使用“Conformal Variant 1”,对于较小的网格尺寸,这种设置可以提供比"staircasing"更好的收敛性,但对于较大的网格尺寸,如 ∣ ϵ p l a s m a > > ∣ ϵ d i e l e c t r i c ∣ |\epsilon_{plasma}>>|\epsilon_{dielectric}| ∣ϵplasma>>∣ϵdielectric∣时效果不佳。
mesh refinement 特点
Staircasing(阶梯式):
对Yee网格中的每个位置进行材料评估,确定其所属的材料类型,并在该位置仅使用单一材料属性计算E场。
这种离散化结构无法精确处理发生在单个Yee单元内的结构变化,因此产生的介电常数网格呈现出与笛卡尔网格吻合的“阶梯状”特征。
任何层结构都会被近似到Yee单元格上最接近的E场位置,这意味着层厚度分辨率无法优于dx。
Conformal Variants:
Lumerical的共形网格技术(CMT)利用Maxwell积分方程在两种材料界面附近的严密物理描述,能够整合Lumerical的多系数材料。
CMT能够处理任意色散介质之间的界面。
通常情况下,这种方法能以给定的网格尺寸提供更高的精度,或是在不降低精度的前提下显著加快模拟速度,由于模拟时间与网格尺寸成(1/dx)^4的关系,结果往往能在大约1/10的时间内得出。
共形网格化有三种方式:
Conformal Variant 0:不对涉及金属或PEC材料的界面应用CMT。
Conformal Variant 1:对所有材料(包括PEC和金属)均应用CMT。
Conformal Variant 2:对涉及金属和PEC的界面采用Yu-Mittra方法1,而对其他所有界面应用CMT。
共形网格技术能够在给定的网格尺寸下提升模拟精度,或者在不牺牲精度的前提下显著加快计算速度。由于模拟时间与网格尺寸存在1/dx^4的关系,采用共形网格技术后,通常可以在大约原本十分之一的时间内得出结果。此外,CMT(共形网格技术)对几何参数变化具有子网格级别的敏感性,极大地便利了设计优化过程。
Dielectric Volume Average(介质体积平均法):
只适用于处理Yee单元格中一个或多个介电材料之间的界面,此时生成的是各介电常数在该单元格内的简单体积平均值作为平均介电常数。
用户指定的“细化级别”N将决定在2D中将单元格划分为NxN子单元,在3D中划分为NxNxN子单元来计算体积平均。
若非介电材料位于单元格中心,则对该特定单元格回归使用阶梯法。尽管此方法没有严格的物理依据,但可用于低介电常数对比度的介电结构。
Volume Average(体积平均法):
每个单元格的介电常数是单元格内两种材料介电常数的简单体积平均值。每种材料可以具有完全色散特性。
如果在一个单元格中发现超过两种材料,则对该单元格同样回归使用阶梯法。
Yu-Mittra方法1:
Yu和Mittra提出此方法用于提高PEC/介电界面建模时的精度。Lumerical的实现是对原始Yu-Mittra公式的微小扩展,可应用于任意色散介质。
在考虑PEC存在时,通过只包含PEC外部且电场非零区域(C1)来调整轮廓积分C。在Lumerical的实现中,在更新B场时,轮廓C1在材料1中求解,而轮廓C2 = (C-C1)在材料2中求解。当其中一种材料为PEC(E=0)时,这与PEC适用的原始Yu-Mittra公式相同。
若在一个单元格中检测到超过两种材料,则也对该单元格使用阶梯法。
Yu-Mittra method 1:
Yu和Mittra提出的方法旨在解决在模拟理想电导体(PEC)与介电材料界面时提高计算精度的问题。这种方法特别适用于处理电磁场问题中由于PEC的特性(即内部电场为零)导致的经典数值方法失效的情况。
在原始的Yu-Mittra方法中,当存在PEC时,在进行场求解相关的积分运算时,特别是与磁感应强度B场更新相关的积分路径C,会将积分区域调整为仅包含PEC外部且电场非零的区域(记为C1)。这样可以更准确地描述PEC边界条件对周围介质的影响。
Lumerical对该方法进行了扩展,使其能够适应任意色散介质的情况。具体实施时,假设单元格内有两种材料,当更新B场时,分别对两种材料内的轮廓积分进行评估:
在材料1中的积分路径采用C1;
而在材料2中的积分路径则采用C2 = (C-C1),即扣除已经考虑过的PEC外部区域后剩余的部分。
若单元格中的一种材料是PEC,则其内部电场E=0,此时Lumerical实现的算法便与原始Yu-Mittra针对PEC的方法完全一致。
然而,如果在一个单一网格单元(cell)内检测到超过两种材料,则该单元将不适用Yu-Mittra方法1或其他高级处理方式,而是退化回使用较为简单的阶梯法(Staircasing)进行近似处理。
该方法能够提高模拟弯曲PEC表面时的精度。这种方法实现简单,能够精确描述电磁辐射在微波和射频频率下与大多数金属材料的相互作用。然而,在光学频率下的许多类型模拟中,如传播通过多层分散材料堆叠时,它可能无法提供准确的结果。

Yu-Mittra method 2:
Yu和Mittra提出的第二种方法旨在提高对介电材料界面建模时的精度,特别适用于处理具有复杂介电结构的情况。Lumerical对该方法进行了扩展,使其同样适应任意色散介质。在Yee网格单元内,根据每种介电材料所占据网格步长的比例,为每个介电常数分量分配一个有效的介电常数。若在一个单一网格单元内检测到超过两种材料,则该单元会退回到使用阶梯法进行近似处理。
Precise Volume Average:
精确体积平均法应用于光子逆向设计中,虽然内存需求较高,但能够提供对几何微小变化最敏感的网格化处理,这是逆向设计中准确梯度计算所必需的。相比于常规的体积平均法,这种方法通过更精确的技术来确定网格单元内两种材料比例下的平均介电常数。
基于FDTD的二维超材料的电磁器件仿真与设计 ↩︎
electing the best mesh refinement option in the FDTD simulation object ↩︎