详解并查集(最详细的解释)

并查集

并查集的作用：

1：将两个集合合并成一个集合

2：询问两个元素是否在同一个集合中

存储的方式：

我们用树的形式来维护所有的集合，每个集合用一颗树来表示

树中根节点的编号就是该集合的编号

用一个$fa[]$数组来存储每一个点的父亲结点

问题：

如何判断树根？$x=fa[x]$;

如何判断每一个点所在的集合编号 $while(x!=fa[x])x=fa[x]$;

如何合并两个集合？将一个集合的根节点的父亲指向另外一个集合的根节点

px是x集合的编号，py是y集合的编号，将两个集合合并就是 $fa[px]=py$

路径压缩：如果我们需要寻找这个点所在集合的根节点，我们从当前点开始沿着父亲节点一直往上面找，当我们找到根节点的时候，我们就将走的过程中经过的所有点指向根节点。通过这个操作的过程，我们就完全可以将时间复杂度直接将为$O(1)$​​，

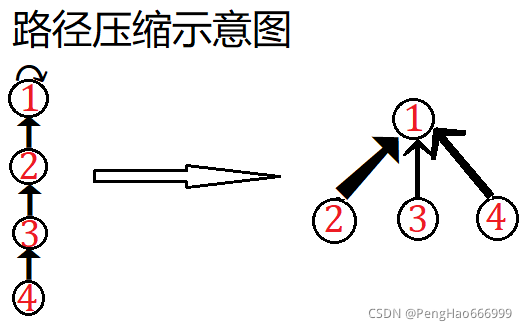
注意：我们做题时运用并查集题目一般都是每次维护时该集合的根节点，可以用根节点来表示集合里面最大值，每一次在合并两个集合的时候通过维护根节点来找到最大值。

代码过程

1：初始化

初始的时候每一个数都是一个集合，所以每一个点的父亲节点就是他自己。

2：并查集的核心操作（返回x所在的集合编号，就是返回根节点的编号）+路径压缩

首先判断该点是否是根节点，如果不是的话，那么就沿着父亲结点走寻找父亲结点的根节点。

void init() {
	for (int i = 1; i <= n; i++)fa[i] = i;
}

int find(int x) {//返回x所在集合的根节点+路径压缩
	if (fa[x] != x)fa[x] = find(fa[x]);
	return fa[x];
}

如何判断两个点是否在一个连通块当中，如果两个点a,b;如果点a可以走到点b，点b也可以走到点a，就说这两个点是连通的。

3：我们如何能够快速求出每一个集合里面的元素呢？答案就是用一个$size[]$​数组（注意只有$size[根节点]$​​才是正确答案，集合里面的元素我们每次更新的是根节点）,初始的时候我们每一个集合里面就只有一个元素，然后，当我们两个元素属于同一个集合的时候，我们就不需要操作，否则，（注意，每一个集合里面的元素我们使用size[根节点]来维护的），所以我们只需要在合并的时候将合并集合的元素个数加到被合并的集合里面即可。

并查集的代码

#include
using namespace std;

const int N = 100010;
int fa[N], size1[N];//fa[N]用来存放每一个结点的父亲结点，size1[N]表示每个集合里面的元素个数
int n, m;

void init() {
	for (int i = 1; i <= n; i++) {
		fa[i] = i;
		size1[i] = 1;
	}
}
int find(int x) {
	if (fa[x] != x)fa[x] = find(fa[x]);
	return fa[x];
}

int main() {
	cin >> n >> m;
	init();
	while (m--) {
		char op;
		cin >> op;
		if (op == 'C') {
			int a, b;
			cin >> a >> b;
			if (find(a) == find(b))continue;//如果两个数在同一个集合中，就不用操作了
			size1[b] += size1[a];//更新集合里面的元素
			fa[find(a)] = find(b);
		}
		else if (op == '1') {
			int a, b;
			cin >> a >> b;
			if (find(a) == find(b))cout << "yes" << endl;
			else cout << "no" << endl;
		}
		else {
			int a;
			cin >> a;
			cout << size1[find(a)] << endl;
		}
	}
	return 0;
}
/*5 5
C 1 2
1 1 2
2 1
C 2 5
2 5*/

例题

题目描述

在一个幼儿园里面有$n$个小朋友，分别编号$1,2,...,n$ 。在这些小朋友中有一些小朋友互为朋友关系，总共有$m$对朋友。
作为幼儿园老师，你想买一些糖果分给小朋友，你知道第$i$个小朋友想要至少$a[i]$个糖果，否则他就会不开心。
同时，如果一个小朋友得到的糖果数小于他某个朋友得到的糖果数，他也会不开心。
请问你最少买多少糖果才能保证每个小朋友都不会不开心呢？

输入描述:

第一行以空格分隔的两个整数$n,m$。
第二行以空格分隔的$n$个正整数$a[i]$。
接下来$m$行每行以空格分隔的两个正整数$u,v$，代表$u$是$v$的朋友，$v$是$u$的朋友。
1≤$n$≤$10^6$
0≤$m$≤$10^6$
1≤$a[i]$≤$10^9$
1≤$u,v$≤$n$,$v$≤$n$,$u$≠$v$

输出描述:

购买的最少糖果数以保证每个小朋友都不会不开心。

示例1

输入

3 1
1 2 3
1 2

输出

7

说明

给第三个小朋友买3个糖果，前两个小朋友都买2两个糖果，总共至少买7个糖果。注意如果给第一个小朋友只买了1个糖果，那么他在看到自己的好朋友2有2个糖果的情况下，他就会不开心。

AC代码

#include
#include
using namespace std;

typedef long long ll;
const int N=1e6+10;
int fa[N],siz[N];
ll a[N];
int n,m;

void init(){
    for(int i=1;i<=n;i++){
        fa[i]=i;
        //siz[i]=1;
    }
}
int find(int x){
    if(fa[x]!=x) fa[x]=find(fa[x]);
    return fa[x];
}

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);
    
    cin>>n>>m;
    init();
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    while(m--){
        int u,v;
        cin>>u>>v;
        if(find(u)==find(v))continue;
        if(a[find(u)]>a[find(v)])swap(u,v);
        fa[find(u)]=find(v);
        //siz[find(v)]+=siz[find(u)];
    }
    ll sum=0;
    for(int i=1;i<=n;i++)sum+=a[find(i)];
    cout<<sum<<endl;
    return 0;
}