【深度学习】数据归一化/标准化 Normalization/Standardization

目录

一、实际问题

二、归一化 Normalization

三、归一化的类型

1. Min-max normalization (Rescaling)

2. Mean normalization

3.Z-score normalization (Standardization)

4.非线性归一化

4-1 对数归一化

4-2 反正切函数归一化

4-3 小数定标标准化（Demical Point Normalization）

四、如何选择归一化函数？

五、Java实现归一化工具类

---

一、实际问题

在数据分析、深度学习中，经常需要对数据进行处理，数据处理时，会发现一个问题：

不同维度的数据，数据范围偏差比较大，如

• 距离地铁的距离——房价的关系
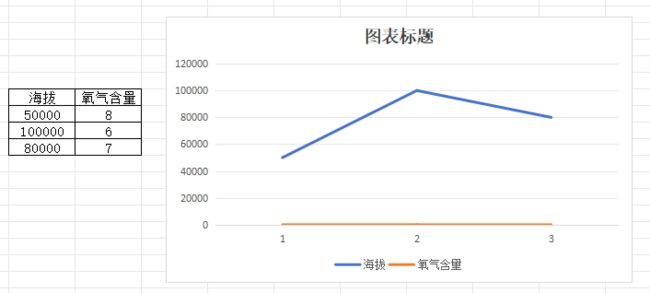
• 海拔高度——氧气含量的关系

一个维度的数据范围大，一个小，导致以下问题：

【1】求解过程不平缓、函数收敛慢

【2】相关性展示不明显

如下图：

海拔越高、氧气含量越低，因为数据范围的原因，导致两者的相关性展示得不明显。

解决得方式就是归一化和标准化

二、归一化 Normalization

归一化，指将数据样本中的数据进行处理，使它们处于同一量级。

如 [0,1] 或者 [-1,1] 或者其它

归一化后，数据更具有可比性，如图

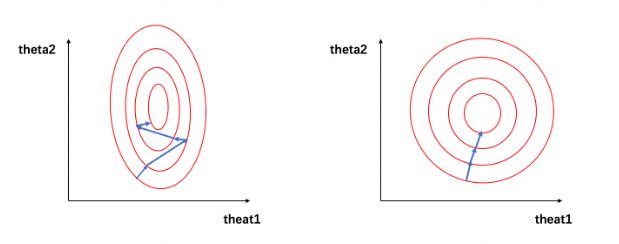
函数的求解过程也会比较平缓，更快求得最优解，如下图

左：未归一化的求解  右：归一化后的求解

三、归一化的类型

1. Min-max normalization (Rescaling)

最值归一化，公式如下：

归一化后的数据范围为 [0, 1]，其中min max分别求样本数据的最小值和最大值。

2. Mean normalization

均值归一化，公式如下：

归一化后的数据范围为 [-1, 1]，其中mean、min、max为样本数据的平均值、最小值和最大值。

3.Z-score normalization (Standardization)

标准差归一化，也成为标准化（标准化其实就是归一化的一种），公式如下：

归一化后的数据范围为实数集，其中mean、σ 分别为样本数据的均值和标准差。

4.非线性归一化

4-1 对数归一化

4-2 反正切函数归一化

归一化后的数据范围为 [-1, 1]

4-3 小数定标标准化（Demical Point Normalization）

j为使

 

的最小整数，归一化后的数据范围为 [-1, 1]

四、如何选择归一化函数？

Min-Max归一化、Mean归一化适合：

【1】最大最小值明确不变：如图像处理中，RGB值为0~255，可以使用Min-Max来处理。

【2】对数据范围有明确要求：如需要数据范围为-1~1

不适合：

【1】最大最小值不明确：每次有新的值加入，之前的结果就会发生改变，导致不稳定。

【2】有过大或过小的异常值存在：效果会较差

Z-score归一化适合：

【1】存在异常值、最大最小值不固定

缺点是：

【1】改变了数据的状态分布，但不会改变分布的种类：经过处理的数据呈均值为0，标准差为1的分布

非线性归一化适合：

【1】数据分化程度较大的场景

五、Java实现归一化工具类

package com.potato.commonpro.util.math;

import java.util.ArrayList;
import java.util.List;

/**
 * 数据样本归一化工具类
 * 包含了多个归一化函数,提供了List/Array两种类型的输入输出，具体的归一化函数如下：
 * 【1】min-max normalization（Rescaling）
 * 【2】mean normalization
 * 【3】Z-score normalization (Standardization)
 * 【4】对数归一化
 * 【5】反正切函数归一化
 * 【6】小数定标标准化
 * 

 * Author:PotatoChan
 * Date:2023-12-30
 */
public class PotatoNormalization {


    /**
     * min-max normalization（Rescaling）
     * 归一化公式：x'=(x-min）/（max-min)
     * 归一化后的数据范围为 [0, 1]，其中min 、max 分别求样本数据的最小值和最大值。
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static List normalizationForMinToMax(List data) {
        List result = new ArrayList<>();
        //求取样本数据中的最大值与最小值
        double max = Double.MIN_VALUE;
        double min = Double.MAX_VALUE;
        for (Double item : data) {
            if (item > max) max = item;
            if (item < min) min = item;
        }
        //计算归一化后的数据
        double dis = max - min;
        for (Double item : data) {
            double num = (item - min) / dis;
            result.add(num);
        }
        return result;
    }

    /**
     * min-max normalization（Rescaling）
     * 归一化公式：x'=(x-min）/（max-min)
     * 归一化后的数据范围为 [0, 1]，其中min 、max 分别求样本数据的最小值和最大值。
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static double[] normalizationForMinToMax(double[] data) {
        double[] result = new double[data.length];

        //求取样本数据中的最大值与最小值
        double max = Double.MIN_VALUE;
        double min = Double.MAX_VALUE;
        for (Double item : data) {
            if (item > max) max = item;
            if (item < min) min = item;
        }
        //计算归一化后的数据
        double dis = max - min;
        for (int i = 0; i < data.length; i++) {
            result[i] = (data[i] - min) / dis;
        }

        return result;
    }

    /**
     * mean normalization
     * 归一化公式：x'=(x-mean）/（max-min)
     * 归一化后的数据范围为 [-1, 1]，其中mean为样本数据的平均值,min 、max 分别求样本数据的最小值和最大值
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static List normalizationForMean(List data) {
        List result = new ArrayList<>();
        //求取样本数据中的最大值与最小值、平均值
        double max = Double.MIN_VALUE;
        double min = Double.MAX_VALUE;
        double mean = 0;
        for (Double item : data) {
            if (item > max) max = item;
            if (item < min) min = item;
            mean += item;
        }
        mean = mean / data.size();

        //计算归一化后的数据
        double dis = max - min;
        for (Double item : data) {
            double num = (item - mean) / dis;
            result.add(num);
        }
        return result;
    }

    /**
     * mean normalization
     * 归一化公式：x'=(x-mean）/（max-min)
     * 归一化后的数据范围为 [-1, 1]，其中mean为样本数据的平均值,min 、max 分别求样本数据的最小值和最大值
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static double[] normalizationForMean(double[] data) {
        double[] result = new double[data.length];
        //求取样本数据中的最大值与最小值、平均值
        double max = Double.MIN_VALUE;
        double min = Double.MAX_VALUE;
        double mean = 0;
        for (Double item : data) {
            if (item > max) max = item;
            if (item < min) min = item;
            mean += item;
        }
        mean = mean / data.length;

        //计算归一化后的数据
        double dis = max - min;
        for (int i = 0; i < data.length; i++) {
            result[i] = (data[i] - mean) / dis;
        }
        return result;
    }

    /**
     * Z-score normalization (Standardization)
     * 归一化公式：x'=(x-mean）/σ
     * 归一化后的数据范围为实数集，其中μ、σ 分别为样本数据的均值和标准差
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static List normalizationForZScore(List data) {
        List result = new ArrayList<>();
        //求取样本数据中的平均值
        double mean = 0;
        for (Double item : data) {
            mean += item;
        }
        mean = mean / data.size();

        //计算方差
        double variance = 0;
        for (Double item : data) {
            variance += (item - mean) * (item - mean);
        }
        variance = variance / data.size();
        //计算标准差
        double standardDeviation = Math.sqrt(variance);

        //计算归一化后的数据
        for (Double item : data) {
            double num = (item - mean) / standardDeviation;
            result.add(num);
        }
        return result;
    }

    /**
     * Z-score normalization (Standardization)
     * 归一化公式：x'=(x-mean）/σ
     * 归一化后的数据范围为实数集，其中μ、σ 分别为样本数据的均值和标准差
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static double[] normalizationForZScore(double[] data) {
        double[] result = new double[data.length];
        //求取样本数据中的平均值
        double mean = 0;
        for (Double item : data) {
            mean += item;
        }
        mean = mean / data.length;

        //计算方差
        double variance = 0;
        for (Double item : data) {
            variance += (item - mean) * (item - mean);
        }
        variance = variance / data.length;
        //计算标准差
        double standardDeviation = Math.sqrt(variance);

        //计算归一化后的数据
        for (int i = 0; i < data.length; i++) {
            result[i] = (data[i] - mean) / standardDeviation;
        }
        return result;
    }

    /**
     * 对数归一化
     * 归一化公式：x'=ln(x)/ln(max)
     * 其中，max为数据样本的最大值
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static List normalizationForlg(List data) {
        List result = new ArrayList<>();
        //求取样本数据中的最大值
        double max = Double.MIN_VALUE;
        for (Double item : data) {
            if (item > max) max = item;
        }
        //计算归一化后的数据
        for (Double item : data) {
            double num = Math.log10(item) / Math.log10(max);
            result.add(num);
        }
        return result;
    }

    /**
     * 对数归一化
     * 归一化公式：x'=ln(x)/ln(max)
     * 其中，max为数据样本的最大值
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static double[] normalizationForlg(double[] data) {
        double[] result = new double[data.length];
        //求取样本数据中的最大值
        double max = Double.MIN_VALUE;
        for (Double item : data) {
            if (item > max) max = item;
        }
        //计算归一化后的数据
        for (int i = 0; i < data.length; i++) {
            result[i] = Math.log10(data[i]) / Math.log10(max);

        }
        return result;
    }

    /**
     * 反正切函数归一化
     * 归一化公式：x'=arctan(x)*(2/PI)
     * 归一化后的数据范围为 [-1, 1],PI表示圆周率Π
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static List normalizationForArctan(List data) {
        List result = new ArrayList<>();
        //计算归一化后的数据
        for (Double item : data) {
            double num = Math.atan(item) * (2 / Math.PI);
            result.add(num);
        }
        return result;
    }


    /**
     * 反正切函数归一化
     * 归一化公式：x'=arctan(x)*(2/PI)
     * 归一化后的数据范围为 [-1, 1],PI表示圆周率Π
     *
     * @param data 数据样本
     * @return 归一化后的数据样本
     */
    public static double[] normalizationForArctan(double[] data) {
        double[] result = new double[data.length];
        //计算归一化后的数据
        for (int i = 0; i < data.length; i++) {
            result[i] = Math.atan(data[i]) * (2 / Math.PI);
        }
        return result;
    }


}